【精品试卷】中考数学一轮复习 专题测试-13 二次函数（基础）（教师版） 12页

专题 13 二次函数（专题测试-基础） 学校:___________姓名：___________班级：___________考号：___________ 一、选择题（共 12 小题，每小题 4 分，共 48 分） 1．（2019·山东中考模拟）已知学校航模组设计制作的火箭的升空高度 h(m)与飞行时间 t(s)满足函数表达式 h ＝－t2＋24t＋1.则下列说法中正确的是( ) A．点火后 9 s和点火后 13 s的升空高度相同 B．点火后 24 s火箭落于地面 C．点火后 10 s的升空高度为 139 m D．火箭升空的最大高度为 145 m 【答案】D 【解析】 A、当 t=9时，h=136；当 t=13时，h=144；所以点火后 9s和点火后 13s的升空高度不相同，此选项错误； B、当 t=24时 h=1≠0，所以点火后 24s火箭离地面的高度为 1m，此选项错误； C、当 t=10时 h=141m，此选项错误； D、由 h=-t2+24t+1=-（t-12）2+145知火箭升空的最大高度为 145m，此选项正确； 故选：D． 2．（2019·东港区日照街道三中中考模拟）将抛物线 y= 1 2 x2﹣6x+21向左平移 2个单位后，得到新抛物线的 解析式为（ ） A．y= 1 2 （x﹣8）2+5 B．y= 1 2 （x﹣4）2+5 C．y= 1 2 （x﹣8）2+3 D．y= 1 2 （x﹣4）2+3 【答案】D 【详解】 y= 1 2 x2﹣6x+21 = 1 2 （x2﹣12x）+21 = 1 2 [（x﹣6）2﹣36]+21 = 1 2 （x﹣6）2+3， 故 y= 1 2 （x﹣6）2+3，向左平移 2个单位后， 得到新抛物线的解析式为：y= 1 2 （x﹣4）2+3． 故选 D． 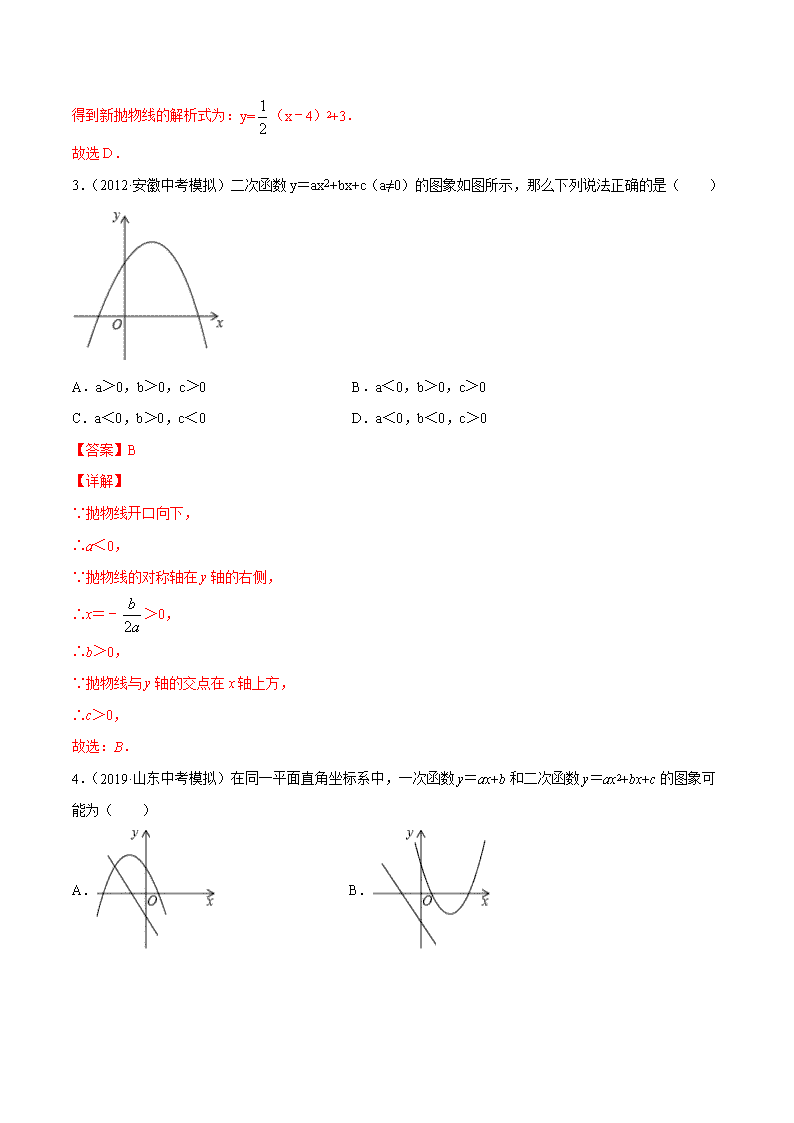3．（2012·安徽中考模拟）二次函数 y＝ax2+bx+c（a≠0）的图象如图所示，那么下列说法正确的是（ ） A．a＞0，b＞0，c＞0 B．a＜0，b＞0，c＞0 C．a＜0，b＞0，c＜0 D．a＜0，b＜0，c＞0 【答案】B 【详解】 ∵抛物线开口向下， ∴a＜0， ∵抛物线的对称轴在 y轴的右侧， ∴x＝﹣ 2 b a ＞0， ∴b＞0， ∵抛物线与 y轴的交点在 x轴上方， ∴c＞0， 故选：B． 4．（2019·山东中考模拟）在同一平面直角坐标系中，一次函数 y＝ax+b和二次函数 y＝ax2+bx+c的图象可 能为（ ） A． B． C． D． 【答案】A 【详解】 A、由抛物线可知，a＜0，x=﹣ 2 b a ＜0，得 b＜0，由直线可知，a＜0，b＜0，故本选项正确； B、由抛物线可知，a＞0，由直线可知，a＜0，故本选项错误； C、由抛物线可知，a＞0，x=﹣ 2 b a ＞0，得 b＜0，由直线可知，a＞0，b＞0，故本选项错误； D、由抛物线可知，a＞0，由直线可知，a＜0，故本选项错误． 故选：A． 5．（2019·甘肃中考模拟）已知函数 y=(k-1)x2-4x+4的图象与 x轴只有一个交点,则 k的取值范围是( ) A．k≤2且 k≠1 B．k<2且 k≠1 C．k=2 D．k=2或 1 【答案】D 【详解】 当 k-1=0，即 k=1时，函数为 y=-4x+4，与 x轴只有一个交点； 当 k-1≠0，即 k≠1时，由函数与 x轴只有一个交点可知， ∴△=（-4）2-4（k-1）×4=0， 解得 k=2， 综上可知 k的值为 1或 2， 故选 D． 6．（2019·黑龙江中考模拟）将抛物线 y=x2先向左平移 2个单位，再向下平移 3个单位后所得抛物线的解 析式为（ ） A．y=（x﹣2）2+3 B．y=（x﹣2）2﹣3 C．y=（x+2）2+3 D．y=（x+2）2﹣3 【答案】D 【详解】 解：抛物线 y=x2的顶点坐标为（0，0），把点（0，0）先向左平移 2个单位，再向下平移 3个单位得到对应 点的坐标为（-2，-3），所以平移后的抛物线解析式为 y=（x+2）2-3． 故选：D． 7．（2019·安徽中考模拟）当 a≤x≤a+1时，函数 y=x2-2x+1 的最小值为 1，则 a的值为（ ） A．-1 B．2 C．0或 2 D．-1或 2 【答案】D 【解析】 当 y=1时，有 x2-2x+1=1， 解得：x1=0，x2=2． ∵当 a≤x≤a+1时，函数有最小值 1， ∴a=2或 a+1=0， ∴a=2或 a=-1， 故选 D． 8．（2018·安徽中考模拟）某农产品市场经销一种销售成本为 40元的水产品．据市场分析，若按每千克 50 元销售，一个月能售出 500千克；销售单价每涨一元，月销售量就减少 10千克．设销售单价为每千克 x元， 月销售利润为 y元，则 y与 x的函数关系式为（ ） A．y＝（x﹣40）（500﹣10x） B．y＝（x﹣40）（10x﹣500） C．y＝（x﹣40）[500﹣10（x﹣50）] D．y＝（x﹣40）[500﹣10（50﹣x）] 【答案】C 【解析】 设销售单价为每千克 x元，此时的销售数量为  500 10 50x  ，每千克赚的钱为 40,x  则    40 500 10 50y x x      . 故选 C. 9．（2019·辽宁中考模拟）点 P1(－1，y1)，P2(3，y2)，P3(5，y3)均在二次函数 y=－x2＋2x＋c的图象上，则 y1，y2，y3的大小关系是( ) A．y3>y2>y1 B．y3>y1=y2 C．y1>y2>y3 D．y1=y2>y3 【答案】D 【详解】 ∵y=-x2+2x+c， ∴对称轴为 x=1， P2（3，y2），P3（5，y3）在对称轴的右侧，y随 x的增大而减小， ∵3＜5， ∴y2＞y3， 根据二次函数图象的对称性可知，P1（-1，y1）与（3，y1）关于对称轴对称， 故 y1=y2＞y3， 故选：D． 10．（2019·湖北中考模拟）下列对二次函数 y=x2﹣x的图象的描述，正确的是（ ） A．开口向下 B．对称轴是 y轴 C．经过原点 D．在对称轴右侧部分是下降的 【答案】C 【详解】A、∵a=1＞0，∴抛物线开口向上，选项 A不正确； B、∵﹣ 1 2 2 b a  ，∴抛物线的对称轴为直线 x= 1 2 ，选项 B不正确； C、当 x=0时，y=x2﹣x=0，∴抛物线经过原点，选项 C正确； D、∵a＞0，抛物线的对称轴为直线 x= 1 2 ， ∴当 x＞ 1 2 时，y随 x值的增大而增大，选项 D不正确， 故选 C． 11．（2018·天津中考模拟）如图，抛物线 y=ax2+bx+3（a≠0）的对称轴为直线 x=1，如果关于 x的方程 ax2+bx ﹣8=0（a≠0）的一个根为 4，那么该方程的另一个根为（ ） A．﹣4 B．﹣2 C．1 D．3 【答案】B 【解析】 ∵关于 x的方程 2 8 0ax bx   有一个根为 4， ∴抛物线 2 8y ax bx   与 x轴的一个交点为（4，0）， 抛物线  2 3 0y ax bx a    的对称轴为直线 1x  ， 抛物线 2 8y ax bx   的对称轴也是 x=1， ∴抛物线与 x轴的另一个交点为  2 0 ，， ∴方程的另一个根为 2x   ． 故选 B． 12．（2019·许昌实验中学中考模拟）如图是二次函数 2y=ax +bx+c的部分图象，由图象可知不等式 2ax +bx+c<0的解集是（ ） A． 15 C． x< 1 且 x>5 D．x＜－1或 x＞5 【答案】D 【解析】 利用二次函数的对称性，可得出图象与 x轴的另一个交点坐标，结合图象可得出 2ax +bx+c<0的解集： 由图象得：对称轴是 x=2，其中一个点的坐标为（5，0）， ∴图象与 x轴的另一个交点坐标为（－1，0）。 由图象可知： 2ax +bx+c<0的解集即是 y＜0的解集， ∴x＜－1或 x＞5。故选 D。 二、填空题（共 5 小题，每小题 4 分，共 20 分） 13．（2016·四川中考真题）设 m，n是一元二次方程 x2＋2x－7＝0的两个根，则 m2＋3m＋n＝_______. 【答案】5 【解析】 根据根与系数的关系可知 m+n=﹣2，又知 m是方程的根，所以可得 m2+2m﹣7=0，最后可将 m2+3m+n变成 m2+2m+m+n，最终可得答案． ∵设 m、n是一元二次方程 x2+2x﹣7=0的两个根， ∴m+n=﹣2， ∵m是原方程的根， ∴m2+2m﹣7=0，即 m2+2m=7， ∴m2+3m+n=m2+2m+m+n=7﹣2=5 14．（2018·湖南中考模拟）某菜农搭建了一个横截面为抛物线的大棚，尺寸如图，若菜农身高为 1.8m，他 在不弯腰的情况下，在棚内的横向活动范围是__m． 【答案】3 【详解】 设抛物线的解析式为：y=ax2+b， 由图得知：点（0，2.4），（3，0）在抛物线上， ∴ ，解得： ， ∴抛物线的解析式为：y=﹣ x2+2.4， ∵菜农的身高为 1.8m，即 y=1.8， 则 1.8=﹣ x2+2.4， 解得：x= （负值舍去） 故他在不弯腰的情况下，横向活动范围是：3米， 故答案为：3． 15．（2018·四川中考真题）如图是抛物线型拱桥，当拱顶离水面 2m时，水面宽 4m，水面下降 2m，水面宽 度增加______m. 【答案】4 2 -4 【详解】 建立平面直角坐标系，设横轴 x通过 AB，纵轴 y通过 AB中点 O且通过 C点，则通过画图可得知 O为原点， 抛物线以 y轴为对称轴，且经过 A，B两点，OA和 OB可求出为 AB的一半 2米，抛物线顶点 C坐标为  0,2 . 通过以上条件可设顶点式 2 2y ax  ，其中 a可通过代入 A点坐标  2,0 . 代入到抛物线解析式得出： 0.5a   ，所以抛物线解析式为 20.5 2y x   ， 当水面下降 2米，通过抛物线在图上的观察可转化为： 当 2y   时，对应的抛物线上两点之间的距离，也就是直线 2y   与抛物线相交的两点之间的距离， 可以通过把 2y   代入抛物线解析式得出： 22 0.5 2x    ，解得： 2 2x   ， 所以水面宽度增加到4 2米，比原先的宽度当然是增加了 4 2 4. 故答案是： 4 2 4. 16．（2013·贵州中考真题）已知二次函数 y=x2+2mx+2，当 x＞2时，y的值随 x值的增大而增大，则实数 m 的取值范围是 ． 【答案】m≥﹣2 【解析】 抛物线的对称轴为直线 2mx m 2 1      ， ∵当 x＞2时，y的值随 x值的增大而增大， ∴﹣m≤2，解得 m≥﹣2。 17．（2019·江苏中考模拟）抛物线的部分图象如图所示，则当 y＞0时，x的取值范围是_____． 【答案】 1 x 3   . 【详解】 ∵抛物线与 x轴的一个交点坐标为（﹣1，0）， 而抛物线的对称轴为直线 x＝1， ∴抛物线与 x轴的另一个交点坐标为（3，0）， ∴当﹣1＜x＜3时，y＞0． 故答案为﹣1＜x＜3． 三、解答题（共 4 小题，每小题 8 分，共 32 分） 18．（2019·辽宁中考模拟）某厂家生产一种新型电子产品，制造时每件的成本为 40元，通过试销发现，销 售量 (y 万件 )与销售单价 (x 元 )之间符合一次函数关系，其图象如图所示．  1 求 y与 x的函数关系式；  2 物价部门规定：这种电子产品销售单价不得超过每件 80元，那么，当销售单价 x定为每件多少元时， 厂家每月获得的利润  w 最大？最大利润是多少？ 【答案】（1） 2 280y x   ；（2）当销售单价 x定为每件 80元时，厂家每月获得的利润  w 最大，最大 利润是 4800元． 【详解】 解：  1 设 y与 x的函数关系式为  0y kx b k   ， 函数图象经过点  40,200 和点  60,160 ， 40 200 60 160 k b k b      ，解得： 2 280 k b      ， y 与 x的函数关系式为 2 280y x   ．  2 由题意得：    2 240 2 280 2 360 11200 2( 90) 5000w x x x x x            ． 试销期间销售单价不低于成本单价，也不高于每千克 80元，且电子产品的成本为每千克 40元， 自变量 x的取值范围是 40 80x  ． 2 0  ， 当 90x  时，w随 x的增大而增大， 80x  时，w有最大值， 当 80x  时， 4800w  ， 答：当销售单价 x定为每件 80元时，厂家每月获得的利润  w 最大，最大利润是 4800元． 19．（2014·山东中考真题）已知二次函数 y＝x2－4x＋3. (1)用配方法求其图象的顶点 C的坐标，并描述该函数的函数值随自变量的增减而变化的情况； (2)求函数图象与 x轴的交点 A，B的坐标，及△ABC的面积． 【答案】（1）顶点 C的坐标是（2，-1），当 x＜2时，y随 x的增大而减少；当 x＞2时，y随 x的增大而增 大；（2）1. 【解析】 试题分析：本题考查了抛物线与 x轴的交点，二次函数的性质，二次函数的三种形式 （1）配方后求出顶点坐标即可； （2）求出 A、B的坐标，根据坐标求出 AB、CD，根据三角形面积公式求出即可． 解：(1)y＝x2－4x＋3＝x2－4x＋4－4＋3＝(x－2)2－1，所以顶点 C的坐标是(2，－1)，当 x≤2时，y随 x的增 大而减小；当 x＞2时，y随 x的增大而增大； (2)解方程 x2－4x＋3＝0得 x1＝3，x2＝1，即 A点的坐标是(1，0)，B点的坐标是(3，0)．如图，过点 C作 CD⊥AB于点 D.∵AB＝2，CD＝1，∴S△ABC＝ AB×CD＝ ×2×1＝1. 20．（2019·安徽中考模拟）某公司投入研发费用 80万元（80万元只计入第一年成本），成功研发出一种产 品．公司按订单生产（产量=销售量），第一年该产品正式投产后，生产成本为 6元/件．此产品年销售量 y （万件）与售价 x（元/件）之间满足函数关系式 y=﹣x+26． （1）求这种产品第一年的利润W1（万元）与售价 x（元/件）满足的函数关系式； （2）该产品第一年的利润为 20万元，那么该产品第一年的售价是多少？ （3）第二年，该公司将第一年的利润 20万元（20万元只计入第二年成本）再次投入研发，使产品的生产 成本降为 5元/件．为保持市场占有率，公司规定第二年产品售价不超过第一年的售价，另外受产能限制， 销售量无法超过 12万件．请计算该公司第二年的利润W2至少为多少万元． 【答案】（1）W1=﹣x2+32x﹣236；（2）该产品第一年的售价是 16元；（3）该公司第二年的利润W2至少为 18万元． 【详解】 （1）W1=（x﹣6）（﹣x+26）﹣80=﹣x2+32x﹣236． （2）由题意：20=﹣x2+32x﹣236． 解得：x=16， 答：该产品第一年的售价是 16元． （3）由题意：7≤x≤16， W2=（x﹣5）（﹣x+26）﹣20=﹣x2+31x﹣150， ∵7≤x≤16， ∴x=7时，W2有最小值，最小值=18（万元）， 答：该公司第二年的利润W2至少为 18万元． 21．（2019·新疆中考模拟）如图，已知二次函数 21 2 y x bx c    的图象经过  2,0A ，  0, 6B  两点． （1）求这个二次函数的解析式； （2）设该二次函数的对称轴与 x轴交于点C，连接 BA， BC，求 ABC 的面积． 【答案】见解析 【详解】 （1）把  2,0A ，  0, 6B  代入 21 2 y x bx c    得 2 2 0 6 b c c        ， 解得 4 6 b c     . ∴这个二次函数解析式为 21 4 6 2 y x x    . （2）∵抛物线对称轴为直线 4 4 12 2 x          ， ∴C的坐标为  4,0 ， ∴ 4 2 2AC OC OA     ， ∴ 1 1 2 6 6 2 2ABCS AC OB       .