2020年辽宁省锦州市中考数学试卷【含答案；word版本试题；可编辑】 11页

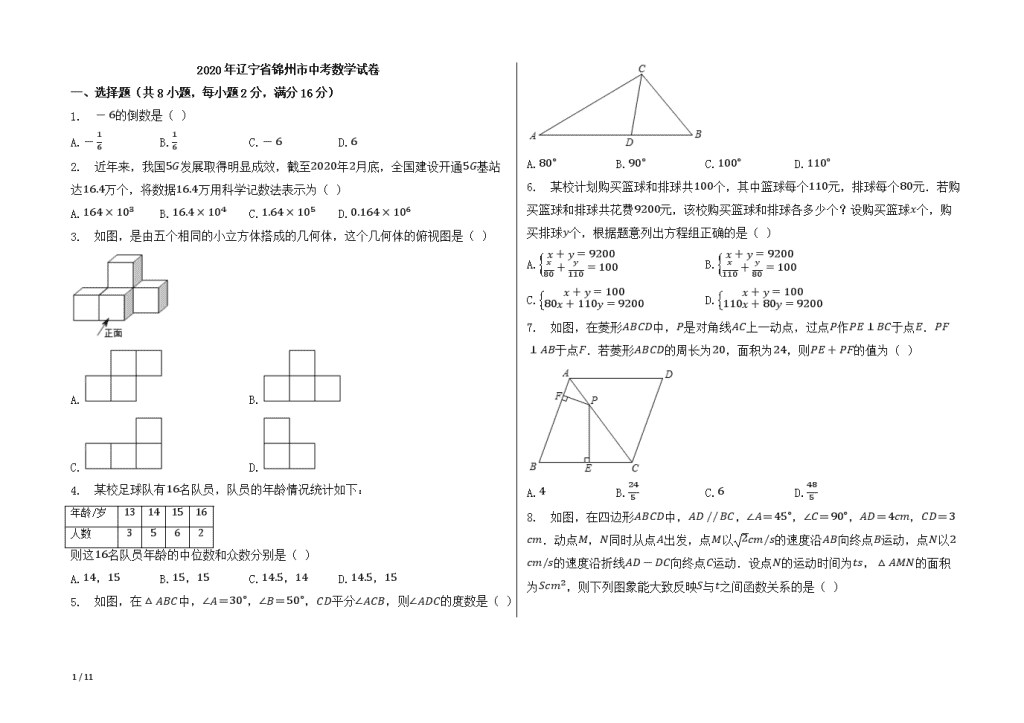
‎2020年辽宁省锦州市中考数学试卷 一、选择题（共8小题，每小题2分，满分16分）‎ ‎1. ‎-6‎的倒数是（ ）‎ A.‎-‎‎1‎‎6‎ B.‎1‎‎6‎ C.‎-6‎ D.‎‎6‎ ‎2. 近年来，我国‎5G发展取得明显成效，截至‎2020‎年‎2‎月底，全国建设开通‎5G基站达‎16.4‎万个，将数据‎16.4‎万用科学记数法表示为（ ）‎ A.‎164×‎‎10‎‎3‎ B.‎16.4×‎‎10‎‎4‎ C.‎1.64×‎‎10‎‎5‎ D.‎‎0.164×‎‎10‎‎6‎ ‎3. 如图，是由五个相同的小立方体搭成的几何体，这个几何体的俯视图是（ ）‎ A. B.‎ C. D.‎ ‎4. 某校足球队有‎16‎名队员，队员的年龄情况统计如下：‎ 年龄/岁 ‎13‎ ‎14‎ ‎15‎ ‎16‎ 人数 ‎3‎ ‎5‎ ‎6‎ ‎2‎ 则这‎16‎名队员年龄的中位数和众数分别是（ ）‎ A.‎14‎，‎15‎ B.‎15‎，‎15‎ C.‎14.5‎，‎14‎ D.‎14.5‎，‎‎15‎ ‎5. 如图，在‎△ABC中，‎∠A＝‎30‎‎∘‎，‎∠B＝‎50‎‎∘‎，CD平分‎∠ACB，则‎∠ADC的度数是（ ）‎ A.‎80‎‎∘‎ B.‎90‎‎∘‎ C.‎100‎‎∘‎ D.‎‎110‎‎∘‎ ‎6. 某校计划购买篮球和排球共‎100‎个，其中篮球每个‎110‎元，排球每个‎80‎元．若购买篮球和排球共花费‎9200‎元，该校购买篮球和排球各多少个？设购买篮球x个，购买排球y个，根据题意列出方程组正确的是（ ）‎ A.x+y=9200‎x‎80‎‎+y‎110‎=100‎‎ ‎ B.‎x+y=9200‎x‎110‎‎+y‎80‎=100‎ C.x+y=100‎‎80x+110y=9200‎‎ ‎ D.‎x+y=100‎‎110x+80y=9200‎ ‎7. 如图，在菱形ABCD中，P是对角线AC上一动点，过点P作PE⊥BC于点E．PF⊥AB于点F．若菱形ABCD的周长为‎20‎，面积为‎24‎，则PE+PF的值为（ ）‎ A.‎4‎ B.‎24‎‎5‎ C.‎6‎ D.‎‎48‎‎5‎ ‎8. 如图，在四边形ABCD中，AD // BC，‎∠A＝‎45‎‎∘‎，‎∠C＝‎90‎‎∘‎，AD＝‎4cm，CD＝‎3cm．动点M，N同时从点A出发，点M以‎2‎cm/s的速度沿AB向终点B运动，点N以‎2cm/s的速度沿折线AD-DC向终点C运动．设点N的运动时间为ts，‎△AMN的面积为Scm‎2‎，则下列图象能大致反映S与t之间函数关系的是（ ）‎ ‎ 11 / 11‎ A. B.‎ C. 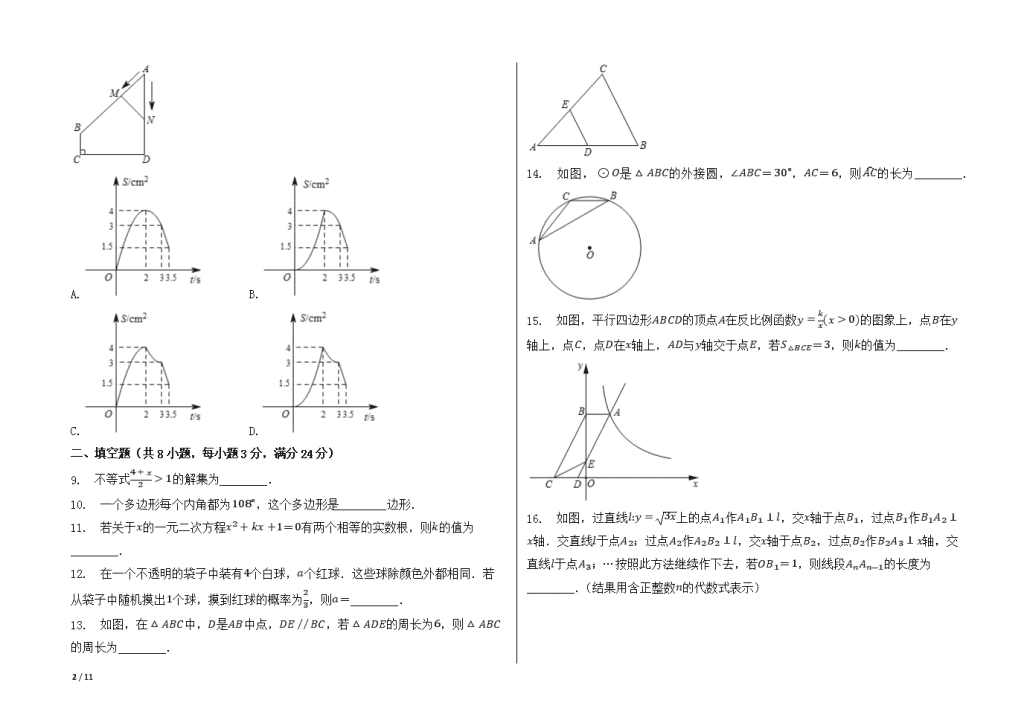D.‎ 二、填空题（共8小题，每小题3分，满分24分）‎ ‎9. 不等式‎4+x‎2‎‎>1‎的解集为________．‎ ‎10. 一个多边形每个内角都为‎108‎‎∘‎，这个多边形是________边形．‎ ‎11. 若关于x的一元二次方程x‎2‎‎+kx+1‎＝‎0‎有两个相等的实数根，则k的值为________．‎ ‎12. 在一个不透明的袋子中装有‎4‎个白球，a个红球．这些球除颜色外都相同．若从袋子中随机摸出‎1‎个球，摸到红球的概率为‎2‎‎3‎，则a＝________．‎ ‎13. 如图，在‎△ABC中，D是AB中点，DE // BC，若‎△ADE的周长为‎6‎，则‎△ABC的周长为________．‎ ‎14. 如图，‎⊙O是‎△ABC的外接圆，‎∠ABC＝‎30‎‎∘‎，AC＝‎6‎，则AC的长为________．‎ ‎15. 如图，平行四边形ABCD的顶点A在反比例函数y=kx(x>0)‎的图象上，点B在y轴上，点C，点D在x轴上，AD与y轴交于点E，若S‎△BCE＝‎3‎，则k的值为________．‎ ‎16. 如图，过直线l:y=‎‎3x上的点A‎1‎作A‎1‎B‎1‎‎⊥l，交x轴于点B‎1‎，过点B‎1‎作B‎1‎A‎2‎‎⊥x轴．交直线l于点A‎2‎；过点A‎2‎作A‎2‎B‎2‎‎⊥l，交x轴于点B‎2‎，过点B‎2‎作B‎2‎A‎3‎‎⊥x轴，交直线l于点A‎3‎；…按照此方法继续作下去，若OB‎1‎＝‎1‎，则线段AnAn-1‎的长度为________．（结果用含正整数n的代数式表示）‎ ‎ 11 / 11‎ 三、解答题（共9小题，满分0分）‎ ‎17. 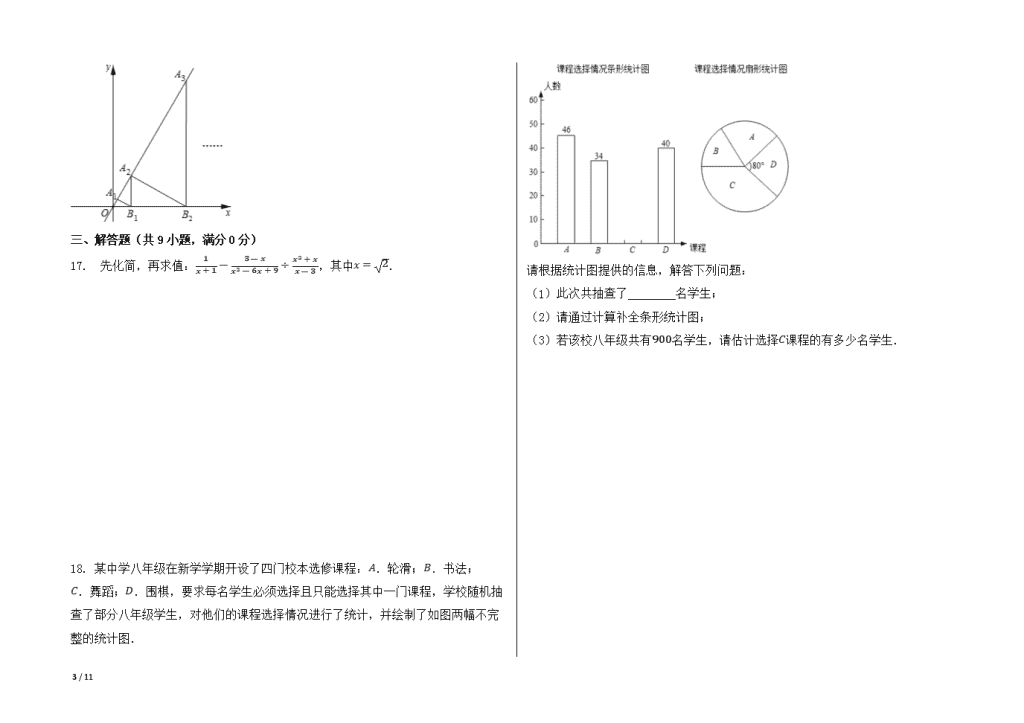先化简，再求值：‎1‎x+1‎‎-‎3-xx‎2‎‎-6x+9‎÷‎x‎2‎‎+xx-3‎，其中x=‎‎2‎．‎ ‎18. 某中学八年级在新学学期开设了四门校本选修课程：A．轮滑；B．书法；C．舞蹈；D．围棋，要求每名学生必须选择且只能选择其中一门课程，学校随机抽查了部分八年级学生，对他们的课程选择情况进行了统计，并绘制了如图两幅不完整的统计图．‎ 请根据统计图提供的信息，解答下列问题：‎ ‎（1）此次共抽查了________名学生；‎ ‎（2）请通过计算补全条形统计图；‎ ‎（3）若该校八年级共有‎900‎名学生，请估计选择C课程的有多少名学生．‎ ‎ 11 / 11‎ ‎19. A，B两个不透明的盒子里分别装有三张卡片，其中A盒里三张卡片上分别标有数字‎1‎，‎2‎，‎3‎，B盒里三张卡片上分别标有数字‎4‎，‎5‎，‎6‎，这些卡片除数字外其余都相同，将卡片充分摇匀．‎ ‎（1）从A盒里班抽取一张卡、抽到的卡片上标有数字为奇数的概率是________；‎ ‎（2）从A盒，B盒里各随机抽取一张卡片，请用列表或画树状图的方法，求抽到的两张卡片上标有的数字之和大于‎7‎的概率．‎ ‎20. 某帐篷厂计划生产‎10000‎顶帐篷，由于接到新的生产订单，需提前‎10‎天完成这批任务，结果实际每天生产帐篷的数量比计划每天生产帐篷的数量增加了‎25%‎，那么计划每天生产多少顶帐篷？‎ ‎21. 如图，某海岸边有B，C两码头，C码头位于B码头的正东方向，距B码头‎40‎海里．甲、乙两船同时从A岛出发，甲船向位于A岛正北方向的B码头航行，乙船向位于A岛北偏东‎30‎‎∘‎方向的C码头航行，当甲船到达距B码头‎30‎海里的E处时，乙船位于甲船北偏东‎60‎‎∘‎方向的D处，求此时乙船与C码头之间的距离．（结果保留根号）‎ ‎22. 如图，‎▱ABCD的对角线AC，BD交于点E，以AB为直径的‎⊙O经过点E，与AD交于点F，G是AD延长线上一点，连接BG，交AC于点H，且‎∠DBG=‎1‎‎2‎∠BAD．‎ ‎ 11 / 11‎ ‎（1）求证：BG是‎⊙O的切线；‎ ‎（2）若CH＝‎3‎，tan∠DBG=‎‎1‎‎2‎，求‎⊙O的直径．‎ ‎23. 某水果超市以每千克‎20‎元的价格购进一批樱桃，规定每千克樱桃售价不低于进价又不高于‎40‎元，经市场调查发现，樱桃的日销售量y（千克）与每千克售价x（元）满足一次函数关系，其部分对应数据如下表所示：‎ 每千克售价x（元）‎ ‎…‎ ‎25‎ ‎30‎ ‎35‎ ‎…‎ 日销售量y（千克）‎ ‎…‎ ‎110‎ ‎100‎ ‎90‎ ‎…‎ ‎（1）求y与x之间的函数关系式；‎ ‎（2）该超市要想获得‎1000‎的日销售利润，每千克樱桃的售价应定为多少元？‎ ‎（3）当每千克樱桃的售价定为多少元时，日销售利润最大？最大利润是多少？‎ ‎24. 已知‎△AOB和‎△MON都是等腰直角三角形‎(‎2‎‎2‎OA-2‎ ‎10.五 ‎11.‎‎±2‎ ‎12.‎‎8‎ ‎13.‎‎12‎ ‎14.‎‎2π ‎15.‎‎6‎ ‎16.‎‎3×‎‎2‎‎2n-5‎ 三、解答题（共9小题，满分0分）‎ ‎17.原式‎=‎1‎x+1‎-‎3-x‎(x-3‎‎)‎‎2‎×‎x-3‎x(x+1)‎ ‎=‎1‎x+1‎+‎‎1‎x(x+1)‎ ‎=xx(x+1)‎+‎‎1‎x(x+1)‎ ‎=‎x+1‎x(x+1)‎ ‎=‎‎1‎x‎．‎ 当x=‎‎2‎时，原式‎=‎1‎‎2‎=‎‎2‎‎2‎．‎ ‎18.‎‎180‎ C项目的人数为‎180-46-34-40‎＝‎60‎（名）‎ 条形统计图补充为：‎ 估计全校选择C课程的学生有‎900×‎60‎‎180‎=300‎（名）．‎ ‎19.‎‎2‎‎3‎ 画树状图得：‎ 共有‎9‎种等可能的结果，抽到的两张卡片上标有的数字之和大于‎7‎的有‎3‎种情况，‎ ‎ 11 / 11‎ ‎∴ 两次两次抽取的卡片上数字之和是奇数的概率为‎3‎‎9‎‎=‎‎1‎‎3‎．‎ ‎20.计划每天生产‎200‎顶帐篷 ‎21.乙船与C码头之间的距离为‎(30‎3‎-40)‎海里．‎ ‎22.证明：∵ AB为‎⊙O的直径，‎ ‎∴ ‎∠AEB＝‎90‎‎∘‎，‎ ‎∴ ‎∠BAE+∠ABE＝‎90‎‎∘‎，‎ ‎∵ 四边形ABCD为平行四边形，‎ ‎∴ 四边形ABCD为菱形，‎ ‎∴ ‎∠BAE=‎1‎‎2‎∠BAD，‎ ‎∵ ‎∠DBG=‎1‎‎2‎∠BAD．‎ ‎∴ ‎∠BAE＝‎∠DBG，‎ ‎∴ ‎∠DBG+∠ABE＝‎90‎‎∘‎，‎ ‎∴ ‎∠ABG＝‎90‎‎∘‎，‎ ‎∴ BG是‎⊙O的切线；‎ ‎∵ ‎∠ABG＝‎∠AEB＝‎90‎‎∘‎，‎∠HAB＝‎∠BAE，‎ ‎∴ ‎△ABH∽△AEB，‎ ‎∴ AB‎2‎＝AE⋅AH，‎ ‎∵ tan∠DBG=‎‎1‎‎2‎，‎ ‎∴ 设HE＝x，则BE＝‎2x，‎ ‎∵ CH＝‎3‎，‎ ‎∴ AE＝CE＝‎3+x，‎ ‎∴ AH＝AE+HE＝‎3+2x，‎ ‎∴ AB‎2‎＝‎(3+x)⋅(3+2x)‎，‎ ‎∵ AB‎2‎＝BE‎2‎+AE‎2‎＝‎(2x‎)‎‎2‎+(3+x‎)‎‎2‎，‎ ‎∴ ‎(3+x)⋅(3+2x)‎＝‎(2x‎)‎‎2‎+(3+x‎)‎‎2‎，‎ 解得x＝‎1‎或‎0‎（舍去），‎ ‎∴ AB‎2‎＝‎(3+1)(3+2)‎＝‎20‎，‎ ‎∴ AB=2‎‎5‎，‎ 即‎⊙O的直径为‎2‎‎5‎．‎ ‎23.设y＝kx+b，‎ 将‎(25, 110)‎、‎(30, 100)‎代入，得：‎25k+b=110‎‎30k+b=100‎‎ ‎，‎ 解得：k=-2‎b=160‎‎ ‎，‎ ‎∴ y＝‎-2x+160‎；‎ 由题意得：‎(x-20)(-2x+160)‎＝‎1000‎，‎ 即‎-2x‎2‎+200x-3200‎＝‎1000‎，‎ 解得：x＝‎30‎或‎70‎，‎ 又∵ 每千克售价不低于成本，且不高于‎40‎元，即‎20≤x≤40‎，‎ 答：该超市要想获得‎1000‎的日销售利润，每千克樱桃的售价应定为‎30‎元．‎ 设超市日销售利润为w元，‎ w‎＝‎(x-20)(-2x+160)‎，‎ ‎＝‎-2x‎2‎+200x-3200‎，‎ ‎＝‎-2(x-50‎)‎‎2‎+1800‎，‎ ‎ 11 / 11‎ ‎∵ ‎-2<0‎，‎ ‎∴ 当‎20≤x≤40‎时，w随x的增大而增大，‎ ‎∴ 当x＝‎40‎时，w取得最大值为：w＝‎-2(40-50‎)‎‎2‎+1800‎＝‎1600‎，‎ 答：当每千克樱桃的售价定为‎40‎元时日销售利润最大，最大利润是‎1600‎元．‎ ‎24.证明：如图‎1‎中，‎ ‎∵ ‎∠AOB＝‎∠MON＝‎90‎‎∘‎，‎ ‎∴ ‎∠AOM＝‎∠BON，‎ ‎∵ AO＝BO，OM＝ON，‎ ‎∴ ‎△AOM≅△BON(SAS)‎．‎ ‎①证明：如图‎2‎中，连接AM．‎ 同法可证‎△AOM≅△BON，‎ ‎∴ AM＝BN，‎∠OAM＝‎∠B＝‎45‎‎∘‎，‎ ‎∵ ‎∠OAB＝‎∠B＝‎45‎‎∘‎，‎ ‎∴ ‎∠MAN＝‎∠OAM+∠OAB＝‎90‎‎∘‎，‎ ‎∴ MN‎2‎＝AN‎2‎+AM‎2‎，‎ ‎∵ ‎△MON是等腰直角三角形，‎ ‎∴ MN‎2‎＝‎2ON‎2‎，‎ ‎∴ NB‎2‎+AN‎2‎＝‎2ON‎2‎．‎ ‎②如图‎3-1‎中，设OA交BN于J，过点O作OH⊥MN于H．‎ ‎∵ ‎△AOM≅△BON，‎ ‎∴ AM＝BN，‎ ‎∴ ‎∠ANJ＝‎∠JOB＝‎90‎‎∘‎，‎ ‎∵ OM＝ON＝‎3‎，‎∠OMN＝‎90‎‎∘‎，OH⊥MN，‎ ‎∴ MN＝‎3‎‎2‎，MH＝HN=OH=‎‎3‎‎2‎‎2‎，‎ ‎∴ AH=OA‎2‎-OH‎2‎=‎4‎‎2‎‎-(‎‎3‎‎2‎‎2‎‎)‎‎2‎=‎‎46‎‎2‎，‎ ‎∴ BN＝AM＝MH+AH=‎‎46‎‎+3‎‎2‎‎2‎．‎ 如图‎3-2‎中，同法可证AM＝BN=‎‎46‎‎-3‎‎2‎‎2‎．‎ ‎25.∵ 抛物线y=-‎1‎‎3‎x‎2‎+bx+c交x轴于A(-3, 0)‎，B(4, 0)‎两点，‎ ‎ 11 / 11‎ ‎∴ y=-‎1‎‎3‎(x+3)(x-4)=-‎1‎‎3‎x‎2‎+‎1‎‎3‎x+4‎；‎ ‎①如图‎1‎，∵ B(4, 0)‎，C(0, 4)‎，‎ ‎∴ 设BC的解析式为：y＝kx+b，‎ 则‎4k+b=0‎b=4‎‎ ‎，解得k=-1‎b=4‎‎ ‎，‎ ‎∴ BC的解析式为：y＝‎-x+4‎，‎ ‎∴ ‎-x+4=‎3‎‎4‎x+‎‎9‎‎4‎，‎ 解得：x＝‎1‎，‎ ‎∴ E(1, 3)‎，‎ ‎∵ M(m, 0)‎，且MH⊥x轴，‎ ‎∴ G(m, ‎3‎‎4‎m+‎9‎‎4‎)‎，F(m, -‎1‎‎3‎m‎2‎+‎1‎‎3‎m+4)‎，‎ ‎∵ S‎△EFG‎=‎‎5‎‎9‎S‎△OEG，‎ ‎∴ ‎1‎‎2‎FG×(xE-xF)=‎5‎‎9‎×‎1‎‎2‎×OP(xE-xG)‎，‎ ‎[(-‎1‎‎3‎m‎2‎+‎1‎‎3‎m+4)-(‎3‎‎4‎m+‎9‎‎4‎)](1-m)=‎5‎‎9‎×‎9‎‎4‎(1-m)‎‎，‎ 解得：m‎1‎‎=‎‎3‎‎4‎，m‎2‎＝‎-2‎；‎ ‎②存在，由①知：E(1, 3)‎，‎ ‎∵ 四边形EFHP是正方形，‎ ‎∴ FH＝EF，‎∠EFH＝‎∠FHP＝‎∠HPE＝‎90‎‎∘‎，‎ ‎∵ M(m, 0)‎，且MH⊥x轴，‎ ‎∴ H(m, -m+4)‎，F(m, -‎1‎‎3‎m‎2‎+‎1‎‎3‎m+4)‎，‎ 分两种情况：‎ i)‎当‎-3≤m<1‎时，如图‎2‎，点F在EP的左侧，‎ ‎∴ FH＝‎(-m+4)-(-‎1‎‎3‎m‎2‎+‎1‎‎3‎m+4)=‎1‎‎3‎m‎2‎-‎4‎‎3‎m，‎ ‎∵ EF＝FH，‎ ‎∴ ‎1‎‎3‎m‎2‎‎-‎4‎‎3‎m=1-m，‎ 解得：m‎1‎‎=‎‎1+‎‎13‎‎2‎（舍），m‎2‎‎=‎‎1-‎‎13‎‎2‎，‎ ‎∴ H(‎1-‎‎13‎‎2‎, ‎7+‎‎13‎‎2‎)‎，‎ ‎∴ P(1, ‎7+‎‎13‎‎2‎)‎，‎ ii)‎当‎1