初中数学中考复习课件章节考点专题突破：第七章 图形变化 考点突破32 图形的相似 25页

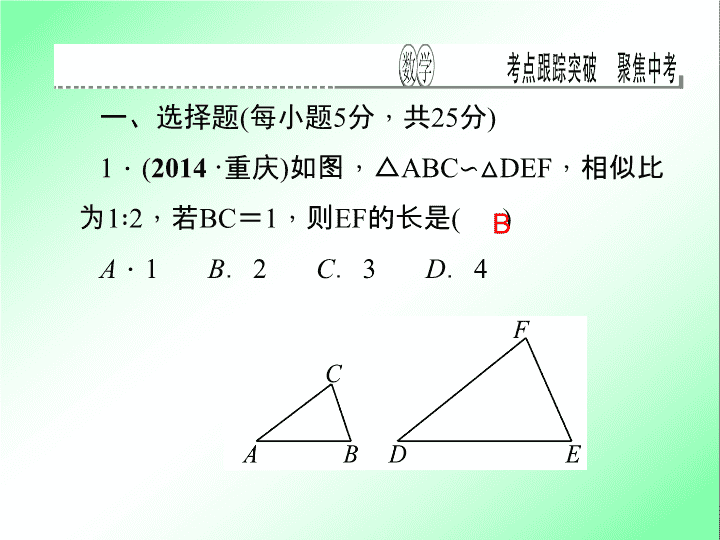
考点跟踪突破 32 　图形的相似 一、选择题 ( 每小题 5 分 ， 共 25 分 ) 1 ． ( 2014 · 重庆 ) 如图 ， △ ABC ∽△ DEF ， 相似比为 1 ∶ 2 ， 若 BC ＝ 1 ， 则 EF 的长是 ( ) A ． 1 B ． 2 C ． 3 D ． 4 B 2 ． ( 2014 · 泰安 ) 在 △ ABC 和 △ A 1 B 1 C 1 中 ， 下列四个命题： ① 若 AB ＝ A 1 B 1 ， AC ＝ A 1 C 1 ， ∠ A ＝ ∠ A 1 ， 则 △ ABC ≌△ A 1 B 1 C 1 ； ② 若 AB ＝ A 1 B 1 ， AC ＝ A 1 C 1 ， ∠ B ＝ ∠ B 1 ， 则 △ ABC ≌△ A 1 B 1 C 1 ； ③ 若 ∠ A ＝ ∠ A 1 ， ∠ C ＝ ∠ C 1 ， 则 △ ABC ∽△ A 1 B 1 C 1 ； ④ 若 AC ： A 1 C 1 ＝ CB ： C 1 B 1 ， ∠ C ＝ ∠ C 1 ， 则 △ ABC ∽△ A 1 B 1 C 1 . 其中真命题的个数为 ( ) A ． 4 B ． 3 C ． 2 D ． 1 B 3 ． ( 2014· 宁波 ) 如图 ， 梯形 ABCD 中 ， AD ∥ BC ， ∠ B ＝ ∠ ACD ＝ 90 ° ， AB ＝ 2 ， DC ＝ 3 ， 则 △ ABC 与 △ DCA 的 面积比为 ( ) A ． 2 ∶ 3 B ． 2 ∶ 5 C ． 4 ∶ 9 D . 2 ∶ 3 C 4 ． ( 2013· 孝感 ) 在平面直角坐标系中 ， 已知点 E ( － 4 ， 2 ) ， F ( － 2 ， － 2 ) ， 以原点 O 为位似中心 ， 相似比为 1 2 ， 把 △ EFO 缩小 ， 则点 E 的对应点 E? 的坐标是 ( ) A ． ( － 2 ， 1 ) B ． ( － 8 ， 4 ) C ． ( － 8 ， 4 ) 或 ( 8 ， － 4 ) D ． ( － 2 ， 1 ) 或 ( 2 ， － 1 ) D 5 ． ( 2014· 河北 ) 在研究相似问题时 ， 甲、乙两同学的观点如下： 甲：将边长为 3 ， 4 ， 5 的三角形按图中的方式向外扩张 ， 得到新 三角形 ， 它们的对应边间距均为 1 ， 则新三角形与原三角形相似． 乙：将邻边为 3 和 5 的矩形按图 ② 的方式向外扩张 ， 得到新的矩 形 ， 它们的对应边间距均为 1 ， 则新矩形与原矩形不相似． 对于两人的观点 ， 下列说法正确的是 ( ) A ． 两人都对 B ．两人都不对 C ． 甲对 ， 乙不对 D ．甲不对 ， 乙对 A 二、填空题 ( 每小题 5 分 ， 共 25 分 ) 6 ． ( 2014 · 邵阳 ) 如图 ， 在 ▱ ABCD 中 ， F 是 BC 上的一点 ， 直线 DF 与 AB 的延长线相交于点 E ， BP ∥ DF ， 且与 AD 相交于点 P ， 请从图中找出一组相似的三角形： __ ． △ ABP ∽△ AED( 答案不唯一 ) 7 ． ( 2014· 滨州 ) 如图 ， 平行于 BC 的直线 DE 把 △ ABC 分 成的两部分面积相等 ， 则 AD AB ＝ __ __ ． 8 ． ( 2013 · 安徽 ) 如图 ， P 为平行四边形 ABCD 边 AD 上一点 ， E ， F 分别为 PB ， PC 的中点 ， △ PEF ， △ PDC ， △ PAB 的面积分别为 S ， S 1 ， S 2 ， 若 S ＝ 2 ， 则 S 1 ＋ S 2 ＝ ____ ． 8 9 ． ( 2014 · 娄底 ) 如图 ， 小明用长为 3 m 的竹竿 CD 做测量工具 ， 测量学校旗杆 AB 的高度 ， 移动竹竿 ， 使竹竿与旗杆的距离 DB ＝ 12 m ， 则旗杆 AB 的高为 ____ m . 9 10 ． ( 2013 · 苏州 ) 如图 ， 在平面直角坐标系中 ， 四边形 OABC 是边长为 2 的正方形 ， 顶点 A ， C 分别在 x ， y 轴的正半轴上．点 Q 在对角线 OB 上 ， 且 QO ＝ OC ， 连接 CQ 并延长 CQ 交边 AB 于点 P. 则点 P 的坐标为 ． 三、解答题 ( 共 50 分 ) 11 ． (10 分 ) ( 2013 · 巴中 ) 如图 ， 在平行四边形 ABCD 中 ， 过点 A 作 AE ⊥ BC ， 垂足为点 E ， 连接 DE ， F 为线段 DE 上一点 ， 且 ∠ AFE ＝ ∠ B. (1) 求证： △ ADF ∽△ DEC ； (2) 若 AB ＝ 8 ， AD ＝ 6 3 ， AF ＝ 4 3 ， 求 AE 的长． 12 ． (10 分 ) ( 2014 · 巴中 ) 如图 ， 在平面直角坐标系 xOy 中 ， △ ABC 三个顶点坐标分别为 A( － 2 ， 4) ， B( － 2 ， 1) ， C( － 5 ， 2) ． (1) 请画出 △ ABC 关于 x 轴对称的 △ A 1 B 1 C 1 ； (2) 将 △ A 1 B 1 C 1 的三个顶点的横坐标与纵坐标同时乘以－ 2 ， 得到对应的点 A 2 ， B 2 ， C 2 ， 请画出 △ A 2 B 2 C 2 ； (3) 求 △ A 1 B 1 C 1 与 △ A 2 B 2 C 2 的面积比 ， 即 S △ A 1 B 1 C 1 ： S △ A 2 B 2 C 2 ＝ ____( 不写解答过 程 ， 直接写出结果 ) ． ∵ 将 △ A 1 B 1 C 1 的三个顶点的横坐标与纵坐标同时乘以－ 2 ， 得到对应的点 A 2 ， B 2 ， C 2 ， ∴△ A 1 B 1 C 1 与 △ A 2 B 2 C 2 的相似比为 1 ∶ 2 ， ∴ S △ A 1 B 1 C 1 ∶ S △ A 2 B 2 C 2 ＝ 1 ∶ 4 1∶4 13 ． (10 分 ) ( 2013 · 德宏州 ) 如图 ， 是一个照相机成像的示意图． (1) 如果像高 MN 是 35 mm ， 焦距是 50 mm ， 拍摄的景物高度 AB 是 4.9 m ， 拍摄点离景物有多远？ (2) 如果要完整的拍摄高度是 2 m 的景物 ， 拍摄点离景物有 4 m ， 像高不变 ， 则相机的焦距应调整为多少毫米？ 解：根据物体成像原理知： △ LMN ∽△ LBA ， ∴ MN AB ＝ LC LD .(1) ∵ 像高 MN 是 35 mm ， 焦距是 50 mm ， 拍摄的景物 高度 AB 是 4.9 m ， ∴ 35 50 ＝ 4.9 LD ， 解得 LD ＝ 7 ， ∴ 拍摄点距 离景物 7 米 (2) 拍摄高度是 2 m 的景物 ， 拍摄点离景物有 4 m ， 像高不 变 ， ∴ 35 LC ＝ 2 4 ， 解得 LC ＝ 70 ， ∴ 相机的焦距应调整为 70 mm 14 ． (10 分 ) ( 2014 · 遵义 ) 如图 ， ▱ ABCD 中 ， BD ⊥ AD ， ∠ A ＝ 45° ， E ， F 分别是 AB ， CD 上的 点 ， 且 BE ＝ DF ， 连接 EF 交 BD 于点 O. (1) 求证： BO ＝ DO ； 15 ． (10 分 ) ( 2013 · 衢州 ) (1) 提出问题 如图 ① ， 在等边 △ ABC 中 ， 点 M 是 BC 上的任意一点 ( 不含端点 B ， C) ， 连接 AM ， 以 AM 为边作等边 △ AMN ， 连接 CN. 求证： ∠ ABC ＝ ∠ ACN. (2) 若 EF ⊥ AB ， 延长 EF 交 AD 的延长线于点 G ， 当 FG ＝ 1 时 ， 求 AD 的长． (2) 类比探究 如图 ② ， 在等边 △ ABC 中 ， 点 M 是 BC 延长线上的任意一点 ( 不含端点 C) ， 其他条件不变 ， (1) 中结论 ∠ ABC ＝ ∠ ACN 还成立吗？请说明理由． (3) 拓展延伸 如图 ③ ， 在等腰 △ ABC 中 ， BA ＝ BC ， 点 M 是 BC 上的任意一点 ( 不含端点 B ， C) ， 连接 AM ， 以 AM 为边作等腰 △ AMN ， 使顶角 ∠ AMN ＝ ∠ ABC. 连接 CN. 试探究 ∠ ABC 与 ∠ ACN 的数量关系 ， 并说明理由．