中考数学第一轮复习导学案一次函数 8页

- 1 - 一次函数 ◆ 课前热身 1.一次函数 2yx的图象不．经过（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限 2．已知一次函数 21yx，则 y 随 x 的增大而_______________（填“增大”或“减小”）． 3．一次函数的图象过点（0，2），且函数 y 的值随自变量 x 的增大而增大，请写出一个符合 条件的函数解析式：_ ． 4．已知一次函数 y kx b的图象如图，当 0x  时， y 的取值范围是 ． 【参考答案】 1. D 2.增大 3.y＝kx＋2（k＞0 即可） 4. 2y  ◆考点聚焦 知识点 正比例函数及其图象、一次函数及其图象 大纲要求 1．理解正比例函数、一次函数的概念； 2．理解正比例函数、一次函数的性质； 3．掌握正比例函数和一次函数图象的画法；用待定系数法求正比例、一次函数的解析式； 考查重点与常见题型 1． 考查正比例函数、一次函数的定义、性质，有关试题常出现在选择题中 2． 综合考查正比例、一次函数的图像，习题的特点是在同一直角坐标系内考查两个函数的 图像，试题类型为选择题 3． 考查用待定系数法求正比例、一次函数的解析式，有关习题出现的频率很高，习题类型 有中档解答题和选拔性的综合题 y x O 1 -2 - 2 - ◆备考兵法 1.正比例函数与一次函数的关系 正比例函数是当 y=kx+b 中 b=0 时特殊的一次函数. 2.待定系数法确定正比例函数、一次函数的解析式 通常已知一点便可用待定系数法确定出正比例函数的解析式, 已知两点便可确定一次 函数解析式. 3.一次函数的图象 正比例函数 y=kx(k≠0)是过(0,0),(1,k)两点的一条直线;一次函数 y=kx+b(k≠0)是过 (0,b),( b k ,0)两点的一条直线. 4.直线 y=kx+b(k≠0)的位置与 k、b符号的关系 当 k>0 是直线 y=kx+b 过第一、三象限,当 k<0 时直线过第二、四象限;b 决定直线与 y 轴交 点的位置,b>0 直线交 y 轴于正半轴,b<0 直线交 y 轴于负半轴. 5.直线 L1 与 L2 的位置关系由 k、b 来确定 当直线 L1∥L2 时 k 相同 b 不同;当直线 L1 与 L2 重合时 k、b 都相同;当直线 L1 与 L2 相交于 y 轴同一点时,k 不同 b 相同. ◆考点链接 1．正比例函数的一般形式是__________．一次函数的一般形式是__________________. 2. 一次函数 y kx b的图象是经过 和 两点的 . 3. 求一次函数的解析式的方法是 ，其基本步骤是：⑴ ； ⑵ ； ⑶ ；⑷ . 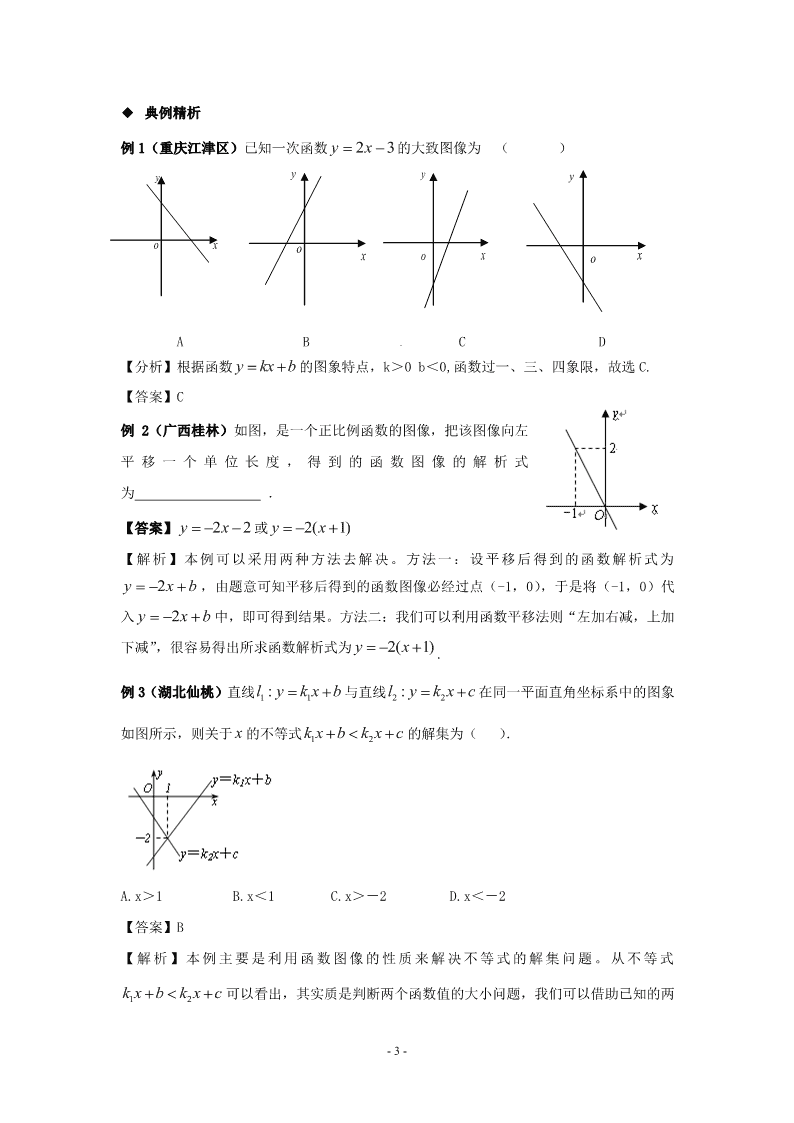4.一次函数 的图象与性质 k、b 的符号 k＞0b＞0 k＞0 b＜0 k＜0 b＞0 k＜0b＜0 图像的大 致位置 经过象限 第 象限 第 象限 第 象限 第 象限 性质 y 随 x 的增大 而 y 随 x 的增大 而 y 随 x 的增大 而 y 随 x 的增大 而 - 3 - ◆ 典例精析 例 1（重庆江津区）已知一次函数 32  xy 的大致图像为 （ ） A B C D 【分析】根据函数 y kx b的图象特点，k＞0 b＜0,函数过一、三、四象限，故选 C. 【答案】C 例 2（广西桂林）如图，是一个正比例函数的图像，把该图像向左 平 移 一 个 单 位 长 度 ， 得 到 的 函 数 图 像 的 解 析 式 为 ． 【答案】 22yx   或 2( 1)yx   【解 析】本例 可以采用两种 方法去解 决。方法一： 设平移后 得到的函数解 析式为 bxy  2 ，由题意可知平移后得到的函数图像必经过点（-1，0），于是将（-1，0）代 入 中，即可得到结果。方法二：我们可以利用函数平移法则“左加右减，上加 下减”，很容易得出所求函数解析式为 . 例 3（湖北仙桃）直线 11:l y k x b与直线 22:l y k x c在同一平面直角坐标系中的图象 如图所示，则关于 x 的不等式 12k x b k x c   的解集为（ ）． A.x＞1 B.x＜1 C.x＞－2 D.x＜－2 【答案】B 【 解 析 】 本 例 主 要 是 利 用 函 数 图 像 的 性 质 来 解 决 不 等 式 的 解 集 问 题 。 从 不 等 式 可以看出，其实质是判断两个函数值的大小问题，我们可以借助已知的两 o y x o oo - 4 - 个函数图像进行判别。由图可知两个函数有一个交点（1，-2），因此，从交点的左右两边很 容易判断两个函数值的大小。 例 3（江苏省）某加油站五月份营销一种油品的销售利润 y （万元）与销售量 x （万升）之 间函数关系的图象如图中折线所示，该加油站截止到 13 日调价时的销售利润为 4 万元，截 止至 15 日进油时的销售利润为 5.5 万元．（销售利润＝（售价－成本价）×销售量） 请你根据图象及加油站五月份该油品的所有销售记录提供的信息，解答下列问题： （1）求销售量 x 为多少时，销售利润为 4 万元； （2）分别求出线段 AB 与 BC 所对应的函数关系式； （3）我们把销售每升油所获得的利润称为利润率，那么，在 OA.AB.BC 三段所表示的销售 信息中，哪一段的利润率最大？（直接写出答案） 【答案】（1）根据题意，当销售利润为 4 万元，销售量为 4 (5 4) 4   （万升）． 答：销售量 x 为 4 万升时销售利润为 4 万元． （2）点 A 的坐标为(4 4)， ，从 13 日到 15 日利润为5.5 4 1.5 （万元）， 所以销售量为1.5 (5.5 4) 1   （万升），所以点 B 的坐标为(5 5.5)， ． 设线段 AB 所对应的函数关系式为 y kx b，则 44 5.5 5 . kb kb    ， 解得 1.5 2. k b    ， 线段 所对应的函数关系式为 1.5 2(4 5)y x x≤ ≤ ． 从 15 日到 31 日销售 5 万升，利润为1 1.5 4 (5.5 4.5) 5.5     （万元）． 本月销售该油品的利润为5.5 5.5 11（万元），所以点C 的坐标为(1011)， ． 设线段 BC 所对应的函数关系式为 y mx n，则 5.5 5 11 10 . mn mn    ， 解得 1.1 0. m n    ， 所以线段 BC 所对应的函数关系式为 1.1 (5 10)yxx ≤ ≤ ． - 5 - （3）线段 AB ． 【解析】本题从油品销售的现实情境中构造试题，题目呈现形式直观明确，梯度明显。图象 是常见的销售与利润的位移图，问题背景为学生所熟悉，涉及点的坐标、函数等知识领域以 及数形结合等数学思想方法，具有一定的综合性。解决问题的关键在于正确读取图表中的信 息，即把相关信息转化为图象上点的 坐标、一次函数关系式等，对读图、获取信息能力有 较高要求。主要考查与函数图象相关的数学问题的分析、探究与解决能力，增强其应用意识。 有较好的信度和区分度。 ◆ 迎考精炼 一、选择题 1．(陕西省)若正比例函数的图像经过点（－1，2），则这个图像必经过点（ ） A．(1，2) B．(－1，－2) C．(2，－1) D．(1，－2) 2.（湖南株洲）一次函数 2yx的图象不．经过（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限 3. （ 安 徽 ） 已知函数 y kx b的 图 象 如 图 ， 则 2y kx b的图象可能是（ ） 4．（湖北宜昌）由于干旱，某水库的蓄水量随时间的增加而直线下降．若该水库的蓄水量 V(万米 3)与干旱的时间 t(天)的关系如图所示，则下列说法正确的是( )． /天t /万米3V 200 400 600 800 1000 1200 O 5040302010 A．干旱开始后，蓄水量每天减少 20 万米 3 B．干旱开始后，蓄水量每天增加 20 万米 3 C．干旱开始时，蓄水量为 200 万米 3 D．干旱第 50 天时，蓄水量为 1 200 万米 3 - 6 - 5．（浙江舟山）P1(x1，y1)，P2(x2，y2)是正比例函数 y= -x 图象上的两点，则下列判断正确 的是（ ） A．y1>y2 B．y1y2 D．当 x1