初中数学中考复习课件章节考点专题突破：第五章 图形性质1-20 三角形与全等三角形 16页

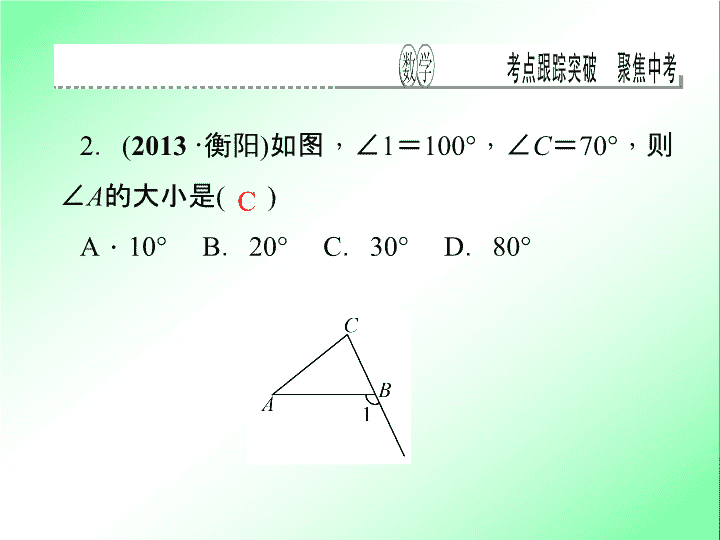
考点跟踪突破 20 　三角形与全等三角形 一、选择题 ( 每小题 6 分 ， 共 30 分 ) 1 ． ( 2014 · 邵阳 ) 如图 ， 在 △ ABC 中 ， ∠ B ＝ 46° ， ∠ C ＝ 54° ， AD 平分 ∠ BAC ， 交 BC 于点 D ， DE ∥ AB ， 交 AC 于点 E ， 则 ∠ ADE 的大小是 ( ) A ． 45° B ． 54° C ． 40° D ． 50° C 2 ． ( 2013 · 衡阳 ) 如图 ， ∠ 1 ＝ 100° ， ∠ C ＝ 70° ， 则 ∠ A 的大小是 ( ) A ． 10° B ． 20° C ． 30° D ． 80° C 3 ． ( 2012 · 南通 ) 如图 ， 在 △ ABC 中 ， ∠ C ＝ 70° ， 沿图中虚线截去 ∠ C ， 则 ∠ 1 ＋ ∠ 2 ＝ ( ) A ． 360° B ． 250° C ． 180° D ． 140° B 4 ． ( 2014 · 威海 ) 如图 ， 在 △ ABC 中 ， ∠ ABC ＝ 50° ， ∠ ACB ＝ 60° ， 点 E 在 BC 的延长线上 ， ∠ ABC 的平分线 BD 与 ∠ ACE 的平分线 CD 相交于点 D ， 连接 AD ， 下列结论中不正确的是 ( ) A ． ∠ BAC ＝ 70° B ． ∠ DOC ＝ 90° C ． ∠ BDC ＝ 35° D ． ∠ DAC ＝ 55° B 5 ． ( 2013 · 铁岭 ) 如图，在 △ ABC 和 △ DEC 中 ， 已知 AB ＝ DE ， 还需添加两个条件才能使 △ ABC ≌△ DEC ， 不能添加的一组条件是 ( ) A ． BC ＝ EC ， ∠ B ＝ ∠ E B ． BC ＝ EC ， AC ＝ DC C ． BC ＝ DC ， ∠ A ＝ ∠ D D ． ∠ B ＝∠ E ， ∠ A ＝∠ D C 二、填空题 ( 每小题 6 分 ， 共 30 分 ) 6 ． ( 2014 · 广州 ) 在 △ ABC 中 ， 已知 ∠ A ＝ 60° ， ∠ B ＝ 80° ， 则 ∠ C 的外角的度数是 ． 7 ． ( 2014 · 长沙 ) 如图 ， 点 B ， E ， C ， F 在一条直线上 ， AB ∥ DE ， AB ＝ DE ， BE ＝ CF ， AC ＝ 6 ， 则 DF ＝ ____ ． 140° 6 8 ． ( 2013 · 白银 ) 如图 ， 已知 BC ＝ EC ， ∠ BCE ＝ ∠ ACD ， 要使 △ ABC ≌△ DEC ， 则应添加的一个条件为 ． ( 答案不唯一 ， 只需填一个 ) AC ＝ DC( 答案不唯一 ) 9 ． ( 2012 · 乐山 ) 如图 ， ∠ ACD 是 △ ABC 的外角 ， ∠ ABC 的平分线与 ∠ ACD 的平分线交于点 A 1 ， ∠ A 1 BC 的平分线与 ∠ A 1 CD 的平分线交于点 A 2 ， … ， ∠ A n － 1 BC 的平分线与 ∠ A n － 1 CD 的平分线交于点 A n ， 设 ∠ A ＝ θ. 则： (1) ∠ A 1 ＝ ____ ； (2) ∠ A n ＝ ____ ． 10 ． ( 2012 · 黄石 ) 将下列正确命题的序号填在横线上 ____ ． ① 若 n 为大于 2 的正整数 ， 则 n 边形的所有外角之和为 (n － 1) · 180° ； ② 三角形的三条中线的交点就是三角形的重心； ③证明两个三角形全等的方法有： SSS ， SAS ， ASA ， SSA 及 HL 等． ② 三、解答题 ( 共 40 分 ) 11 ． (10 分 ) ( 2014 · 武汉 ) 如图 ， AC 和 BD 相交于点 O ， OA ＝ OC ， OB ＝ OD. 求证： DC ∥ AB. 12 ． (10 分 ) ( 2014 · 宜宾 ) 如图 ， 在 △ AFD 和 △ CEB 中 ， 点 A ， E ， F ， C 在同一直线上 ， AE ＝ CF ， ∠ B ＝ ∠ D ， AD ∥ BC. 求证： AD ＝ BC. 13 ． (10 分 ) ( 2013 · 佛山 ) 课本指出：公认的真命题称为公理 ， 除了公理外 ， 其他的真命题 ( 如推论、定理等 ) 的正确性都需要通过推理的方法证实． (1) 叙述三角形全等的判定方法中的推论 AAS ； (2) 证明推论 AAS . 要求：叙述推论用文字表达；用图形中的符号表达已知、求证 ， 并证明 ， 证明对各步骤要注明依据． 解： (1) 三角形全等的判定方法中的推论 AAS 指的是：两角及其中一 角的对边对应相等的两个三角形全等 (2) 已知：在 △ ABC 与 △ DEF 中 ， ∠ A ＝ ∠ D ， ∠ C ＝ ∠ F ， B C ＝ EF. 求证： △ ABC ≌△ DEF. 证明：如图 ， 在 △ ABC 与 △ DEF 中 ， ∠ A ＝ ∠ D ， ∠ C ＝ ∠ F( 已知 ) ， ∴∠ A ＋ ∠ C ＝ ∠ D ＋ ∠ F ( 等量代换 ) ．又 ∵∠ A ＋ ∠ B ＋ ∠ C ＝ 180 ° ， ∠ D ＋ ∠ E ＋ ∠ F ＝ 180 ° ( 三角形内角和 定理 ) ， ∴∠ B ＝ ∠ E ， ∴ 在 △ ABC 与 △ DEF 中 ， î ï í ï ì ∠ C ＝ ∠ F ， BC ＝ EF ， ∠ B ＝ ∠ E ， ∴△ ABC ≌△ DEF ( ASA ) 14 ． (10 分 ) ( 2014 · 杭州 ) 在 △ ABC 中 ， AB ＝ AC ， 点 E ， F 分别在 AB ， AC 上 ， AE ＝ AF ， BF 与 CE 相交于点 P. 求证： PB ＝ PC ， 并直接写出图中其他相等的线段． 解：在 △ ABF 和 △ ACE 中 ， î ï í ï ì AB ＝ AC ， ∠ BAF ＝ ∠ CAE ， AF ＝ AE ， ∴△ ABF ≌△ ACE ( SAS ) ， ∴∠ ABF ＝ ∠ ACE( 全等三角形的对应角相等 ) ， ∴ BF ＝ CE( 全等三角形的对应边相等 ) ， ∵ AB ＝ AC ， AE ＝ AF ， ∴ BE ＝ CF ， 在 △ BEP 和 △ CFP 中 ， î ï í ï ì ∠ BPE ＝ ∠ CPF ， ∠ PBE ＝ ∠ PCF ， BE ＝ CF ， ∴△ BEP ≌△ CFP ( AAS ) ， ∴ PB ＝ PC ， ∵ BF ＝ CE ， ∴ PE ＝ PF ， ∴ 图中相等的线段为 PE ＝ PF ， BE ＝ CF