江西专版2020中考数学复习方案第四单元图形的初步认识与三角形第15课时平面图形与相交线平行线课件 27页

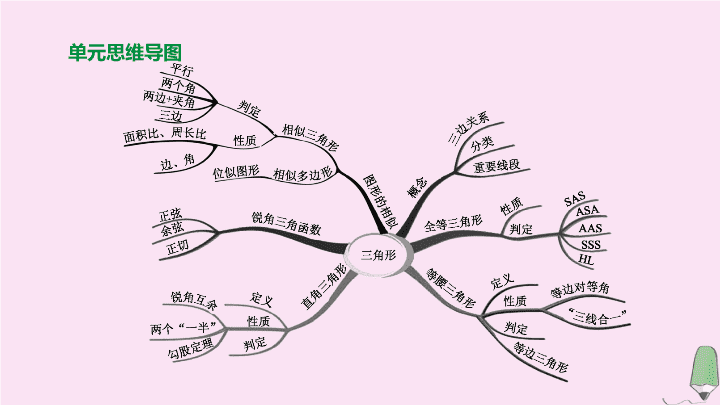
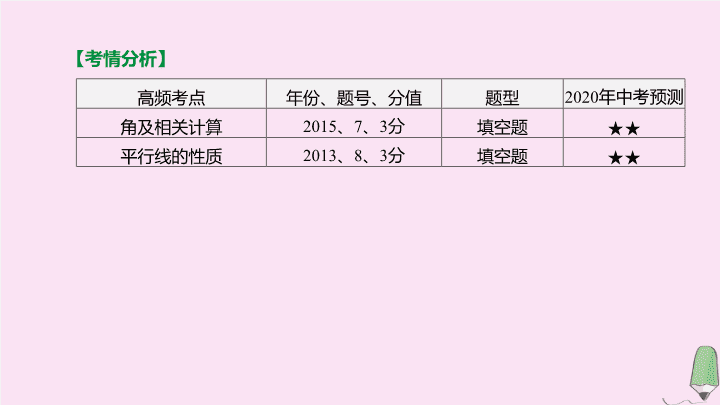
单元思维导图 第 15 课时 平面图形与相交线、平行线 第四单元 图形的初步认识与三角形 【 考情分析 】 高频考点 年份、题号、分值 题型 2020 年中考预测 角及相关计算 2015 、 7 、 3 分 填空题 ★★ 平行线的性质 2013 、 8 、 3 分 填空题 ★★ 考点一　直线、射线、线段 考点聚焦 1 . 直线的性质 (1) 两直线相交 , 只有 ① 　　　　 个交点 ;(2) 经过两点有且只有一条直线 , 即两点确定 ② 　　　　 条直线 .  2 . 线段的基本事实 两点之间 , ③ 　　　　 最短 .  3 . 线段的中点 如果点 B 把线段 AC 分成相等的两条线段 AB 和 BC , 那么点 B 叫做线段 AC 的 ④ 　　　　 , 即 AB=BC= ⑤ 　　　　 AC.  一 一 线段 中点 考点二　角 ∠BOC ∠AOB 2 2 2 . 余角和补角 (1) 定义 : 若 α + β= ⑩ 　　　　 , 则 α , β 互为余角 .  若 α + β= ⑪ 　　　　 , 则 α , β 互为补角 .  (2) 性质 : 同角 ( 或等角 ) 的余角 ⑫ 　　　　 ; 同角 ( 或等角 ) 的补角 ⑬ 　　　　 .  3 . 角度之间的转换关系 : 1° = ⑭ 　　　　 ' ,1 '= 60 ″ ,1° = ⑮ 　　　　　 ″.  90° 180° 相等 相等 60 3600 考点三　相交线 1 . 在同一平面内 , 两条直线只有两种位置关系 : ⑯ 　　　　 , ⑰ 　　　　 .  2 . 垂线的性质 : (1) 在同一平面内 , 经过一点有 ⑱ 　　 　　 条直线垂直于已知直线 ; (2) 直线外一点与直线上各点连接的所有线段中 , ⑲ 　　　　 最短 .  3 . 点到直线的距离 : 从直线外一点向已知直线作垂线 , 这一点和垂足之间线段的长度叫做点到这条直线的距离 . 4 . 对顶角的性质 : 对顶角 ⑳ 　　　　 .  相交 平行 且只有一 垂线段 相等 考点四　平行线 1 . 三线八角 名称 关键点回顾 图形 　 直线 a , b 被直线 l 所截 , 构成八个角 ( 如图 ) 同位角 　 ∠ 1 和 ∠ 5, ∠ 4 和 ∠ 8, ∠ 2 和 ∠ 6, ∠ 3 和 ∠ 7 是同位角 内错角 ∠ 2 和 ∠ 8, ∠ 3 和 ∠ 5 是内错角 同 旁内角 ∠ 2 和 ∠ 5, ∠ 3 和 ∠ 8 是同旁内角 题组一　必会题 对点演练 1 . [2019· 长沙 ] 如图 15-1, 平行线 AB , CD 被直线 AE 所截 , ∠ 1 = 80°, 则∠ 2 的度数是 ( 　　 ) A . 80° B . 90° C . 100° D . 110° 图 15-1 [ 答案 ] C 　 [ 解析 ] ∵∠ 1 = 80°, ∴∠ 3 = 100° . ∵ AB ∥ CD , ∴∠ 2 = ∠ 3 = 100° . 故选 C . 2 . [2019· 河南 ] 如图 15-2, AB ∥ CD , ∠ B= 75°, ∠ E= 27°, 则∠ D 的度数为 ( 　　 ) A . 45° B . 48° C . 50° D . 58° 图 15-2 B 3 . [2019· 怀化 ] 与 30° 的角互为余角的角的度数是 ( 　　 ) A . 30° B . 60° C . 70° D . 90° B 4 . [2019· 天门 ] 如图 15-3, CD ∥ AB , 点 O 在 AB 上 , OE 平分∠ BOD , OF ⊥ OE , ∠ D= 110°, 则∠ AOF 的度数是 ( 　　 ) A . 20° B . 25° C . 30° D . 35° 图 15-3 [ 答案 ] D 　 [ 解析 ] ∵ CD ∥ AB , ∴∠ DOB= ∠ D= 110°, ∴∠ AOD= 70° . ∵ OE 平分∠ BOD , ∴∠ DOE= 55° . ∵ OF ⊥ OE , ∴∠ FOE= 90°, ∴∠ DOF= 90°-55° = 35°, ∴∠ AOF= 70°-35° = 35° . 故选 D . 5 . 如图 15-4, C , D 是线段 AB 上两点 . 若 CB= 4 cm, DB= 7 cm, 且点 D 是线段 AC 的中点 , 则 AB= 　　　　 cm .  图 15-4 10 题组二　易错题 【 失分点 】 忽视分类讨论或分类讨论不全 ; 余角和补角的概念易混淆 ; 对 “ 三线八角 ” 理解有误 ; 混淆平行线的性质定理 . 6 . [2019· 邵阳 ] 如图 15-5, 已知两直线 l 1 与 l 2 被第三条直线 l 3 所截 , 下列等式一定成立的是 ( 　　 ) A . ∠ 1 = ∠ 2 B . ∠ 2 = ∠ 3 C . ∠ 2+ ∠ 4 = 180° D . ∠ 1+ ∠ 4 = 180° 图 15-5 [ 答案 ] D 　 [ 解析 ] ∠ 1 与∠ 2 是同位角 , ∠ 2 与∠ 3 是内错角 , ∠ 2 与∠ 4 是同旁内角 , 由平行线的性质可知 , 选项 A,B,C 成立的条件为 l 1 ∥ l 2 时 , 而∠ 1 与∠ 4 是邻补角 , 故选项 D 正确 . 7 . [2019· 广州 ] 一副三角板如图 15-6 放置 , 将三角板 ADE 绕点 A 逆时针旋转 α (0° <α < 90°), 使得三角板 ADE 的一边所在的直线与 BC 垂直 , 则 α 的度数为 　　　　 .  图 15-6 [ 答案 ] 15° 或 60° 　 [ 解析 ] 分情况讨论 : ①当 DE ⊥ BC 时 , ∠ BAD= 180°-60°-45° = 75°, ∴ α= 90°- ∠ BAD= 15°; ②当 AD ⊥ BC 时 , α= 90°- ∠ C= 90°-30° = 60° . 故答案为 :15° 或 60° . 8 . 如果一个角等于它的余角的 2 倍 , 那么这个角的补角是 　　　　 度 .  120 考向一　线段、角的有关计算 例 1 [2019· 福建 ] 如图 15-7, 数轴上 A , B 两点所表示的数分别是 -4 和 2, C 是线段 AB 的中点 , 则点 C 所表示的数是 　　　　 .  -1 图 15-7 例 2 (1) [2019· 岳阳 ] 如图 15-8, 已知 BE 平分∠ ABC , 且 BE ∥ DC , 若∠ ABC= 50°, 则∠ C 的度数是 ( 　　 ) A . 20° B . 25° C . 30° D . 50° 图 15-8 (2) [2019· 湖州 ] 已知∠ α= 60°32 ' , 则∠ α 的余角是 ( 　　 ) A . 29°28 ' B . 29°68 ' C . 119°28 ' D . 119°68 ' B A 【 方法点析 】 在以线、角、三角板等图形为背景的题中 , 应着眼于一些比较特殊的平角、角平分线、互余、互补、垂直等概念 , 立足于基本性质 , 构建相关量之间的位置及数量关系进行分析与解题 . | 考向精练 | 1 . 如图 15-9, 直线 AC 和直线 BD 相交于点 O , OE 平分∠ BOC. 若∠ 1+ ∠ 2 = 80°, 则∠ 3 的度数为 ( 　　 ) A . 40° B . 50° C . 60° D . 70° 图 15-9 D 2 . [2015· 江西 7 题 ] 一个角的度数为 20°, 则它的补角的度数为 　　　　 .  160° 考向二　平行线的性质及判定 例 3 (1) 如图 15-10, 直线 a ∥ b , ∠ 1 = 50°, ∠ 2 = 40°, 则∠ 3 的度数为 ( 　　 ) A . 40° B . 90° C . 50° D . 100° 图 15-10 B 例 3 (2) [2019· 济宁 ] 如图 15-11, 直线 a , b 被直线 c , d 所截 , 若∠ 1 = ∠ 2, ∠ 3 = 125°, 则∠ 4 的度数是 ( 　　 ) A . 65° B . 60° C . 55° D . 75° 图 15-11 C | 考向精练 | 1 . [2013· 江西 8 题 ] 如图 15-12, 在 △ ABC 中 , ∠ A = 90°, 点 D 在 AC 边上 , DE ∥ BC , 若∠ 1 = 155°, 则∠ B 的度数为 　　　　 .  图 15-12 [ 答案 ] 65° 　 [ 解析 ] ∵∠ 1 = 155°, ∠ 1 是∠ EDC 的补角 , ∴∠ EDC= 180°- ∠ 1 = 25° . ∵ DE ∥ BC , ∴∠ C= ∠ EDC= 25° . 又在 Rt△ ABC 中 , ∠ A= 90°, ∴∠ B= 90°- ∠ C= 65° . 2 . [2019· 山西 ] 如图 15-13, 在 △ ABC 中 , AB=AC , ∠ A= 30°, 直线 a ∥ b , 顶点 C 在直线 b 上 , 直线 a 交 AB 于点 D , 交 AC 于点 E , 若∠ 1 = 145°, 则∠ 2 的度数是 ( 　　 ) A . 30° B . 35° C . 40° D . 45° [ 答案 ] C 　 [ 解析 ] 在 △ ABC 中 , AB=AC , ∠ A= 30°, ∴∠ ABC= 75° . ∵∠ 1 = 145°, ∴∠ FDB= 35° . 过点 B 作 BG ∥ a , 如图 . ∵ a ∥ b , ∴ BG ∥ b , ∴∠ FDB= ∠ DBG , ∠ 2 = ∠ CBG. ∵∠ ABC= ∠ ABG + ∠ CBG , ∴∠ 2 = 75°-35° = 40° . 故选 C . 图 15-13 3 . [2019· 东营 ] 将一副三角板 ( ∠ A= 30°, ∠ E= 45°) 按如图 15-14 所示方式摆放 , 使得 BA ∥ EF , 则∠ AOF 等于 ( 　　 ) A . 75° B . 90° C . 105° D . 115° 图 15-14 [ 答案 ] A 　 [ 解析 ] ∵ BA ∥ EF , ∠ A= 30°, ∴∠ FCA= ∠ A= 30° . ∵∠ F= ∠ E= 45°, ∴∠ AOF= ∠ FCA + ∠ F= 30°+45° = 75° . 故选 A . 4 . [2016· 江西 13(2) 题 ] 如图 15-15, 在 Rt△ ABC 中 , ∠ ACB= 90°, 将 Rt△ ABC 向下翻折 , 使点 A 与点 C 重合 , 折痕为 DE , 求证 : DE ∥ BC. 图 15-15 证明 : 由题易知 AD=CD. 又∵点 A 与点 C 重合 , ∴ EA=EC , DE ⊥ AC. ∵∠ ACB= 90°, ∴ AC ⊥ BC , ∴ DE ∥ BC.