2009中考数学分类汇编-概率 6页

‎30．概率 一、选择题 ‎1、（2009呼和浩特）有一个正方体，6个面上分别标有1~6这6个整数，投掷这个正方体一次，则出现向上一面的数字是偶数的概率为（ ）‎ A． B． C． D．‎ ‎【关键词】列举法，树形图 ‎【答案】‎ ‎2、（2009青海）将三个均匀的六面分别标有1、2、3、4、5、6的正方体同时掷出，出现的数字分别为，则正好是直角三角形三边长的概率是（ ）‎ A． B． C． D．‎ 概率的应用 ‎【关键词】‎ ‎【答案】D ‎3、（2009年黄石市）为了防控输入性甲型H1N1流感，某市医院成立隔离治疗发热流涕病人防控小组，决定从内科5位骨干医师中（含有甲）抽调3人组成，则甲一定抽调到防控小组的概率是（ ）‎ A． B． C． D．‎ ‎【关键词】频率估计概率；概率的应用 ‎【答案】A 一、 填空题 ‎1、（2009年枣庄市）13．布袋中装有1个红球，2个白球，3个黑球，它们除颜色外完全相同，从袋中任意摸出一个球，摸出的球是白球的概率是 ．‎ ‎【关键词】概率 ‎【答案】‎ ‎2、（2009年佳木斯）甲、乙两人玩抽扑克牌游戏，游戏规则是：从牌面数字分别为5、6、7的三张扑克牌中。随机抽取一张，放回后，再随机抽取一张，若所抽的两张牌面数字的积为奇数，则甲获胜；若所抽取的两张牌面数字的积为偶数，则乙获胜，这个游戏 （填“公平”或“不公平”）‎ ‎3、（2009年赤峰市）如右图，是由四个直角边分别是3和4的全等的直角三角形拼成的“赵爽弦图”，小亮随机的往大正方形区域内投针一次，则针扎在阴影部分的概率是 ‎ ‎4、（2009青海）在一个不透明的布袋中，红色、黑色、白色的玻璃球共有60个，除颜色外，形状、大小、质地等完全相同．小刚通过多次摸球实验后发现其中摸到红色、黑色球的频率稳定在15%和45%，则口袋中白色球的个数很可能是 个．‎ ‎【关键词】概率综合题 ‎【答案】24‎ ‎5、（2009年龙岩）在3 □ 2 □（－2）的两个空格□中，任意填上“+”或“－”，则运算结果为3的概率是 ．‎ ‎【关键词】概率的应用 ‎【答案】 ．‎ ‎6、（2009年广东省）在一个不透明的布袋中装有2个白球和个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球，摸到黄球的概率是，则__________．‎ ‎【关键词】概率的应用；解分式方程 ‎【答案】8‎ ‎7、（2009年邵阳市）晓芳抛一枚硬币10次，有7次正面朝上，当她抛第11次时，正面向上的概率为______。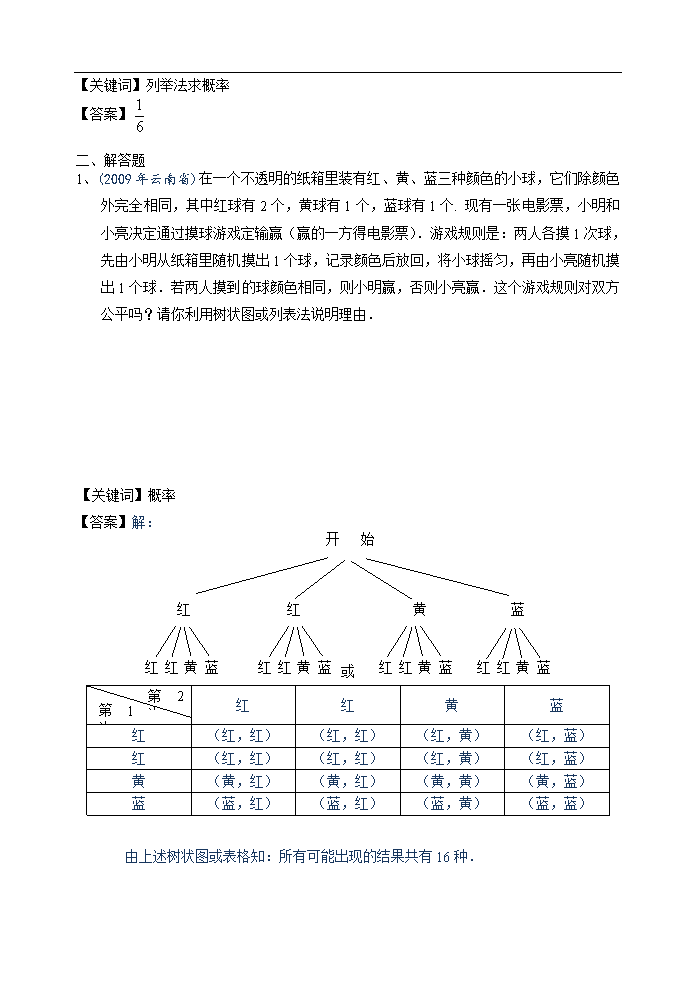‎ ‎【关键词】频率估计概率；概率的应用 ‎【答案】‎ ‎8、（2009年黄石市）汶川大地震时，航空兵空投救灾物质到指定的区域（圆A）如图所示，若要使空投物质落在中心区域（圆B）的概率为，则与的半径之比为 ．‎ A B ‎【关键词】频率估计概率；概率的应用 ‎【答案】‎ ‎9、（2009年铁岭市）如图所示，小区公园里有一块圆形地面被黑白石子铺成了面积相等的八部分，阴影部分是黑色石子，小华随意向其内部抛一个小球，则小球落在黑色石子区域内的概率是 ．‎ ‎【关键词】频率估计概率；概率的应用 ‎【答案】‎ ‎10、（2009绵阳）一天晚上，小伟帮妈妈清洗茶杯，三个茶杯只有花色不同，其中一个无盖（如图），突然停电了，小伟只好把杯盖与茶杯随机地搭配在一起，则花色完全搭配正确的概率是 ．‎ ‎【关键词】列举法求概率 ‎【答案】‎ 一、 解答题 ‎1、(2009年云南省)在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球，它们除颜色外完全相同，其中红球有2个，黄球有1个，蓝球有1个. 现有一张电影票，小明和小亮决定通过摸球游戏定输赢（赢的一方得电影票）．游戏规则是：两人各摸1次球，先由小明从纸箱里随机摸出1个球，记录颜色后放回，将小球摇匀，再由小亮随机摸出1个球．若两人摸到的球颜色相同，则小明赢，否则小亮赢．这个游戏规则对双方公平吗？请你利用树状图或列表法说明理由．‎ ‎【关键词】概率 ‎【答案】开 始 红 　　　 红 　　　　　 黄 　蓝 红 红 黄 蓝 红 红 黄 蓝 红 红 黄 蓝 红 红 黄 蓝 解：‎ ‎ ‎ ‎ ‎ ‎　‎ 或 第2次 第1次 红 红 黄 蓝 红 ‎（红，红）‎ ‎（红，红）‎ ‎（红，黄）‎ ‎（红，蓝）‎ 红 ‎（红，红）‎ ‎（红，红）‎ ‎（红，黄）‎ ‎（红，蓝）‎ 黄 ‎（黄，红）‎ ‎（黄，红）‎ ‎（黄，黄）‎ ‎（黄，蓝）‎ 蓝 ‎（蓝，红）‎ ‎（蓝，红）‎ ‎（蓝，黄）‎ ‎（蓝，蓝）‎ ‎ ‎ 由上述树状图或表格知：所有可能出现的结果共有16种．‎ P（小明赢）=，P（小亮赢）=．‎ ‎∴此游戏对双方不公平，小亮赢的可能性大．‎ ‎（说明：答题时只需用树状图或列表法进行分析即可）‎ ‎2、（2009年崇左）一只口袋中放着若干只红球和白球，这两种球除了颜色以外没有任何其他区别，袋中的球已经搅匀，蒙上眼睛从口袋中取出一只球，取出红球的概率是．‎ ‎（1）取出白球的概率是多少？‎ ‎（2）如果袋中的白球有18只，那么袋中的红球有多少只？‎ ‎【关键词】利用概率的计算公式进行计算。‎ ‎【答案】‎ ‎（1）‎ ‎=‎ ‎（2）设袋中的红球有只，则有 ‎ （或）‎ 解得 所以，袋中的红球有6只．‎ ‎3、（2009贺州）一个不透明的布袋里装有4个大小、质地均相同的乒乓球，‎ 每个球上面分别标有1，2，3，4．小林先从布袋中随机抽取一个乒乓球（不放回去），再从剩下的3个球中随机抽取第二个乒乓球．‎ ‎（1）请你列出所有可能的结果；‎ ‎（2）求两次取得乒乓球的数字之积为奇数的概率．‎ ‎【关键词】列表计算概率 ‎【答案】解：（1）根据题意列表如下：‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎1‎ ‎（1，2）‎ ‎（1，3）‎ ‎（1，4）‎ ‎2‎ ‎（2，1）‎ ‎（2，3）‎ ‎（2，4）‎ ‎3‎ ‎（3，1）‎ ‎（3，2）‎ ‎（3，4）‎ ‎4‎ ‎（4，1）‎ ‎（4，2）‎ ‎（4，3）‎ 由以上表格可知：有12种可能结果 ‎ ‎（注：用其它方法得出正确的结果，也给予相应的分值）‎ ‎（2）在（1）中的12种可能结果中，两个数字之积为奇数的只有2种，‎ 所以，P（两个数字之积是奇数）．‎ ‎4、（2009年山西省）某商场为了吸引顾客，设计了一种促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“10元”、“20元”和“30元”的字样．规定：顾客在本商场同一日内，每消费满200元，就可以在箱子里先后摸出两个球（第一次摸出后不放回）．商场根据两小球所标金额的和返还相应价格的购物券，可以重新在本商场消费．某顾客刚好消费200元．‎ ‎（1）该顾客至少可得到 元购物券，至多可得到 元购物券；‎ ‎（2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于30元的概率．‎ ‎【关键词】概率的应用；列举法，树形图 ‎【答案】解：（1）10，50；‎ ‎ （2）解：解法一（树状图）：‎ ‎0‎ ‎10‎ ‎20‎ ‎30‎ ‎10‎ ‎20‎ ‎30‎ ‎10‎ ‎0‎ ‎20‎ ‎30‎ ‎10‎ ‎30‎ ‎40‎ ‎0‎ ‎10‎ ‎30‎ ‎20‎ ‎20‎ ‎30‎ ‎50‎ ‎20‎ ‎30‎ ‎0‎ ‎10‎ ‎50‎ ‎30‎ ‎40‎ 第一次 第二次 和 ‎ （6分）‎ 从上图可以看出，共有12种可能结果，其中大于或等于30元共有8种可能结果，因此（不低于30元）=‎ 解法二（列表法）：‎ 第一次 第二次 ‎0‎ ‎10‎ ‎20‎ ‎30‎ ‎0‎ ‎10‎ ‎20‎ ‎30‎ ‎10‎ ‎10‎ ‎30‎ ‎40‎ ‎20‎ ‎20‎ ‎30‎ ‎50‎ ‎30‎ ‎30‎ ‎40‎ ‎50‎ ‎（以下过程同“解法一”）‎ ‎5、（2009年铁岭市）小明和小亮是一对双胞胎，他们的爸爸买了两套不同品牌的运动服送给他们，小明和小亮都想先挑选．于是小明设计了如下游戏来决定谁先挑选．游戏规则是：在一个不透明的袋子里装有除数字以外其它均相同的4个小球，上面分别标有数字1、2、3、4．一人先从袋中随机摸出一个小球，另一人再从袋中剩下的3个小球中随机摸出一个小球．若摸出的两个小球上的数字和为奇数，则小明先挑选；否则小亮先挑选．‎ ‎（1）用树状图或列表法求出小明先挑选的概率；‎ ‎（2）你认为这个游戏公平吗？请说明理由．‎ ‎【关键词】列举法，树形图；频率估计概率；概率的应用 ‎【答案】解：（1）根据题意可列表或树状图如下：‎ ‎ 第一次 第二次 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎1‎ ‎——‎ ‎（1，2）‎ ‎（1，3）‎ ‎（1，4）‎ ‎2‎ ‎（2，1）‎ ‎——‎ ‎（2，3）‎ ‎（2，4）‎ ‎3‎ ‎（3，1）‎ ‎（3，2）‎ ‎——‎ ‎（3，4）‎ ‎4‎ ‎（4，1）‎ ‎（4，2）‎ ‎（4，3）‎ ‎——‎ ‎（1，2）‎ ‎（1，3）‎ ‎（1，4）‎ ‎2‎ ‎3‎ ‎4‎ ‎1‎ ‎（1，1）‎ ‎（2，3）‎ ‎（2，4）‎ ‎1‎ ‎3‎ ‎4‎ ‎2‎ ‎（3，1）‎ ‎（3，2）‎ ‎（3，4）‎ ‎1‎ ‎2‎ ‎4‎ ‎3‎ ‎（4，1）‎ ‎（4，2）‎ ‎（4，3）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ 第一次摸球 第二次摸球 从表或树状图可以看出所有可能结果共有12种，且每种结果发生的可能性相同，符合条件的结果有8种，‎ ‎∴（和为奇数）‎ ‎（2）不公平．‎ ‎∵小明先挑选的概率是（和为奇数），小亮先挑选的概率是（和为偶数），‎ ‎∵，∴不公平．‎