2010中考数学福州考试试题 8页

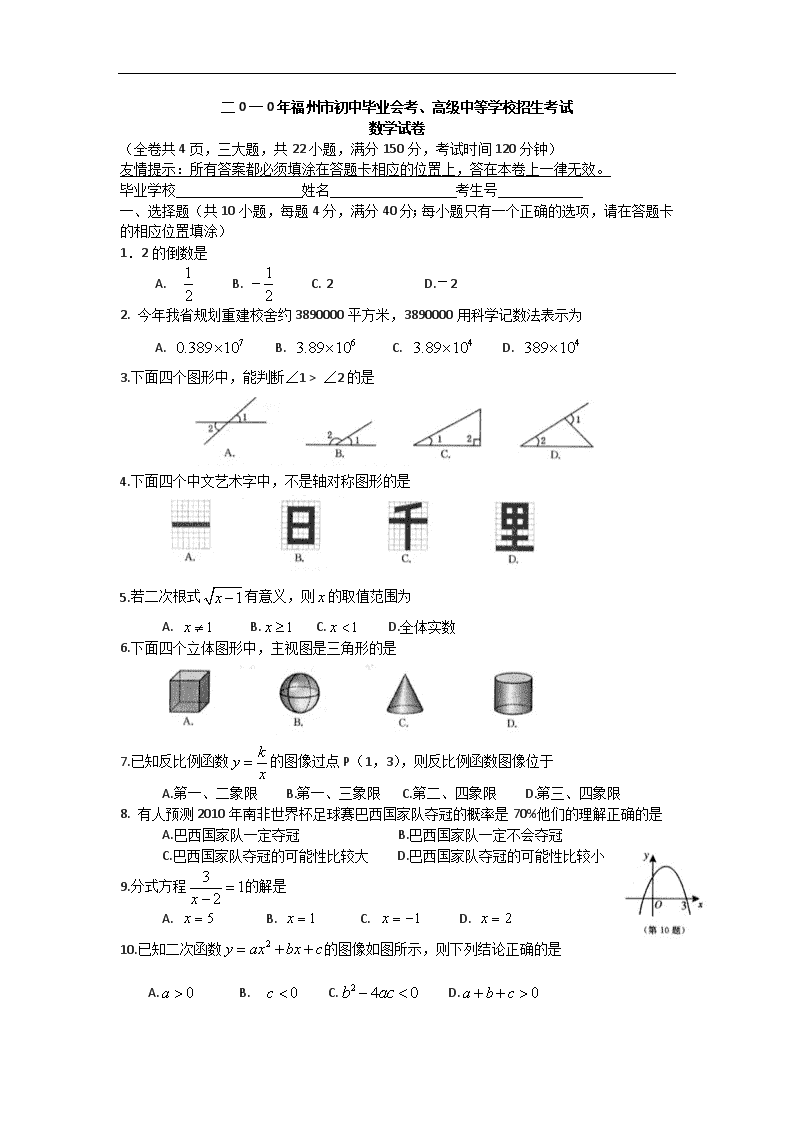
二0一0年福州市初中毕业会考、高级中等学校招生考试 数学试卷 ‎（全卷共4页，三大题，共22小题，满分150分，考试时间120分钟）‎ 友情提示：所有答案都必须填涂在答题卡相应的位置上，答在本卷上一律无效。‎ 毕业学校 姓名 考生号 ‎ 一、选择题（共10小题，每题4分，满分40分；每小题只有一个正确的选项，请在答题卡的相应位置填涂）‎ ‎1．2的倒数是 A. B. C. 2 D.－2‎ ‎2. 今年我省规划重建校舍约3890000平方米，3890000用科学记数法表示为 A. B. C. D. ‎ ‎3.下面四个图形中，能判断∠1 > ∠2的是 ‎4.下面四个中文艺术字中，不是轴对称图形的是 ‎ ‎ ‎5.若二次根式有意义，则的取值范围为 A. B. C. D.全体实数 ‎6.下面四个立体图形中，主视图是三角形的是 ‎7.已知反比例函数的图像过点P（1，3），则反比例函数图像位于 A.第一、二象限 B.第一、三象限 C.第二、四象限 D.第三、四象限 ‎8. 有人预测2010年南非世界杯足球赛巴西国家队夺冠的概率是70%他们的理解正确的是 A.巴西国家队一定夺冠 B.巴西国家队一定不会夺冠 C.巴西国家队夺冠的可能性比较大 D.巴西国家队夺冠的可能性比较小 ‎9.分式方程的解是 A. B. C. D. ‎ ‎10.已知二次函数的图像如图所示，则下列结论正确的是 A. B. C. D.‎ 二、填空题（共5小题，每题4分，满分20分。请将答案填入答题卡相应的位置）‎ ‎11.实数、在数轴上对应点的位置如图所示，则 （填“>”、“<”或“=”）。‎ ‎12.因式分解：= 。‎ ‎13.某校七年（2班）6位女生的体重（单位：千克）是：36，38，40，42，42，45，这组数据的众数为 。‎ ‎14.如图，在□ABCD中，对角线AC、BD相交于点O，若AC=14，BD=8，AB=10，则△OAB的周长为 。‎ ‎15.如图，直线，点坐标为（1，0），过点作的垂线交直线于点B，以原点O为圆心，长为半径画弧交轴于点；再过点的垂线交直线于点，以原点O为圆心，长为半径画弧交轴于点，…，按此做法进行下去，点的坐标为（ ， ）。‎ 三解答题（满分90分。请将答案填入答题卡的相应位置）‎ ‎16.（每小题7分，共14分）‎ ‎（1）计算：‎ ‎（2）化简：‎ ‎17.（每题7分，共14分）‎ ‎（1）如图，点B、E、C、F在一条直线上，BC=EF，AB∥DE，∠A=∠D。‎ 求证：△ABC≌△DEF。‎ ‎（2）如图，在矩形OABC中，点B的坐标为（－2，3）。画出矩形OABC绕点O顺时针旋转90°后的矩形OA1B1C1,并直接写出的坐标A1、B1、C1的坐标。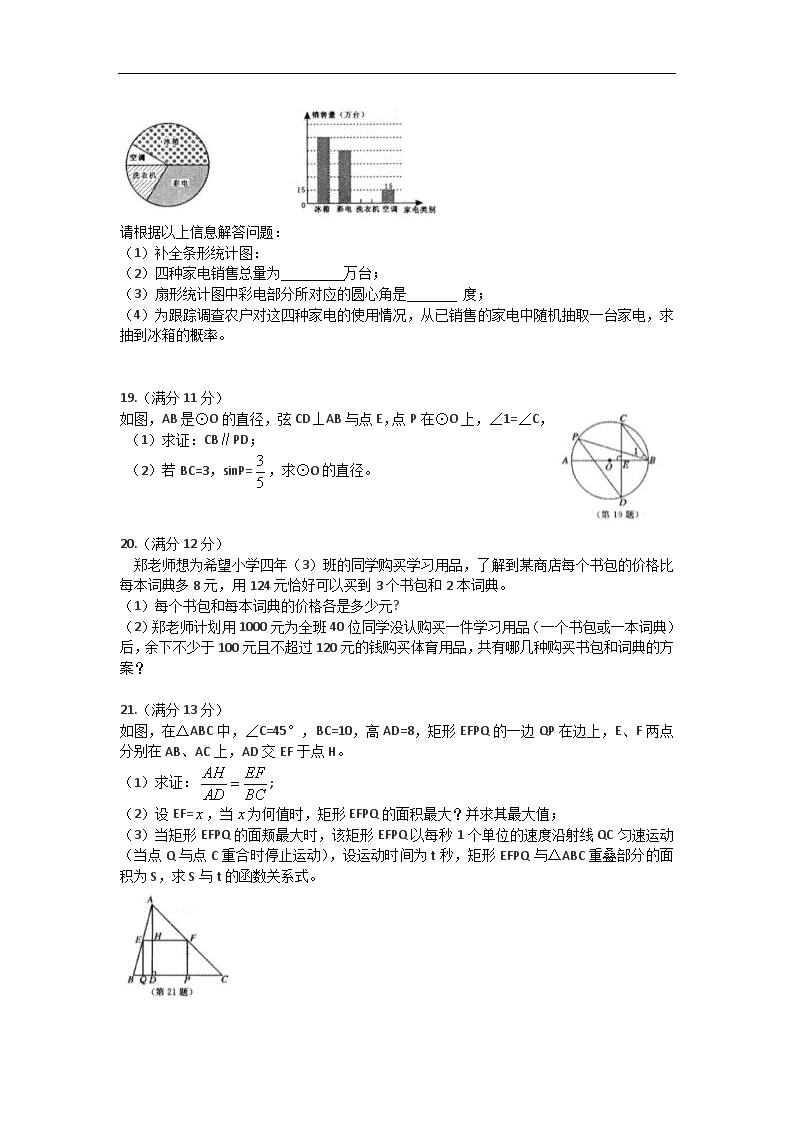‎ ‎18.（满分12分）‎ ‎ 近日从省家电下乡联席办获悉，自2009年2月20日我省家电下乡全面启动以来，最受农户热捧的四种家电是冰箱、彩电、洗衣机和空调，其销售比为5：4：2：1，其中空调已销售了15万台。根据上述销售情况绘制了两个不完整的统计图：‎ 请根据以上信息解答问题：‎ ‎（1）补全条形统计图：‎ ‎（2）四种家电销售总量为 万台；‎ ‎（3）扇形统计图中彩电部分所对应的圆心角是 度；‎ ‎（4）为跟踪调查农户对这四种家电的使用情况，从已销售的家电中随机抽取一台家电，求抽到冰箱的概率。‎ ‎19.（满分11分）‎ 如图，AB是⊙O的直径，弦CD⊥AB与点E，点P在⊙O上，∠1=∠C，‎ ‎ （1）求证：CB∥PD；‎ ‎（2）若BC=3，sinP=，求⊙O的直径。‎ ‎20.（满分12分）‎ ‎ 郑老师想为希望小学四年（3）班的同学购买学习用品，了解到某商店每个书包的价格比每本词典多8元，用124元恰好可以买到3个书包和2本词典。‎ ‎（1）每个书包和每本词典的价格各是多少元?‎ ‎（2）郑老师计划用1000元为全班40位同学没认购买一件学习用品（一个书包或一本词典）后，余下不少于100元且不超过120元的钱购买体育用品，共有哪几种购买书包和词典的方案？‎ ‎21.（满分13分）‎ 如图，在△ABC中，∠C=45°，BC=10，高AD=8，矩形EFPQ的一边QP在边上，E、F两点分别在AB、AC上，AD交EF于点H。‎ ‎（1）求证：;‎ ‎（2）设EF=，当为何值时，矩形EFPQ的面积最大？并求其最大值；‎ ‎（3）当矩形EFPQ的面颊最大时，该矩形EFPQ以每秒1个单位的速度沿射线QC匀速运动（当点Q与点C重合时停止运动），设运动时间为t秒，矩形EFPQ与△ABC重叠部分的面积为S，求S与t的函数关系式。‎ ‎22.（满分14分）‎ 如图1，在平面直角坐标系中，点B在直线上，过点B作轴的垂线，垂足为A，OA=5。若抛物线过点O、A两点。‎ ‎（1）求该抛物线的解析式；‎ ‎（2）若A点关于直线的对称点为C，判断点C是否在该抛物线上，并说明理由；‎ ‎（3）如图2，在（2）的条件下，⊙O1是以BC为直径的圆。过原点O作O1的切线OP，P为切点（P与点C不重合），抛物线上是否存在点Q，使得以PQ为直径的圆与O1相切？若存在，求出点Q的横坐标；若不存在，请说明理由。‎