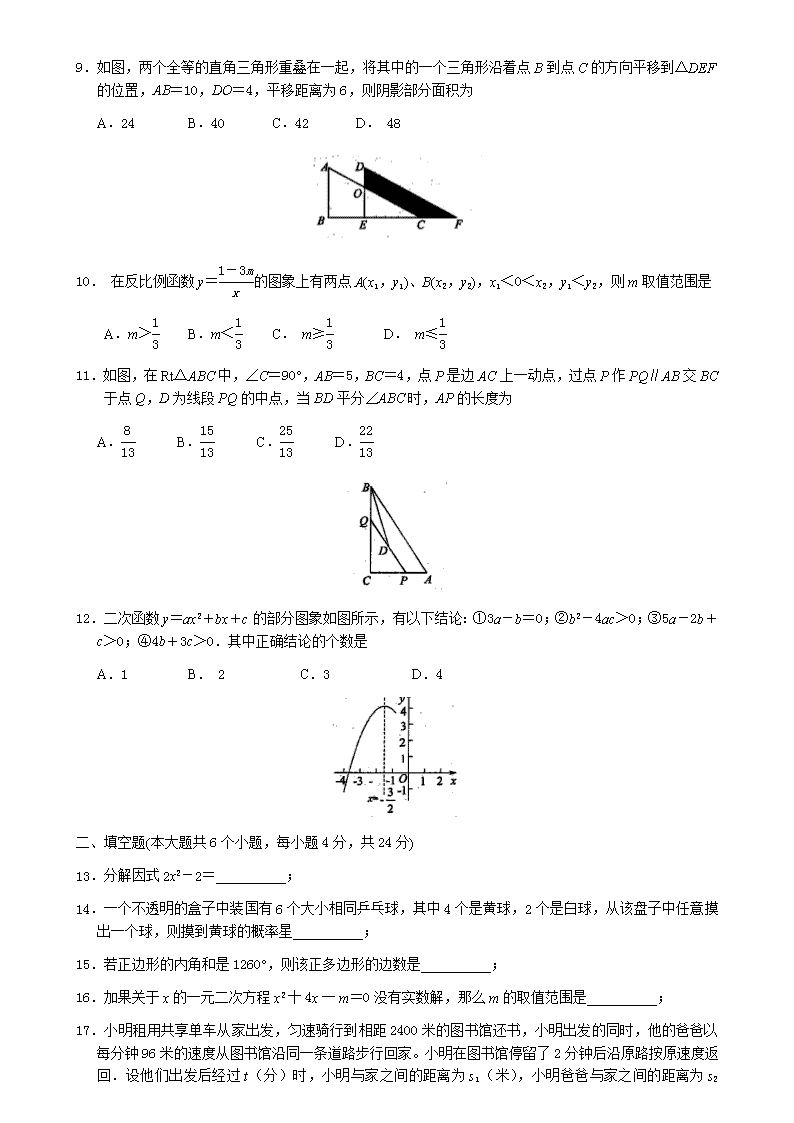2020年济南市天桥区九年级一模 数学试题 7页

‎2020年济南市天桥区九年级一模 数学试题 一、选择题(本大题共12个小题，每小题4分，月4分，在每小题结出的四个选项中，只有一项是符合题目要求．)‎ ‎1． －2的绝对值是 A．2 B． －2 C． D．－ ‎2．下列几何体中，的视图为三角形的是 ‎3．数字58500用科学记数法表示为 A．5.85×103 B．5.85×104 C．5.85×10－4 D．58.5×103‎ ‎4．如图，已知直线a∥b，直线c与直线a、b分别交于点A、B．∠1＝54°，则∠2＝‎ A．126° B．134° C．136° D．144°‎ ‎5．下列计算正确的是 A．（a－1)2＝a2－2a－1 B．2a(a－1)＝2a2－1 ‎ C．(a＋1)(a－1)＝a2－1 D．(a＋2)(a－1)＝a2－a－1‎ ‎6．下列图悉中， 既是随对称图形又是中心对称图形的是 ‎7．方程＝的解的是 ‎ A．x＝6　　　B．x＝7　　　C．x＝8　　　D．x＝－8‎ ‎8．某校举行汉字听写比赛，5个班级代表队正确答题数如图，这5个正确答题数的中位数和众数分别是 A．10， 15 B．13， 15 C．13，20 D．15， 15‎ ‎9．如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B到点C的方向平移到△DEF的位置，AB＝10，DO＝4，平移距离为6，则阴影部分面积为 A．24 B．40 C．42 D． 48‎ ‎10． 在反比例函数y＝的图象上有两点A(x1，y1)、B(x2，y2)，x1＜0＜x2，y1＜y2，则m取值范围是 A．m＞ B．m＜ C． m≥ D． m≤ ‎11．如图，在Rt△ABC中，∠C＝90°，AB＝5，BC＝4，点P是边AC上一动点，过点P作PQ∥AB交BC于点Q，D为线段PQ的中点，当BD平分∠ABC时，AP的长度为 ‎ A．　　　B．　　　C．　　　D． ‎12．二次函数y＝ax2＋bx＋c的部分图象如图所示，有以下结论：①3a－b＝0；②b2－4ac＞0；③5a－2b＋c＞0；④4b＋3c＞0．其中正确结论的个数是 A．1 B． 2 C．3 D．4‎ 二、填空题(本大题共6个小题，每小题4分，共24分)‎ ‎13．分解因式2x2－2＝__________；‎ ‎14．一个不透明的盒子中装国有6个大小相同乒乓球，其中4个是黄球，2个是白球，从该盘子中任意摸出一个球，则摸到黄球的概率星__________；‎ ‎15．若正边形的内角和是1260°，则该正多边形的边数是__________；‎ ‎16．加果关于x的一元二次方程x2十4x一m＝0没有实数解，那么m的取值范围是__________；‎ ‎17．小明租用共享单车从家出发，匀速骑行到相距2400米的图书馆还书，小明出发的同时，他的爸爸以每分钟96米的速度从图书馆沿同一条道路步行回家。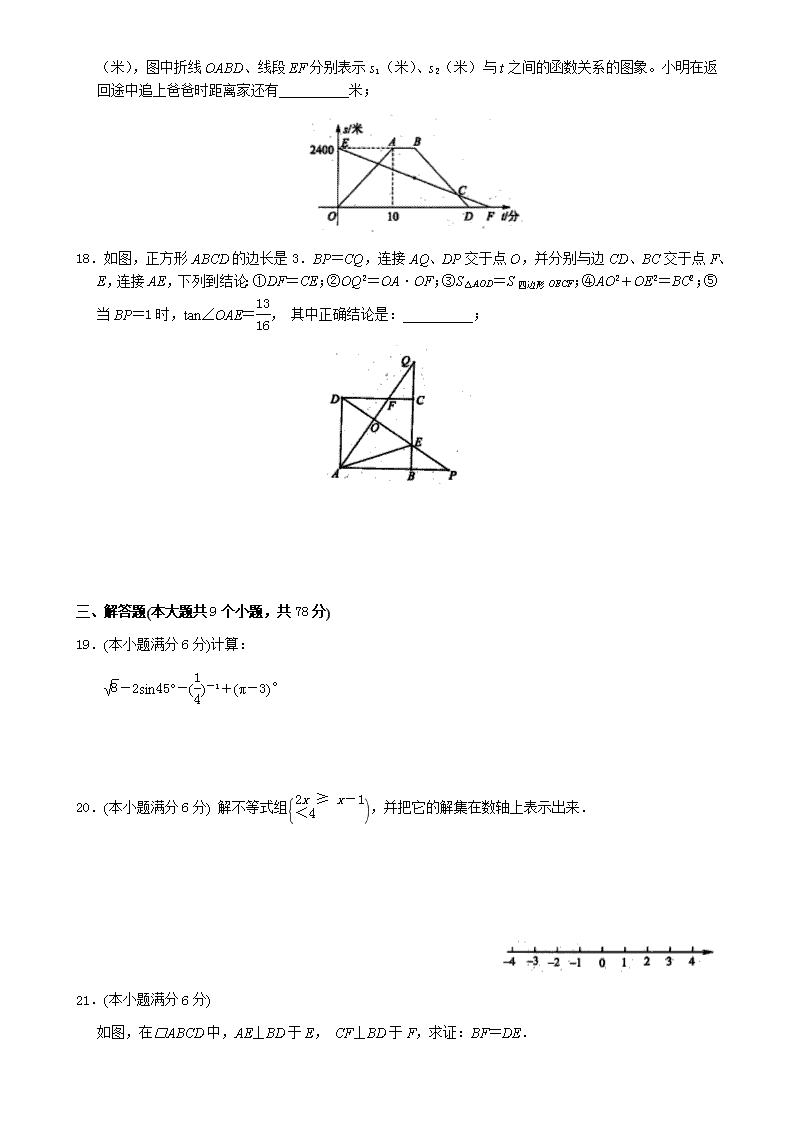小明在图书馆停留了2分钟后沿原路按原速度返回．设他们出发后经过t（分）时，小明与家之间的距离为s1（米），小明爸爸与家之间的距离为s2‎ ‎（米），图中折线OABD、线段EF分别表示s1（米）、s2（米）与t之间的函数关系的图象。小明在返回途中追上爸爸时距离家还有__________米；‎ ‎18．如图，正方形ABCD的边长是3．BP＝CQ，连接AQ、DP交于点O，并分别与边CD、BC交于点F、E，连接AE，下列到结论：①DF＝CE；②OQ2＝OA·OF；③S△AOD＝S四边形OECF；④AO2＋OE2＝BC2；⑤当BP＝1时，tan∠OAE＝， 其中正确结论是：__________；‎ 三、解答题(本大题共9个小题，共78分)‎ ‎19．(本小题满分6分)计算：‎ －2sin45°－()－1＋(π－3)°‎ ‎20．(本小题满分6分) 解不等式组，并把它的解集在数轴上表示出来．‎ ‎21．(本小题满分6分)‎ 如图，在□ABCD中，AE⊥BD于E， CF⊥BD于F，求证：BF＝DE．‎ ‎22．(本小题满分8分)‎ 甲、乙两个药业集团共有药品库存50吨，为抗击疫情支援灾区，甲集团捐赠出60%库存的药品，乙集团捐赠出40%库存的药品，组织车辆连夜送往抗疫最前线．若两个药业集团所捐赠的药品数量相同，那么甲，乙两药业集团原来各自的药品库存量有多少吨?‎ ‎23．(本小题满分8分)‎ 如图，Rt△ABC中，∠C＝90°，点O在边AB上，以O点为圆心、OB为半径作圆，分别与BC、AB相交于点D、E，连结AD，AD是⊙O的切线．‎ ‎(1)求证：∠CAD＝∠B；‎ ‎(2)若BC＝4， tanB＝， 求⊙O半径．‎ ‎24． (本小题满分10分)‎ 某市少年宫为小学生开设了绘画、音乐、舞蹈和跆拳道四类兴趣班，为了解学生对这四类兴趣班的喜爱情况，对学生进行了随机问卷调查(问卷调查表如下表所示)，将调查结果整理后绘制了一幅不完整的统计表：‎ ‎(1)统计表中的a＝__________，b＝__________；‎ ‎(2)根据调查结果，请你估计该市2000名小学生中最喜欢“绘画”兴趣班的人数；‎ ‎(3)王姝和李要选择参加兴趣班，若他们每人从A、 B、C、D四类兴趣班中随机选取一类，请用画树状图或列表格的方法，求两人恰好选中同一类的概率．‎ ‎25． (本小题满分10分)‎ 如图1，在平面直角坐标系中，放置有一个Rt△ABC，顶点A与原点O重合，边AC与x轴重合，‎ ‎∠ACB＝90°，AC＝BC＝4，反比例函数y＝的图象分别与AB和BC交于点D、E，且此时点D恰为AB的中点．‎ ‎(1)求反比例函数的表达式及点E的坐标；‎ ‎(2)连接DE，在x轴上存在一点P，可使得△DEP成为以DE为腰的等腰三角形，试求出所有符合条件的点P的坐标；‎ ‎(3)如图2，保持反比例函数图象不变，将△ABC沿x轴向左平移，使得点E成为BC的中点，求此时点D的坐标．‎ ‎26． (本小题满分12分)‎ ‎[问题引入]‎ ‎(1)如图1，在正方形ABCD中，E、F分别是BC、CD两边上的点，且AE⊥BF，垂足为点P．求证： AE＝BF；‎ ‎[类比探究]‎ ‎(2)如图2，把(1)中正方形ABCD改为矩形ABCD，且AD＝2AB，其余条件不变，请你推断AE、BF满足怎样的数量关系，并说明你的理由；‎ ‎[实践应用]‎ ‎(3)如图3， Rt△ABC中，∠BAC＝30°，把△ABC沿斜边AC对折得到Rt△ADC，E、 F分别为CD、 AD边上的点，连接AE、 BF，恰好使得AE⊥BF，垂足为点P．请求出的值．‎ ‎27． (本小题满分12分)‎ 如图，已知抛物线y＝ ax2＋bx＋c (a≠0)与x轴交于A (－1， 0)， B(3， 0)两点，与y轴交于点C (0， 3)． 点D是抛物线的顶点，点E (n， 3)在抛物线上，设直线AE上方的抛物线上的动点P的横坐标为m．‎ ‎(1)求该抛物线的解析式及顶点D的坐标；‎ ‎(2)连接PA、 PE，当m为何值时S△APE＝S△ABE?‎ ‎(3)过点P作PH∥AB交直线AE于点H，再作HG∥PA交AB于点G，那么当OG最大时，请求出点P的坐标．‎