2019年山东青岛中考数学试题（解析版） 18页

‎{来源}2019年山东青岛中考数学试卷 ‎{适用范围:3． 九年级}‎ ‎{标题}2019年山东省青岛市中考数学试卷 考试时间：120分钟 满分：120分 ‎{题型:1-选择题}一、选择题：本大题共 小题，每小题 分，合计分． ‎ ‎{题目}1．（2019年青岛）－的相反数是（ ）‎ A．－ B．- C．± D．‎ ‎{答案}D ‎{解析}本题考查了相反数的定义，绝对值相等、符号不同的两个数互为相反数，由于－的相反数是，因此本题选D．‎ ‎{分值}3‎ ‎{章节:[1-1-2-3]相反数}‎ ‎{考点:相反数的定义}‎ ‎{类别:常考题}‎ ‎{难度:1-最简单}‎ ‎{题目}2．（2019年青岛）下列四个图形中，既是轴对称图形，又是中心对称图形的是（ ）‎ ‎ A. B. C. D.‎ ‎ ‎ ‎{答案}D ‎{解析}本题考查了轴对称图形和中心对称图形的识别，轴对称图形是沿直线对折后直线两旁的部分能够重合的图形，中心对称图形是绕某点旋转180°后能与自身重合的图形，正确区分这两类图形是解题的关键. 选项A，C，D中的图形都是轴对称图形，选项B，D中的图形都是中心对称图形，故选项B中的图形既是轴对称图形也是中心对称图形，因此本题选B．‎ ‎{分值}3‎ ‎{章节:[1-23-2-2]中心对称图形}‎ ‎{考点:轴对称图形}‎ ‎{考点:中心对称图形}‎ ‎{类别:常考题}‎ ‎{难度:2-简单}‎ ‎{题目}3．（2019年青岛）2019 年 1 月 3 日，我国“嫦娥四号”月球探测器在月球背面软着陆，实现人类有史以来首次成功登陆月球背面．已知月球与地球之间的平均距离约为 384 000km，把 384 000km用科学记数法可以表示为（ ）‎ A．38.4×104 km B．3.84×105 km C．0.384×106 km D．3.84×106 km ‎ ‎{答案}B ‎{解析}本题考查了用科学记数法表示较大的数，将一个数表示为a×10n的形式时，注意1≤a＜10. 384 000＝384×103＝3.84×102×103＝3.84×105，因此本题选B．‎ ‎{分值}3‎ ‎{章节:[1-1-5-2]科学计数法}‎ ‎{考点:将一个绝对值较大的数科学计数法}‎ ‎{类别:常考题}‎ ‎{难度:1-最简单}‎ ‎{题目}4．（2019年青岛）计算（－2m）2·（－m·m2＋3m3）的结果是（ ）‎ A．8m5 B．-8m5 C．8m6 D．-4m4＋12m5‎ ‎{答案}A ‎{解析}本题考查了整式的运算，掌握积的乘方、合并同类项、多项式乘多项式等运算法则是解题的关键，解题注意不要混淆幂的几个运算性质而出错.原式＝4m2·（－m3＋3m3）＝4m2·2m3＝8m5，因此本题选A．‎ ‎{分值}3‎ ‎{章节:[1-14-1]整式的乘法}‎ ‎{考点:积的乘方}‎ ‎{考点:整式加减}‎ ‎{考点:单项式乘以多项式}‎ ‎{考点:同底数幂的乘法}‎ ‎{类别:常考题}‎ ‎{难度:2-简单}‎ ‎{题目}5．（2019年青岛）如图，线段 AB 经过⊙O 的圆心， AC ， BD 分别与⊙O 相切于点 C ， D ．若 AC＝BD＝4 ，∠A＝45 °，则弧CD的长度为（ ）‎ ‎ A．p B．2p C．2p D．4p ‎{答案}B ‎{解析}本题考查了圆的切线的性质、等腰直角三角形的判定和性质、弧长的计算，先根据“圆的切线垂直于经过切点的半径”可得到直角三角形，再根据“等角对等边”可得到等腰三角形，最后根据公式计算弧长.如图，连接OC，OD.∵AC ， BD 分别与⊙O 相切于点 C ， D，∴AC⊥OC，BD⊥OD，∴∠ACO＝∠BDO＝90°.∵∠A＝45°，∴∠AOC＝45°，∴∠A＝∠AOC，∴OC＝AC＝4.∵AC＝BD，OC＝OD，∴OD＝BD，∴∠DOB＝∠B＝45°，∴∠COD＝180°－45°－45°＝90°.∴.因此本题选B．‎ ‎{分值}3‎ ‎{章节:[1-24-4]弧长和扇形面积}‎ ‎{考点:三角形内角和定理}‎ ‎{考点:等角对等边}‎ ‎{考点:切线的性质}‎ ‎{考点:弧长的计算}‎ ‎{类别:常考题}‎ ‎{难度:3-中等难度}‎ ‎{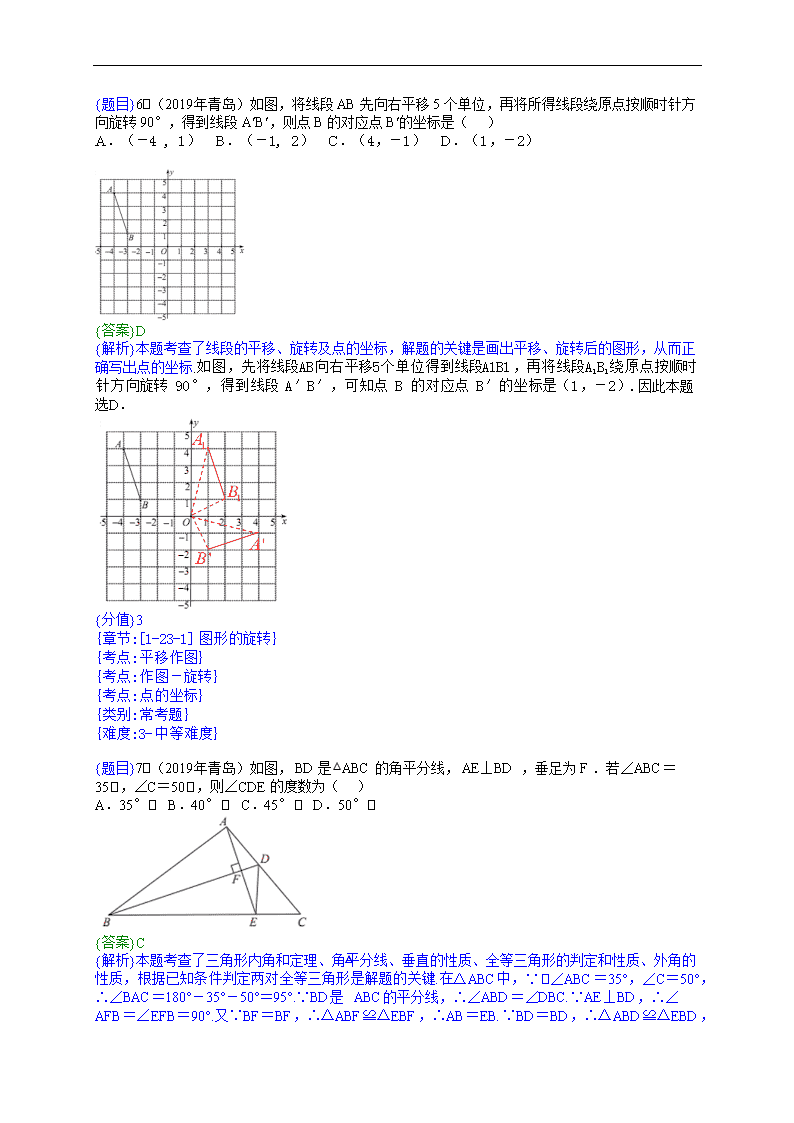题目}6．（2019年青岛）如图，将线段 AB 先向右平移 5 个单位，再将所得线段绕原点按顺时针方向旋转 90°，得到线段 A¢B¢，则点 B 的对应点 B¢的坐标是（ ）‎ A．（－4 , 1） B．（－1, 2） C．（4，－1） D．（1，－2）‎ ‎{答案}D ‎{解析}本题考查了线段的平移、旋转及点的坐标，解题的关键是画出平移、旋转后的图形，从而正确写出点的坐标.如图，先将线段AB向右平移5个单位得到线段A1B1，再将线段A1B1绕原点按顺时针方向旋转 90°，得到线段 A′B′，可知点 B 的对应点 B′的坐标是（1，－2）.因此本题选D．‎ ‎{分值}3‎ ‎{章节:[1-23-1]图形的旋转}‎ ‎{考点:平移作图}‎ ‎{考点:作图－旋转}‎ ‎{考点:点的坐标}‎ ‎{类别:常考题}‎ ‎{难度:3-中等难度}‎ ‎{题目}7．（2019年青岛）如图， BD 是△ABC 的角平分线， AE⊥BD ，垂足为 F ．若∠ABC＝35°，∠C＝50°，则∠CDE 的度数为（ ）‎ A．35°° B．40°° C．45°° D．50°° ‎{答案}C ‎{解析}本题考查了三角形内角和定理、角平分线、垂直的性质、全等三角形的判定和性质、外角的性质，根据已知条件判定两对全等三角形是解题的关键.在△ABC中，∵Ð∠ABC＝35°，∠C＝50°，∴∠BAC＝180°－35°－50°＝95°.∵BD是△ABC的平分线，∴∠ABD＝∠DBC.∵AE⊥BD，∴∠AFB＝∠EFB＝90°.又∵BF＝BF，∴△ABF≌△EBF，∴AB＝EB.∵BD＝BD，∴△ABD≌△EBD，‎ ‎∴∠DEB＝∠BAC＝95°.∵∠DEB是△DEC的外角，∴∠CDE＝∠DEB－∠C＝95°－50°＝45°.，因此本题选C．‎ ‎{分值}3‎ ‎{章节:[1-12-2]三角形全等的判定}‎ ‎{考点:三角形的角平分线}‎ ‎{考点:三角形内角和定理}‎ ‎{考点:全等三角形的判定SAS}‎ ‎{考点:三角形的外角}‎ ‎{类别:常考题}‎ ‎{难度:3-中等难度} ‎ ‎{题目}8．（2019年青岛）已知反比例函数 y＝的图象如图所示，则二次函数 y＝ax 2－2x和一次函数 y＝bx＋a 在同一平面直角坐标系中的图象可能是（ ）‎ ‎ A. B. C. D.‎ ‎{答案}C ‎{解析}本题考查了反比例函数和二次函数的图像.对于反比例函数y＝，当k＞0时，其图像的两个分支分为位于第一、三象限；当k＜0时，其图像的两个分支分为位于第二、四象限.对于二次函数y＝ax2＋bx＋c，当a＞0时，其图像的开口向上；当a＜0时，其图像的开口向下.当a，b同号时，对称轴－＜0，其图像的对称轴在y轴左侧；当a，b异号时，对称轴－＞0，其图像的对称轴在y轴右侧.∵反比例函数 y＝的图像位于第一、三象限，∴ab＞0，即a,b同号.对于二次函数y＝ax2－2x，当x＝0时，y＝0，即它的图像经过原点，故不能是选项A中的图像.当a＞0，b＞0时，二次函数y＝ax2－2x的图像开口向上，对称轴x＝＞0，即对称轴在y轴右侧，一次函数y＝bx＋a的图像经过第一、二、三象限，故不可能是选项B中的图像，可能是选项C中的图像；当a＜0，b＜0时，二次函数y＝ax2－2x的图像开口向下，对称轴x＝＜0，即对称轴在y轴左侧，一次函数y＝bx＋a的图像经过第二、三、四象限，故不可能是选项D中的图像，因此本题选C．‎ ‎{分值}3‎ ‎{章节:[1-22-1-4]二次函数y＝ax2＋bx＋c的图象和性质}‎ ‎{考点:反比例函数的图象}‎ ‎{考点:二次函数y＝ax2＋bx＋c的性质}‎ ‎{类别:常考题}‎ ‎{难度:4-较高难度}‎ ‎{题型:2-填空题}二、填空题：本大题共6小题，每小题3分，合计18分．‎ ‎{题目}9．（2019年青岛）计算：＝ .‎ ‎{答案}2＋1‎ ‎{解析}本题考查了二次根式的运算及零指数幂，根据二次根式的运算法则和零指数幂的性质计算即可，原式＝，因此本题答案为2＋1．‎ ‎{分值}3‎ ‎{章节:[1-16-3]二次根式的加减}‎ ‎{考点:二次根式的混合运算}‎ ‎{考点:零次幂}‎ ‎{类别:常考题}‎ ‎{难度:2-简单}‎ ‎{题目}10．（2019年青岛）若关于 x 的一元二次方程2x2－x＋m＝0有两个相等的实数根，则 m 的值为 .‎ ‎{答案}‎ ‎{解析}本题考查了一元二次方程根的情况与根的判别式b2－4ac的关系，即当b2－4ac＞0时，方程有两个不相等的实数根；当b2－4ac＝0时，方程有两个相等的实数根；当b2－4ac＜0时，方程没有实数根. ∵关于 x 的一元二次方程2x2－x＋m＝0有两个相等的实数根，∴b2－4ac＝0，即（－1）2－4×2×m＝0，解得m＝.因此答案为．‎ ‎{分值}3‎ ‎{章节:[1-21-2-2]公式法}‎ ‎{考点:根的判别式}‎ ‎{类别:常考题}‎ ‎{难度:2-简单}‎ ‎{题目}11．（2019年青岛）射击比赛中，某队员 10 次射击成绩如图所示，则该队员的平均成绩是 环．‎ ‎{答案}8.5‎ ‎{解析}本题考查了条形统计图和算术平均数的计算，解题的关键是看懂统计图中的数据和正确计算.×（6×1＋7×1＋8×2＋9×4＋10×2）＝×85＝8.5，即该队员的平均成绩是8.5环，因此本题答案为8.5．‎ ‎{分值}3‎ ‎{章节:[1-20-1-1]平均数}‎ ‎{考点:条形统计图}‎ ‎{考点:算术平均数}‎ ‎{类别:常考题}‎ ‎{难度:2-简单}‎ ‎{题目}12．（2019年青岛）如图，五边形 ABCDE 是⊙O 的内接正五边形， AF 是⊙O 的直径，则 ÐBDF 的度数是 °．‎ ‎{答案}54‎ ‎{解析}本题考查了圆内接正多边形的性质、圆周角定理及其推论，即圆内接正n边形的中心角等于，同弧所对的圆周角等于圆心角的一半，直径所对的圆周角是直角.如图，连接AD.∵AF是⊙O 的直径，∴∠ADF＝90°.∵五边形 ABCDE 是⊙O 的内接正五边形，∴∠AOB＝360°÷5＝72°，∴∠ADB＝×72°＝36°.∴∠BDF＝90°－36°＝54°，因此本题答案为54．‎ ‎{分值}3‎ ‎{章节:[1-24-3]正多边形和圆}‎ ‎{考点:正多边形和圆}‎ ‎{考点:圆周角定理}‎ ‎{考点:直径所对的圆周角}‎ ‎{类别:常考题}‎ ‎{难度:3-中等难度}‎ ‎{题目}13．（2019年青岛）如图，在正方形纸片 ABCD 中， E 是 CD 的中点，将正方形纸片折叠，点 B 落在线段AE 上的点 G 处，折痕为 AF ．若 AD＝4 cm，则 CF 的长为 cm ．‎ ‎{答案}6-2‎ ‎{解析}本题是一道折叠问题，考查了轴对称的性质、正方形的性质、勾股定理等知识，解题的关键根据折叠的性质得到相等的线段，进而根据勾股定理列方程求解.∵E是CD的中点，CD＝AD＝4，∴DE＝CE＝2.在Rt△ADE中，根据勾股定理，得AE＝.由折叠的性质可得△AGF≌△ABF，∴AG＝AB＝4,GF＝BF,∠AGF＝∠B＝90°.∴∠FGE＝90°，GE＝AE-AG＝设BF＝‎ x，则GF＝x，FC＝4-x.在Rt△GEF中，根据勾股定理，得EF2＝GE2＋GF2＝在Rt△CEF中，根据勾股定理，得EF2＝CE2＋FC2＝∴，解得x＝6-2，因此本题答案为6-2． ‎ ‎{分值}3‎ ‎{章节:[1-18-2-3] 正方形}‎ ‎{考点:勾股定理}‎ ‎{考点:正方形有关的综合题}‎ ‎{考点:折叠问题}‎ ‎{类别:常考题} ‎ ‎{难度:4-较高难度}‎ ‎{题目}14．（2019年青岛）如图，一个正方体由 27 个大小相同的小立方块搭成，现从中取走若干个小立方块，得到一个新的几何体．若新几何体与原正方体的表面积相等，则最多可以取走 ‎ 个小立方块．‎ ‎{答案}16‎ ‎{解析}本题考查了几何体的三视图，解题的关键是具有较好的空间想象能力.当至少剩下9个小立方块时新几何体与原正方体的表面积相等，故最多可以取走27-9＝16个小立方块，因此本题答案为16．‎ ‎{分值}3‎ ‎{章节:[1-29-2]三视图}‎ ‎{考点:简单组合体的三视图}‎ ‎{类别:高度原创}‎ ‎{类别:易错题}‎ ‎{难度:5-高难度}‎ ‎{题型:4-解答题}三、解答题：本大题共 小题，合计分．‎ ‎{题目}15．（2019年青岛）已知： ∠α，直线 l 及 l 上两点 A， B．‎ 求作： Rt△ABC ，使点 C 在直线 l 的上方，且∠ABC＝90°， ∠BAC＝∠α．‎ ‎{解析}本题考查了尺规作图，掌握用尺规作一个角等于已知角，过直线上一点作这条直线的垂线是解题的关键.如图，在直线l上方作∠BAD＝∠α，过点B作直线EF⊥l，交BD于点C，则△ABC即为所求.‎ ‎……4分 ‎{答案}解： ‎ ‎{分值}4‎ ‎{章节:[1-13-1-2]垂直平分线}‎ ‎{难度:2-简单}‎ ‎{类别:常考题}‎ ‎{考点:与全等有关的作图问题}‎ ‎{考点:与垂直平分线有关的作图}‎ ‎{题目}16（1）．（2019年青岛）化简：；‎ ‎{解析}本题考查了分式的混合运算，按照先计算括号内的加法，再计算除法进行运算．‎ ‎{答案}解： 原式＝＝＝‎ ‎＝＝. ‎ ‎{分值}4‎ ‎{章节:[1-15-2-2]分式的加减}‎ ‎{难度:2-简单}‎ ‎{类别:常考题} ‎ ‎{考点:分式的混合运算}‎ ‎{题目}16（2）．（2019年青岛）解不等式组 ，并写出它的正整数解．‎ ‎{解析}本题考查了不等组的解法和不等式组的整数解，解不等式组的步骤为：先解出不等式组中每个不等式的解集，然后在数轴上分别表示出两个解集，找出公共部分，得出不等式组的解集．‎ ‎{答案}解： 解不等式1－x≤，得x≥－1；‎ 解不等式3x－1＜8，得x＜3； ‎ ‎∴不等式组的解集为－1≤x＜3. ‎ ‎∴不等式组的正整数解为x＝1,2. ‎ ‎{分值}4‎ ‎{章节:[1-9-3]一元一次不等式组}‎ ‎{难度:2-简单}‎ ‎{类别:常考题}‎ ‎{考点:解一元一次不等式组}‎ ‎{考点:一元一次不等式组的整数解}‎ ‎{题目}17．（2019年青岛）小明和小刚一起做游戏，游戏规则如下：将分别标有数字 1， 2， 3， 4 的 4 个小球放入一个不透明的袋子中，这些球除数字外都相同．从中随机摸出一个球记下数字后放回，再从中随机摸出一个球记下数字．若两次数字差的绝对值小于 2，则小明获胜，否则小刚获胜．这个游戏对两人公平吗？请说明理由．‎ ‎{解析}本题考查了概率的求法，先列表或画树状图表示出所有可能的情形，进而求出小明胜和小刚胜的概率；再根据“如果两人获胜的概率相等，那么游戏对双方公平，否则不公平”作出判断.．‎ ‎{答案}解： 列表表示所有可能的结果为：‎ ‎ 第2个数字 ‎ 差的绝对值 第1个数字 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎2‎ ‎1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎2‎ ‎1‎ ‎0‎ ‎1‎ ‎4‎ ‎4‎ ‎2‎ ‎1‎ ‎0‎ 由上表可知，共有16种等可能的结果，其中两次数字差的绝对值小于 2的结果有10种，∴P（小明获胜）＝，P（小明获胜）＝. ‎ ‎∵P（小明获胜）≠P（小明获胜），∴这个游戏对两人不公平.‎ ‎{分值}6‎ ‎{章节:[1-25-2]用列举法求概率}‎ ‎{难度:2-简单}‎ ‎{类别:常考题}‎ ‎{考点:绝对值的意义}‎ ‎{考点:两步事件放回}‎ ‎{考点:游戏的公平性}‎ ‎{题目}18．（2019年青岛）为了解学生每天的睡眠情况，某初中学校从全校 800 名学生中随机抽取了 40 名学生，调查了他们平均每天的睡眠时间（单位： h） ，统计结果如下：‎ ‎9，8，10.5，7，9，8，10，9.5，8，9，9.5，7.5，9.5，9，8.5，7.5，10，9.5，8，9，‎ ‎7，9.5，8.5，9，7，9，9，7.5，8.5，8.5，9，8，7.5，9.5，10，9.5，8.5，9，8，9.‎ 在对这些数据整理后，绘制了如下的统计图表：‎ 睡眠时间分组统计表 睡眠时间分布情况 组别 ‎ 睡眠时间分组 ‎ 人数（频数）‎ ‎1 ‎ ‎7≤t＜8 ‎ m ‎2 ‎ ‎8≤t＜9 ‎ ‎11‎ ‎3 ‎ ‎9≤t＜10 ‎ n ‎4 ‎ ‎10≤t＜11 ‎ ‎4‎ 请根据以上信息，解答下列问题：‎ ‎（1） m＝ ， n＝ ， a＝ ， b＝ ；‎ ‎（2）抽取的这 40 名学生平均每天睡眠时间的中位数落在 组（填组别） ；‎ ‎（3）如果按照学校要求，学生平均每天的睡眠时间应不少于 9 h，请估计该校学生中睡 眠时间符合要求的人数．‎ ‎{解析}本题是一道统计综合题，考察了频数分布表、扇形统计图、中位数及用样本估计总体．（1）根据统计结果可知，睡眠时间在7≤t＜8范围的内有7人，故m＝7，∴n＝40-7-11-4＝18，a＝×100%＝17.5%，b＝×100%＝45%.（2）因为共有40个数据，所以中位数等于第20个数据和第21个数据的平均数.由统计表可知第20个数据和第21个数据都在第3组内，故中位数落在第3组.（3）利用样本去估计总体中睡眠时间符合要求的人数所占百分比.‎ ‎{答案}解： （1）7 18 17.5% 45%； ‎ ‎（2）3；‎ ‎（3）在抽取的这40名学生中平均每天的睡眠时间应不少于 9 h的学生人数所占百分比为45%＋10%＝55%，由此估计该校学生中睡眠时间符合要求的人数约为800×55%＝440（人）.‎ ‎{分值}6‎ ‎{章节:[1-20-1-2]中位数和众数}‎ ‎{难度:2-简单}‎ ‎{类别:常考题}‎ ‎{考点:扇形统计图}‎ ‎{考点:频数（率）分布表}‎ ‎{考点:用样本估计总体}‎ ‎{考点:频数与频率}‎ ‎{考点:中位数}‎ ‎{题目}19．（2019年青岛）如图，某旅游景区为方便游客，修建了一条东西走向的木栈道 AB ，栈道 AB 与景区道路CD 平行．在 C 处测得栈道一端 A 位于北偏西 42° 方向，在 D 处测得栈道另一端 B 位于北偏西 32°方向．已知 CD＝120 m ， BD＝80 m ，求木栈道 AB 的长度（结果保留整数） ．‎ ‎（参考数据：sin32°≈，cos32°≈，tan32°≈，sin42°≈，cos42°≈，tan42°≈）‎ ‎{解析}本题考查了解直角三角形的实际应用，做辅助线构造直角三角形是解题的关键．如图，过点C作CE⊥AB于E，过点D作DF⊥AB，交AB的延长线于点F，则四边形CDFE是矩形.在Rt△BDF中求出BF和DF的长，进而得到EB的长；在Rt△Rt△ACE中求出AE的长，进而根据AB＝AE＋EB求解.‎ ‎{答案}解： 如图，过点C作CE⊥AB于E，过点D作DF⊥AB，交AB的延长线于点F，∴CE∥DF.∵AB∥CD，∴四边形CDFE是矩形，∴EF＝CD＝120，CE＝DF.‎ 在Rt△BDF中，∵∠BDF＝32°，BD＝80，∴BF＝80·sin32°＝80×＝42.5，DF＝80·cos32°＝80×＝68.∴EB＝EF－BF＝120－42.5＝77.5. ‎ 在Rt△ACE中，∵CE＝DF＝68，∠ACE＝42°，∴AE＝68·tan42°＝68×＝61.2.∴AB＝AE＋EB＝61.2＋77.5≈139. 答：木栈道 AB 的长度约为139m. ‎ ‎{分值}6‎ ‎{章节:[1-28-1-2]解直角三角形}‎ ‎{难度:3-中等难度}‎ ‎{类别:常考题}‎ ‎{考点:矩形的性质}‎ ‎{考点:解直角三角形－方位角}‎ ‎{题目}20．（2019年青岛）甲、乙两人加工同一种零件，甲每天加工的数量是乙每天加工数量的 1.5 倍，两人各加工 600 个这种零件，甲比乙少用 5 天．‎ ‎（1）求甲、乙两人每天各加工多少个这种零件？‎ ‎（2）已知甲、乙两人加工这种零件每天的加工费分别是 150 元和 120 元，现有 3000 个 这种零件的加工任务，甲单独加工一段时间后另有安排，剩余任务由乙单独完 成．如果总加工费不超过 7800 元，那么甲至少加工了多少天？‎ ‎{解析}本题考查了列方程解决实际问题和列不等式解决实际问题，找出问题中的等量关系和不等关系是解题的关键．（1）根据“乙加工600个零件的时间－甲加工600个零件的时间＝5”列分式方程求解，不要遗漏检验；（2）根据“甲的加工费＋乙的加工费≤7800”列不等式求解.‎ ‎{答案}解： 解：（1）设乙每天加工x个零件，则甲每天加工1.5x个零件，根据题意，得 ‎，‎ 解这个方程，得x＝40.‎ 经检验，x＝40是原分式方程的根. ‎ ‎1.5x＝1.5×40＝60.‎ 答：甲每天加工60个零件，乙每天加工40个零件. ‎ ‎（2）设甲加工了x天，根据题意，得 ‎150x＋≤7800， ‎ 解这个不等式，得x≥40.‎ 答：甲至少加工了40天. ‎ ‎{分值}8‎ ‎{章节:[1-15-3]分式方程}‎ ‎{难度:3-中等难度}‎ ‎{类别:常考题}‎ ‎{考点:分式方程的应用（工程问题）}‎ ‎{考点:一元一次不等式的应用}‎ ‎{题目}21．（2019年青岛）如图，在□ABCD 中，对角线 AC 与 BD 相交于点 O ，点 E ， F 分别为 OB ， OD 的中点，延长 AE 至 G ，使 EG＝AE ，连接 CG ．‎ ‎（1）求证： △ABE≌△CDF ；‎ ‎（2）当 AB 与 AC 满足什么数量关系时，四边形 EGCF 是矩形？请说明理由.‎ ‎{解析}本题考查了平行四边形的性质、全等三角形的判定和性质、矩形的判定等知识，掌握以上图形的性质和判定方法是解题的关键．（1）根据平行四边形的性质可得到AB＝CD，∠ABE＝∠CDF，根据中点的定义可得到BE＝DF，进而根据SAS证得△ABE≌△CDF.（2）由△ABE≌△CDF可得到AE＝CF＝EG， AG∥CF，从而得到四边形EGCF是平行四边形.假设平行四边形 EGCF 是矩形，从而可得AE⊥BO，又有BE＝EO，则AB＝AO＝AC，即当AC＝2AB时，四边形EGCF是矩形.‎ ‎{答案}解：（1）证明：∵四边形ABCD是平行四边形，‎ ‎∴AB∥CD，AB＝CD，OB＝OD.‎ ‎∴∠ABE＝∠CDF. ‎ ‎∵点 E ， F 分别为 OB ， OD 的中点，∴BE＝DF.‎ ‎∴△ABE≌△CDF. ‎ ‎（2）当AC＝2AB时，四边形EGCF是矩形. ‎ ‎∵△ABE≌△CDF，‎ ‎∴AE＝CF，∠BAE＝∠DCF.‎ ‎∵EG＝AE，∴EG＝CF.‎ ‎∵AB∥CD，∴∠BAC＝∠DCA，‎ ‎∴∠GAC＝∠FCA，∴AG∥CF，‎ ‎∴四边形EGCF是平行四边形. ‎ ‎∵AC＝2AB，AC＝2AO，‎ ‎∴AB＝AO.‎ ‎∵点E是BO的中点，‎ ‎∴AE⊥BO，∴∠GEF＝90°，‎ ‎∴□EGCF是矩形. ‎ ‎{分值}10‎ ‎{章节:[1-18-2-1]矩形}‎ ‎{难度:4-较高难度}‎ ‎{类别:发现探究}‎ ‎{考点:平行四边形边的性质}‎ ‎{考点:全等三角形的判定SAS}‎ ‎{考点:一组对边平行且相等的四边形是平行四边形}‎ ‎{考点:矩形的判定}‎ ‎{题目}22．（2019年青岛）某商店购进一批成本为每件 30 元的商品，经调查发现，该商品每天的销售量 y（件）与销售单价 x（元）之间满足一次函数关系，其图象如图所示.‎ ‎（1）求该商品每天的销售量 y 与销售单价 x 之间的函数关系式；‎ ‎（2）若商店按单价不低于成本价，且不高于 50 元销售，则销售单价定为多少，才能使 销售该商品每天获得的利润 w（元）最大？最大利润是多少？‎ ‎（3）若商店要使销售该商品每天获得的利润不低于 800 元，则每天的销售量最少应为多 少件？‎ ‎{解析}本题是一道综合考查一次函数和二次函数的实际应用题，理解各个数量之间的关系是解题的关键．（1）利用待定系数法求y与x之间的函数关系式；（2）由题意，得30≤x≤50，根据“每天获得的利润＝每件利润×每天销售量”求出w与x的函数关系，结合x的取值范围求w的最大值；（3）由题意，得w≥800.由w＝800时x的值得到w≥800时x的取值范围，再结合y与x之间的函数关系式确定y的最小值.‎ ‎{答案}解： （1）设y与x之间的函数关系式为y＝kx＋b， 将（30,100）（45,70）代入上式，得，解得∴y与x之间的函数关系式为y＝-2x＋160. ‎ ‎（2）根据题意，得w＝y（x-30）＝（-2x＋160）（x-30）＝-2x2＋220x-4800＝-2（x-55）2＋1250.‎ ‎∴当x≤55时，w随x的增大而增大.‎ ‎∵30≤x≤50，∴当x＝50时，y最大值＝1200.‎ 答：销售单价定为50元/件时，才能使销售该商品每天获得的利润 w（元）最大，最大利润是1200元. ‎ ‎（3）将w＝800代入w＝-2（x-55）2＋1250，得x1＝40,x2＝70.‎ ‎∴当40≤x≤70时，w≥800.‎ 对于y＝-2x＋160， y随x的增大而减小，故当x＝70时，y最小值＝20.‎ 答：若商店要使销售该商品每天获得的利润不低于 800 元，则每天的销售量最少应为20件. ‎ ‎{分值}10‎ ‎{章节:[1-22-3]实际问题与二次函数}‎ ‎{难度:4-较高难度}‎ ‎{类别:常考题}‎ ‎{考点:一次函数的图象}‎ ‎{考点:商品利润问题}‎ ‎{考点:待定系数法求一次函数的解析式}‎ ‎{题目}23．（2019年青岛）问题提出：‎ 如图，图①是一张由三个边长为 1 的小正方形组成的“L”形纸片，图②是一张 a ´b 的 方格纸（a´ b的方格纸指边长分别为 a，b 的矩形，被分成 a ´b个边长为 1 的小正方形，其中 a≥2 ， b≥2，且 a，b 为正整数） ．把图①放置在图②中，使它恰好盖住图②中的三个小正方形，共有多少种不同的放置方法？‎ ‎ ‎ 问题探究：‎ 为探究规律，我们采用一般问题特殊化的策略，先从最简单的情形入手，再逐次递进，‎ 最后得出一般性的结论．‎ 探究一：‎ 把图①放置在 2 ´2的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的 放置方法？‎ 如图③，对于 2´2的方格纸，要用图①盖住其中的三个小正方形，显然有 4 种不同的放 置方法．‎ 探究二：‎ 把图①放置在 3´2的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的 放置方法？‎ 如图④，在 3´2的方格纸中，共可以找到 2 个位置不同的 2 2 ´ 方格，依据探究一的结论 可知，把图①放置在 3´2 的方格纸中，使它恰好盖住其中的三个小正方形，共有 2 ´ 4＝8种 不同的放置方法．‎ 探究三：‎ 把图①放置在 a ´ 2 的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的 放置方法？‎ 如图⑤， 在 a ´ 2 的方格纸中，共可以找到_________个位置不同的 2´2方格，依据探究 一的结论可知，把图①放置在 a ´ 2 的方格纸中，使它恰好盖住其中的三个小正方形，共有 ‎_________种不同的放置方法．‎ ‎ ‎ 探究四：‎ 把图①放置在 a ´ 3 的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的 放置方法？‎ 如图⑥，在 a ´ 3 的方格纸中，共可以找到_________个位置不同的 2´ 2方格，依据探究 一的结论可知，把图①放置在 a ´ 3 的方格纸中，使它恰好盖住其中的三个小正方形，共有 ‎_________种不同的放置方法．‎ ‎……‎ 问题解决：‎ 把图①放置在 a ´ b的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的 放置方法？（仿照前面的探究方法，写出解答过程，不需画图．）‎ 问题拓展：‎ 如图，图⑦是一个由 4 个棱长为 1 的小立方体构成的几何体，图⑧是一个长、宽、高分 别为 a，b ，c （a≥2 ， b≥2 ， c≥2 ，且 a，b，c 是正整数）的长方体，被分成了 a ´b ´c ‎ 个棱长为 1 的小立方体．在图⑧的不同位置共可以找到_________个图⑦这样的几何体．‎ ‎{解析}本题是一道规律探究题，理解探究一、二是正确解答后面问题的前提．探究三：如图⑤，在 a×2 的方格纸中，共可以找到（a－1）个位置不同的 2×2方格；依据探究一的结论可知图①在每个2×2的方格中有4种不同的放置方法，所以把图①放置在 a×2 的方格纸中，共有（a－1）×4种不同的放置方法. ‎ 探究四：在 a×3 的方格纸中，共可以找到（a－1）×（3－1）个位置不同的 2×2方格；依据探究一的结论可知图①在每个2×2的方格中有4种不同的放置方法，所以把图①放置在 a×3的方格纸中，共有（a－1）×（3－1）×4种不同的放置方法. ‎ 问题解决：在 a×b的方格纸中，共可以找到（a－1）×（b－1）个位置不同的 2×2方格；依据探究一的结论可知图①在每个2×2的方格中有4种不同的放置方法，所以把图①放置在 a×b的方格纸中，共有（a－1）×（b－1）×4种不同的放置方法.‎ 问题拓展：在 a×b×c的几何体中，共可以找到（a－1）×（b－1）×（c－1）个位置不同的2×2×2的正方体；而图⑦在每个2×2×2的正方体中有8种不同的放置方法，所以把图⑦放置在 a×b×c的几何体中，共有（a－1）×（b－1）×（c－1）×8种不同的放置方法.‎ ‎{答案}解： 探究三：a－1 4a－4； ‎ 探究四：2（a－1）,8a－8； ‎ 问题解决：4（a－1）（b－1）； ‎ 问题拓展：8（a－1）（b－1）（c－1）. ‎ ‎{分值}10‎ ‎{章节:[1-29-2]三视图}‎ ‎{难度:5-高难度}‎ ‎{类别:思想方法}‎ ‎{类别:高度原创}‎ ‎{类别:发现探究}‎ ‎{考点:规律－图形变化类}‎ ‎{题目}24．（2019年青岛）已知：如图，在四边形 ABCD 中， AB∥CD， ÐACB＝90°， AB＝10cm， BC＝8cm， OD 垂 直平分 A C．点 P 从点 B 出发，沿 BA 方向匀速运动，速度为 1cm/s；同时，点 Q 从点 D 出发，沿 DC 方向匀速运动，速度为 1cm/s；当一个点停止运动，另一个点也停止运动．过点 P作 PE⊥AB，交 BC 于点 E，过点 Q 作 QF∥AC，分别交 AD， OD 于点 F， G．连接 OP，‎ EG．设运动时间为 t ( s )（0＜t＜5） ，解答下列问题：‎ ‎（1）当 t 为何值时，点 E 在 ÐBAC 的平分线上？‎ ‎（2）设四边形 PEGO 的面积为 S(cm2) ，求 S 与 t 的函数关系式；‎ ‎（3）在运动过程中，是否存在某一时刻 t ，使四边形 PEGO 的面积最大？若存在，求出 t 的值；若不存在，请说明理由；‎ ‎（4）连接 OE， OQ，在运动过程中，是否存在某一时刻 t ，使 OE⊥OQ？若存在，求出 t 的值；若不存在，请说明理由．‎ ‎{解析}本题是一道与动点有关的压轴题，综合考查了相似三角形的判定和性质、直角三角形的性质、角平分线的性质、二次函数等知识，难度较大．（1）当点E在∠BAC的平分线上时，有PE＝EC.故将PE和EC用含t的代数式表示出来即可列方程求出t的值.（2）四边形PEGO是一般四边形，故不能直接求其面积，根据S四边形PEGO＝ S△ABC＋ S△OCD―S△AOP―S△BPE―S梯形GDCE求解即可.（3）利用（2）中所求二次函数关系式求解.（4）假设存在某一时刻t，使得OE⊥OQ.此时有△OCE∽△△OQG,进而根据相似三角形对应边成比例列出关于t的方程求解.‎ ‎{答案}解：（1）由题意，得BP＝DQ＝t.‎ 在△ABC中，∵∠ACB＝90°，AB＝10，BC＝8， ‎ ‎∴AC＝＝6.‎ ‎∵PE⊥AB，∴∠BPE＝90°，∴∠BPE＝∠ACB.‎ 又∵∠PBE＝∠ABC，∴△EBP∽△ABC.‎ ‎∴，即，‎ ‎∴PE＝，BE＝.∴EC＝8-.‎ 当点E在∠BAC的平分线上时，PE＝EC.‎ ‎∴＝8-，解得t＝4. ‎ ‎（2）如图，过点P作PH⊥AC于H，∴∠AHP＝∠ACB＝90°.‎ ‎∴PH∥BC，∴△APH∽△ABC.‎ ‎∴，即 ‎∴PH＝ .‎ ‎∵OD垂直平分AC，AC＝6，∴OA＝OC＝3，∠AOD＝∠COD＝90°.‎ ‎∴S△AOP＝×AO×PH＝×3×（）＝12.‎ ‎∵AB∥CD，∴∠ACD＝∠BAC.‎ 又∵∠COD＝∠ACB，∴△COD∽△ACB.‎ ‎∴，即，∴CD＝5,OD＝4.‎ ‎∵QF∥AC，∴△DGQ∽△DOC，∴，即，∴GD＝,GQ＝.‎ ‎∴S梯形GDCE＝（GD＋EC）×OC＝（＋8-）×3＝12-.‎ 又∵S△ABC＝×BC×AC＝×8×6＝24，S△OCD＝×OC×OD＝×3×4＝6,‎ S△BPE＝×BP×PE＝×t×＝,‎ ‎∴S四边形PEGO＝ S△ABC＋ S△OCD―S△AOP―S△BPE―S梯形GDCE ‎＝24＋6-（12）--（12-）‎ ‎＝（0＜t＜5）. ‎ ‎（3）对于S四边形PEGO＝，‎ ‎∵＜0，∴当t＝－时，S四边形PEGO最大. ‎ ‎（4）假设存在某一时刻t，使得OE⊥OQ.‎ 此时∠EOQ＝∠DOC＝90°，∴∠EOC＝∠DOQ.‎ ‎∵∠OCE＝∠OGQ＝90°，∴△OCE∽△△OQG,‎ ‎∴，即，‎ 即t2-13.2 t＋32＝0，解得t1＝3.2,t2＝10（舍去）.‎ 即当t＝3.2时，OE⊥OQ. ‎ ‎ ‎ ‎{分值}12‎ ‎{章节:[1-27-1-2]相似三角形的性质}‎ ‎{难度:5-高难度}‎ ‎{类别:发现探究}‎ ‎{考点:几何图形最大面积问题}‎ ‎{考点:角平分线的性质}‎ ‎{考点:勾股定理}‎ ‎{考点:相似三角形的判定（两角相等）}‎ ‎{考点:相似三角形的性质}‎