九年级上册青岛版数学课件1-3相似三角形的性质 56页

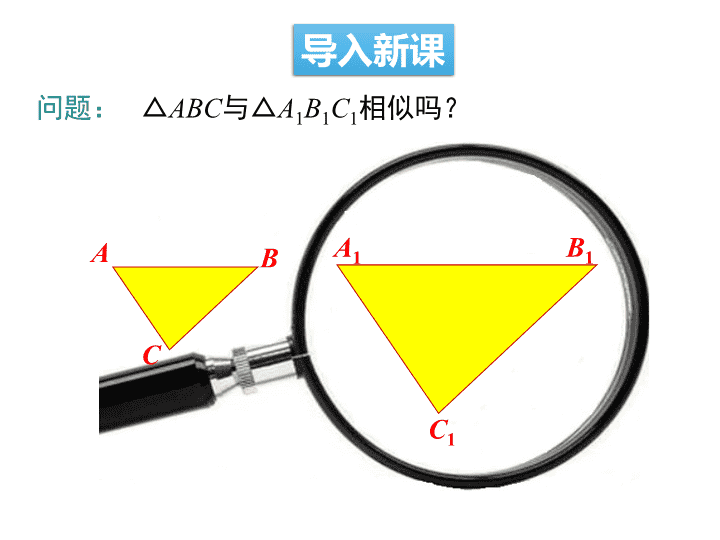
1.3相似三角形的性质 1.明确相似三角形中对应线段与相似比的关系. （重点） 2.能熟练运用相似三角形的性质解决实际问题．（难点） 3.理解并初步掌握相似三角形周长的比等于相似比，面积 的比等于相似比的平方.（重点） 4.掌握相似三角形的周长比、面积比在实际中的应用.（难 点） 学习目标 A C B A1 C1 B1 问题： △ABC与△A1B1C1相似吗？ 导入新课 A C B A1 C1 B1 相似三角形对应角相等、对应边成比例. △ABC∽ △A1B1C1 思考：三角形中，除了角度和边长外，还有哪些 几何量？ 高、角平分线、中线的长度，周长、面积等 高 角平分线 中线 量一量，猜一猜 D1A1 C1 B1 ∟A C BD ∟ ΔABC ∽ ΔA1B1C1, ,CD和C1D1分别是它们 的高, 你知道 等于多少吗？ 1 1 1 2 BC B C  1 1 CD C D 如图，△ABC ∽△A′B′C′，相似比为k，它们 对应高的比各是多少？ A B C A' B' C' 合作探究 相似三角形对应高的比等于相似比知识点 讲授新课 ∵△ABC ∽△A′B′C′， ∴∠B＝∠B' ， 解：如图，分别作出 △ABC 和 △A' B' C' 的高 AD 和 A' D' ． 则∠ADB =∠A' D' B'=90°. ∴△ABD ∽△A' B' D' . A B C A' B' C'D' D     A D A B k.AD AB  由此得到： 相似三角形对应高的比等于相似比． 　　类似的，我们可以得到其余两组对应边上的 高的比也等于相似比． 归纳总结 1. ΔABC∽ ΔA1B1C1 ，BD和B1D1是它们的中线， 已知 ,B1D1 =4cm，则BD= cm.6 2.ΔABC∽ ΔA1B1C1, AD和A1D1是对应角平分 线，已知AD=8cm， A1D1=3cm ,则 ΔABC与 ΔA1B1C1的对应高之比为 .8:3 练一练 1 1 3 2 AC AC  3.如图，电灯P在横杆AB的正上方，AB在灯光下的影 子为CD，AB∥CD，AB=2 m，CD=4 m，点P到CD的 距离是3 m，则P到AB的距离是 m. P A D B C 2 4 1.5 例：如图，AD是ΔABC的高，点P，Q在BC边上， 点R在AC边上，点S在AB边上，BC=60 cm，AD= 40 cm，四边形PQRS是正方形. (1)AE是Δ ASR的高吗？为什么？ (2) ΔASR与ΔABC相似吗？为什么？ (3)求正方形PQRS的边长. S R QP E D CB A 典例精析 （1）AE是ΔASR的高吗？为什么？ 解： AE是ΔASR的高. 理由： ∵AD是ΔABC的高, ∴ ∠ADC=90°. ∵四边形PQRS是正方形, ∴SR∥BC. ∴∠AER=∠ADC=90°. ∴ AE是ΔASR的高. S R QP E D CB A （2） ΔASR与ΔABC相似吗？为什么？ 解： ΔASR与ΔABC相似. 理由: ∵ SR∥BC, ∴ ∠ASR=∠B, ∠ARS=∠C. ∴ ΔASR与ΔABC相似. S R QP E D CB A （3）求正方形PQRS的边长. 是方程思 想哦！ 解：∵ ΔASR ∽ ΔABC, AE,AD分别是ΔASR 和ΔABC 对应边上的高, ∴ . 设正方形PQRS的边长为 x cm, 则SR=DE=x cm,AE=(40-x)cm. ∴ 解得x=24. ∴正方形PQRS的边长为24 cm. BC SR AD AE  6040 40 xx   S R QP E D CB A 变式： 如图，AD是ΔABC的高，点P，Q在BC边上，点R在 AC边上，点S在AB边上，BC=5cm，AD=10cm，若 矩形PQRS的长是宽的2倍，你能求出这个矩形的面 积吗？ S R QP E D CB A 如图，AD是ΔABC的高，BC=5cm，AD=10cm. 设SP=x cm，则SR=2x cm. 得到： 所以 x=2, 2x=4. S矩形PQRS= 2×4=8 cm2 .   10 x 2x 10 5 S R QP E D CB A分析： 情况一：SR=2SP. 设SR=x cm，则SP=2x cm. 得到： . 所以 x=2.5, 2x=5. S矩形PQRS=2.5×5=12.5 cm2 .   10 2x x 10 5 原来是分类 思想呀！ S R QP E D CB A 分析： 情况二：SP=2SR. 如图，AD是ΔABC的高，BC=5 cm，AD=10 cm. 相似三角形对应角平分线的比、对应中线的比都等 于相似比 问题：把上图中的高改为中线、角平分线，那么它们 对应中线的比，对应角平分线的比等于多少？ 图中△ABC和△A′B′C′相似，AD,A′D′分别为 对应边上的中线，BE,B′E′分别为对应角的角平分 线，那么它们之间有什么关系呢？ A B CD E A' B' D' C' E' 知识点 已知：△ABC∽△A′B′C′，相似比为k， 求证： 证明：∵ △ABC∽△A′B′C′. ∴ ∠B′= ∠B, ． 又AD,AD′分别为对应边的中线, ∴ △ABD∽△A′B′D′. ' ' ' ' ' ' .AB BC CA k A B B C C A    .AD k A'D'  .k A'D' AD  ' ' ' ' AB BC A B B C  ' ' ' ' AB BD A B B D ∴ ， A' B' D' C' E' A B CD E 验证猜想1 由此得到： 相似三角形对应的中线的比也等于相 似比． 同学们可以试着自己用同样的方 法求证三角形对应边上的角平分 中线的比等于相似比． 归纳总结 已知：△ABC∽△A′B′C′，相似比为k，即 求证： 证明：∵ △ABC∽△A′B′C′， ∴ ∠B′= ∠B, ∠B′A′C′= ∠BAC． 又AD,AD′分别为对应角的平分线， ∴ △ABD∽△A′B′D′. ' ' ' ' ' ' .AB BC CA k A B B C C A    A' B' D' C' E' A B CD E 验证猜想2 相似三角形对应高的比、对应角平分线的比、 对应中线的比都等于相似比，即相似三角形 对应线段的比等于相似比． 归纳总结 例：两个相似三角形的两条对应边的长分别是6cm 和8cm，如果它们对应的两条角平分线的和为42cm， 那么这两条角平分线的长分别是多少？ 解：设较短的角平分线长为xcm， 则由相似性质有 . 解得x＝18. 较长的角平分线长为24cm. 故这两条角平分线的长分别为18cm，24cm. 6 , 42 14 x  问题：我们知道，如果两个三角形相似，它们对应 高的比、对应中线的比和对应角平分线的比都等于 相似比.那么它们周长的比之间有什么关系？也等于 相似比吗？面积之比呢？ A B C A1 B1 C1 问题：图中(1)(2)(3)分别是边长为1，2，3的等边 三角形,它们都相似吗？ (1) (2) (3) 1 2 3 (1)与(2)的相似比=______, (1)与(2)的周长比=______， (1)与(3)的相似比=______, (1)与(3)的周长比=______. 1∶ 2 结论： 相似三角形的 周长比等于______．相似比 （都相似） 1∶ 3 1∶ 2 1∶ 3 有什么规律 吗？ 相似三角形周长比等于相似比知识点 讲授新课 证明：设△ABC∽△A1B1C1，相似比为k， ,k AC CA CB BC BA AB  111111 1 1 1 1 1 1, , ,AB kA B BC kB C CA kC A    .k ACCBBA AkCCkBBkA ACCBBA CABCAB       111111 111111 111111 有 求证：相似三角形的周长比等于相似比. A B C A1 B1 C1 想一想：怎么证明这一结论呢？ 相似三角形周长的比等于相似比. 归纳总结 (1)与(2)的相似比=______, (1)与(2)的面积比=______ (1)与(3)的相似比=______, (1)与(3)的面积比=______ 1 2 3 1∶ 2 （1） （2） （3） 1∶ 4 1∶ 3 1∶ 9 问题：图中(1)(2)(3)分别是边长为1，2，3的等边 三角形,回答以下问题： 结论： 相似三角形的面 积比等于____________．相似比的平方 相似三角形面积的比等于相似比的平方知识点 证明：设△ABC∽△A′B′C′，相似比为k, 如图，分别作出△ABC和 △A′B′C′的高AD和A′D′. ∵△ABC和△A′B′C′都是直角三角 形，并且∠B=∠B′， ∴△ABD∽△A′B′D′. .     BA AB DA AD A B C A′ B′ C′ D D′ 想一想：怎么证明这一结论呢？ ∵△ABC∽△A′B′C′. .AD k A D     2 1 2 .1 2 ABC A B C BC ADS BC AD k k k S B C A DB C A D △ △                    .AB BC A B B C       相似三角形面积的比等于相似比的平方. 归纳总结 1.已知ΔABC与ΔA′B′C′的相似比为2：3，则对 应边上中线之比 ，面积之比为 . 2. 如果两个相似三角形的面积之比为1:9， 周长的比为______ . 1:3 2:3 4:9 练一练 解：根据题意，可知EG∥AB. ∴∠GEC=∠B,∠EGC=∠A. ∴△GEC∽△ABC. 2 2 2 GEC ABC S EC EC S BC BC △ △        2 2 1 2 2 EC   2 2. 2.EC EC    2 2.BE BC EC     2 2. 解：在 △ABC 和 △DEF 中， ∵ AB=2DE，AC=2DF， 又 ∵∠D=∠A， ∴ △DEF ∽ △ABC ，相似比为 1 : 2. A B C D E F 1 . 2 DE DF AB AC  ∴ 例 如图，在 △ABC 和 △DEF 中，AB = 2 DE ，AC = 2 DF，∠A = ∠D. 若 △ABC 的边 BC 上的高为 6， 面积为 ，求 △DEF 的边 EF 上的高和面积.12 5 A B C D E F ∵△ABC 的边 BC 上的高为 6，面积为 ，12 5 ∴△DEF 的边 EF 上的高为 ×6 = 3， 1 2 面积为 21 12 5 3 5. 2        如果两个相似三角形的面积之比为 2 : 7，较 大三角形一边上的高为 7，则较小三角形对应边上 的高为______. 14 练一练 5 3  AB AD AC AE ∴ △ADE ∽△ABC. ∵ 它们的相似比为 3 : 5， ∴ 面积比为 9 : 25. B C A D E 解：∵ ∠BAC = ∠DAE，且 3 5 AE AD AC AB   ， 又∵ △ABC 的面积为 100 cm2， ∴ △ADE 的面积为 36 cm2 . ∴ 四边形 BCDE 的面积为100－36 = 64 (cm2). B C A D E 如图，△ABC 中，点 D、E、F 分别在 AB，AC， BC 上，且 DE∥BC，EF∥AB. 当 D 点为 AB 中点时， 求 S四边形BFED : S△ABC 的值. A B C D F E 练一练 解：∵ DE∥BC，D 为 AB 中点， ∴ △ADE ∽ △ABC ， 相似比为 1 : 2， 面积比为 1 : 4. 1 2 AE AD . AC AB  ∴ A B C D F E 又∵ EF∥AB， ∴ △EFC ∽ △ABC ，相似比为 1 : 2， 面积比为 1 : 4. 设 S△ABC = 4，则 S△ADE = 1，S△EFC = 1， S四边形BFED = S△ABC－S△ADE－S△EFC = 4－1－1 = 2， ∴ S四边形BFED : S△ABC = 2 : 4 = 1 . 2 3．两个相似三角形对应中线的比为 ， 则对应高的比为______ . 2.相似三角形对应边的比为2∶ 3,那么对应角的 角平分线的比为______.2∶ 3 1．两个相似三角形的相似比为 , 则对应高 的比为_________, 则对应中线的比为_________. 1 2 2 1 2 1 4 1 4 1 随堂练习 解：∵ △ABC∽△DEF， 　 解得,EH＝3.2(cm). 答：EH的长为3.2cm. A G B C D E F H 4.已知△ABC∽△DEF，BG，EH分△ABC和△DEF 的角平分线，BC=6cm,EF=4cm,BG=4.8cm.求EH的长. BG BC EH EF   4.8 6 , 4EH   5.如图，AD是△ABC的高，AD=h, 点R在AC边上， 点S在AB边上，SR⊥AD，垂足为E.当 时， 求DE的长.如果 呢？ 　 ∴△ASR∽△ABC (两角分别相等的两个三角形相似). 解：∵SR⊥AD，BC⊥AD， B A E R C 1 = 2 SR BC 1 = 3 SR BC D S ∴SR∥BC. ∴∠ASR=∠B,∠ARS=∠C. AE SR AD BC   (相似三角形对应高的比等于相似比)， 当 时，得 解得 B A E R CD S .AD DE SR AD BC    当 时，得 解得 1 = 2 SR BC 1 . 2 h DE AD   1 . 2 DE h 1 = 3 SR BC 1 . 3 h DE AD   2 . 3 DE h 选做题： 6. 一块直角三角形木板的一条直角边AB长为1.5m， 面积为1.5m2,要把它加工成一个面积尽可能大的正方形 桌面，甲乙两位同学的加工方法如图（1）、（2)所示， 请你用学过的知识说明哪位同学的加工方法更好.（加 工损耗忽略不计，计算结果中的分数可保留） F AB C D E （1） FG B A C ED （2） 相信自己是最 棒的！ S R QP E D CB A 7.AD是ΔABC的高，BC=60cm，AD=40cm，求图中 小正方形的边长. A CB D (6) A CB D (5) D CB A (4) A CB D (3) D CB A (1) A CB D (2) 8. 判断： (1) 一个三角形的各边长扩大为原来的 5 倍，这个 三角形的周长也扩大为原来的 5 倍 ( ) (2) 一个四边形的各边长扩大为原来的 9 倍，这个 四边形的面积也扩大为原来的 9 倍 ( ) √ × 10. 连接三角形两边中点的线段把三角形截成的一 个小三角形与原三角形的周长比等于______，面积 比等于_____. 1 : 2 1 : 4 9. 在 △ABC 和 △DEF 中，AB＝2 DE，AC＝2 DF， ∠A＝∠D，AP，DQ 是中线，若 AP＝2，则 DQ 的值为 ( ) A．2 B．4 C．1 D. C 2 1 11. 两个相似三角形对应的中线长分别是 6 cm 和 18 cm， 若较大三角形的周长是 42 cm，面积是 12 cm2，则较小 三角形的周长____cm，面积为____cm2.14 4 3 12. 如图，这是圆桌正上方的灯泡 (点A) 发出的光线 照 射桌面形成阴影的示意图，已知桌面的直径为 1.2 米，桌面距离地面为 1 米，若灯泡距离地面 3 米， 则地面上阴影部分的面积约为多少 (结果保留两位 小数)？ A DE F CB H 解：∵ FH = 1 米，AH = 3 米， 桌面的直径为 1.2 米， ∴ AF = AH－FH = 2 (米)， DF = 1.2÷2 = 0.6 (米). ∵DF∥CH， ∴△ADF ∽△ACH， A DE F CB H DF AF CH AH  ，∴ 即 0 6 2 3 . CH  ， 解得 CH = 0.9米. ∴ 阴影部分的面积为： 2 20.9 2.54CH    (平方米). 答：地面上阴影部分的面积为 2.54 平方米. 13. △ABC 中，DE∥BC，EF∥AB，已知 △ADE 和 △EFC 的面积分别为 4 和 9，求 △ABC 的面积.A B C D F E 解：∵ DE∥BC，EF∥AB， ∴ △ADE ∽△ABC， ∠ADE =∠EFC，∠A =∠CEF， ∴△ADE ∽△EFC. 又∵S△ADE : S△EFC = 4 : 9， ∴ AE : EC=2:3， 则 AE : AC =2 : 5， ∴ S△ADE : S△ABC = 4 : 25，∴ S△ABC = 25. 14. 如图，△ABC 中，DE∥BC，DE 分别交 AB，AC 于 点 D，E，S△ADE＝2 S△DCE，求 S△ADE ∶ S△ABC. 解：过点 D 作 AC 的垂线，交点为 F，则 1 2 21 2 ADE DCE AE DFS AE S ECEC DF        △ △ ， 2 3 AE . AC ∴ 又∵ DE∥BC， ∴ △ADE ∽△ABC. A B C D E 2 22 4 3 9 ADE ABC S AE S AC              △ △ ，∴ 即 S△ADE : S△ABC ＝4 : 9. A B C D E 相似三 角形的 性质 相似三角形对应高的 比等于相似比 相似三角形对应角平 分线的比等于相似比 相似三角形对应中线 的比等于相似比 课堂小结 相似三角形 的性质 相似三角形周长之比 等于相似比 相似三角形面积之比 等于相似比的平方