2020-2021学年华师大版九年级上册第23章、第24章测试题及答案（各一套） 18页

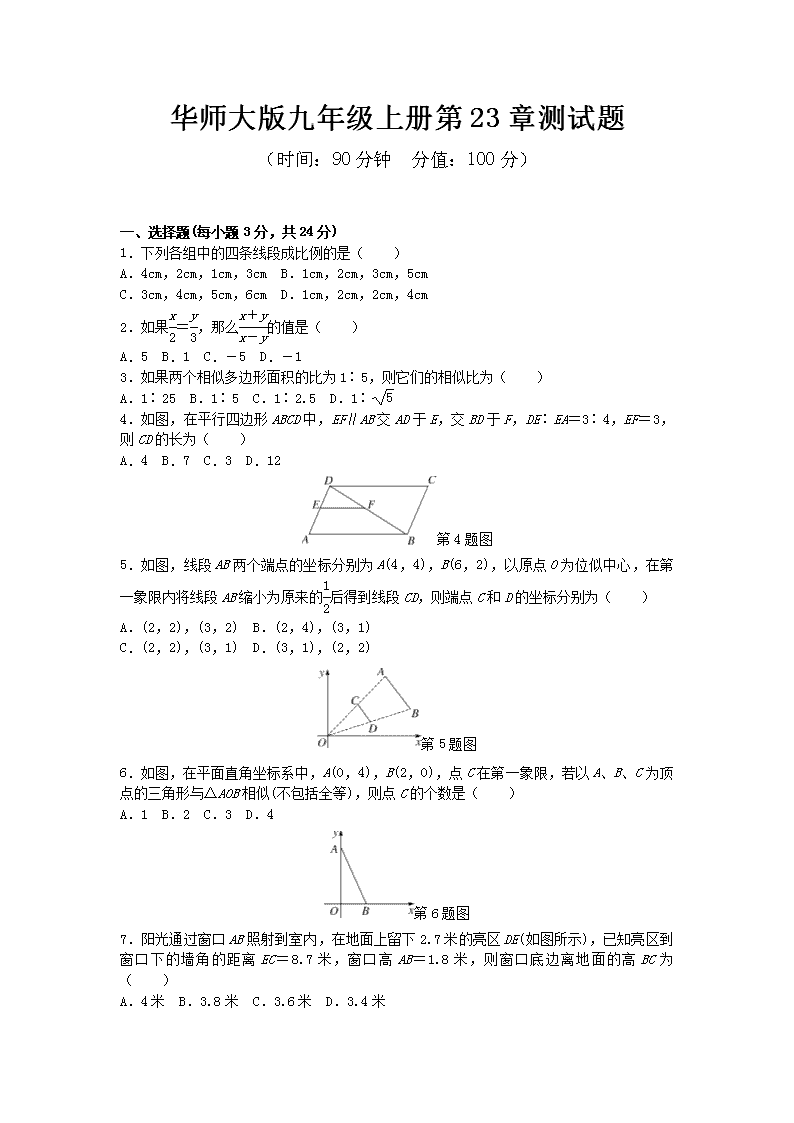
华师大版九年级上册第23章测试题 ‎（时间：90分钟　分值：100分）‎ 一、选择题(每小题3分，共24分)‎ ‎1．下列各组中的四条线段成比例的是（ ）‎ A．4cm，2cm，1cm，3cm B．1cm，2cm，3cm，5cm C．3cm，4cm，5cm，6cm D．1cm，2cm，2cm，4cm ‎2．如果＝，那么的值是（ ）‎ A．5 B．1 C．－5 D．－1‎ ‎3．如果两个相似多边形面积的比为1∶5，则它们的相似比为（ ）‎ A．1∶25 B．1∶5 C．1∶2.5 D．1∶ ‎4．如图，在平行四边形ABCD中，EF∥AB交AD于E，交BD于F，DE∶EA＝3∶4，EF＝3，则CD的长为（ ）‎ A．4 B．7 C．3 D．12‎ 第4题图 ‎5．如图，线段AB两个端点的坐标分别为A(4，4)，B(6，2)，以原点O为位似中心，在第一象限内将线段AB缩小为原来的后得到线段CD，则端点C和D的坐标分别为（ ）‎ A．(2，2)，(3，2) B．(2，4)，(3，1) ‎ C．(2，2)，(3，1) D．(3，1)，(2，2)‎ 第5题图 ‎6．如图，在平面直角坐标系中，A(0，4)，B(2，0)，点C在第一象限，若以A、B、C为顶点的三角形与△AOB相似(不包括全等)，则点C的个数是（ ）‎ A．1 B．2 C．3 D．4‎ 第6题图 ‎7．阳光通过窗口AB照射到室内，在地面上留下2.7米的亮区DE(如图所示)，已知亮区到窗口下的墙角的距离EC＝8.7米，窗口高AB＝1.8米，则窗口底边离地面的高BC为（ ）‎ A．4米 B．3.8米 C．3.6米 D．3.4米 第7题图 ‎8．如图，正方形ABCD的对角线AC与BD相交于点O，∠ACB的平分线分别交AB、BD于M、N两点．若AM＝2，则线段ON的长为（ ）‎ A. B. C．1 D. 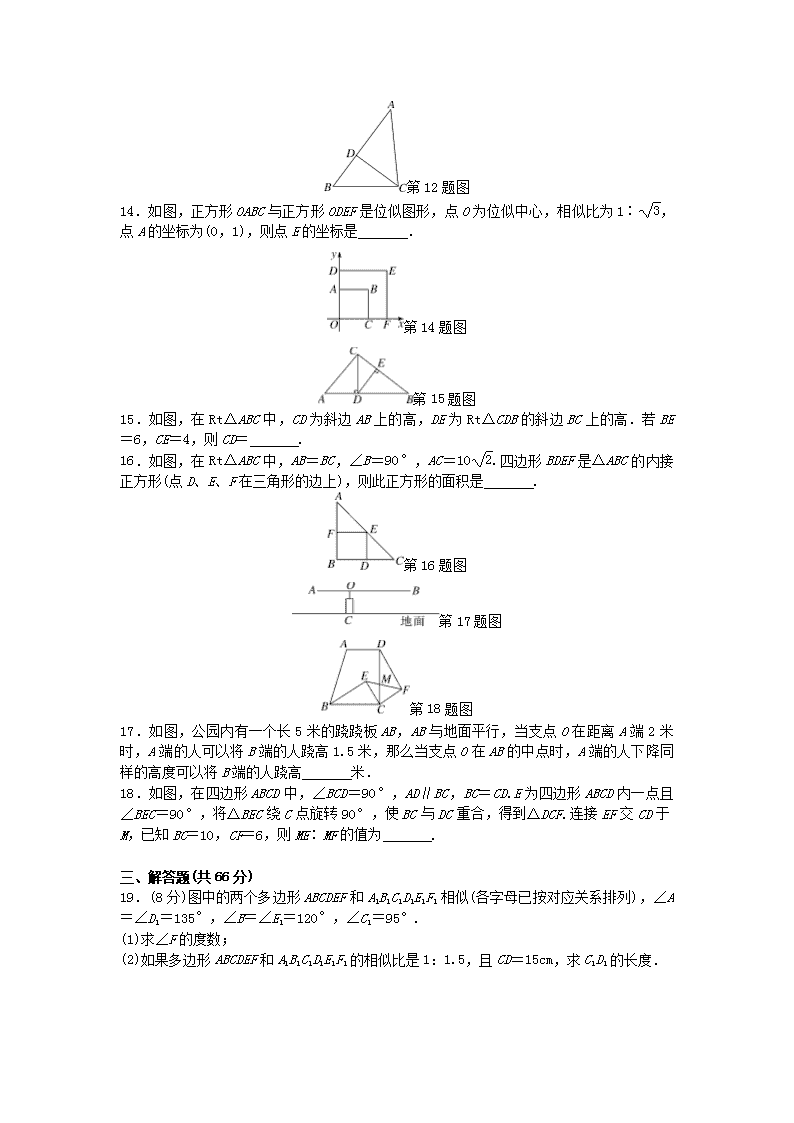第8题图 二、填空题(每小题3分，共30分)‎ ‎9．如图，为估计池塘两岸边A，B两点间的距离，在池塘的一侧选取点O，分别取OA，OB的中点M，N，测得MN＝32m，则A，B两点间的距离是 m.‎ 第9题图 ‎10．如图，是象棋棋盘的一部分，若位于点(1，－2)上，位于点 上，则位于点(－2，1)上．‎ 第10题图 ‎11．如图，在△ABC中，DE∥BC，＝，DE＝6，则BC的长是 .‎ 第11题图 ‎12．如图，在△ABC中，D是AB边上的一点，连接CD，请添加一个适当的条件 ，使△ABC∽△ACD(只填一个即可)．‎ ‎13．在同一坐标系中，图形a是图形b向上平移3个单位长度得到的，如果图形a中的点A的坐标为(4，－2)，则图形b中与点A对应的点A′的坐标为 ．‎ 第12题图 ‎14．如图，正方形OABC与正方形ODEF是位似图形，点O为位似中心，相似比为1∶，点A的坐标为(0，1)，则点E的坐标是 ．‎ 第14题图 第15题图 ‎15．如图，在Rt△ABC中，CD为斜边AB上的高，DE为Rt△CDB的斜边BC上的高．若BE＝6，CE＝4，则CD＝ .‎ ‎16．如图，在Rt△ABC中，AB＝BC，∠B＝90°，AC＝10.四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上)，则此正方形的面积是 .‎ 第16题图 第17题图 第18题图 ‎17．如图，公园内有一个长5米的跷跷板AB，AB与地面平行，当支点O在距离A端2米时，A端的人可以将B端的人跷高1.5米，那么当支点O在AB的中点时，A端的人下降同样的高度可以将B端的人跷高 米．‎ ‎18．如图，在四边形ABCD中，∠BCD＝90°，AD∥BC，BC＝CD.E为四边形ABCD内一点且∠BEC＝90°，将△BEC绕C点旋转90°，使BC与DC重合，得到△DCF.连接EF交CD于M，已知BC＝10，CF＝6，则ME∶MF的值为 .‎ 三、解答题(共66分)‎ ‎19．(8分)图中的两个多边形ABCDEF和A1B1C1D1E1F1相似(各字母已按对应关系排列)，∠A＝∠D1＝135°，∠B＝∠E1＝120°，∠C1＝95°.‎ ‎(1)求∠F的度数；‎ ‎(2)如果多边形ABCDEF和A1B1C1D1E1F1的相似比是1：1.5，且CD＝15cm，求C1D1的长度．‎ ‎20．(6分)如图所示，AD、BE是钝角△ABC的边BC、AC上的高，求证：＝.‎ ‎21．(6分)如图，M、N为山两侧的两个村庄，为了两村交通方便，根据国家的惠民政策，政府决定打一直线涵洞．工程人员为了计算工程量，必须计算M、N两点之间的直线距离，选择测量点A、B、C，点B、C分别在AM、AN上，现测得AM＝1千米、AN＝1.8千米、AB＝54米、BC＝45米、AC＝30米，求M、N两点之间的直线距离．‎ ‎22．(7分)已知：△ABC在平面直角坐标平面内，三个顶点的坐标分别为A(0，3)、B(3，4)、C(2，2)(正方形网格中每个小正方形的边长是一个单位长度)．‎ ‎(1)画出△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是(2，－2)；(2分)‎ ‎(2)以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2∶1，点C2的坐标是(1，0)；‎ ‎(3)△A2B2C2的面积是10平方单位．‎ ‎23．(7分)如图，在△ABC中，AB＝AC＝8，BC＝6，点D为BC上一点，BD＝2.过点D作射线DE交AC于点E，使∠ADE＝∠B.求线段EC的长度．‎ ‎24．(10分)如图，在△ABC中，AB＝AC，点P、D分别是BC、AC边上的点，且∠APD＝∠B.‎ ‎(1)求证：AC·CD＝CP·BP；‎ ‎(2)若AB＝10，BC＝12，当PD∥AB时，求BP的长．‎ ‎25．(10分)如图，在平行四边形ABCD中，对角线AC、BD交于点O.M为AD中点，连接CM交BD于点N，且ON＝1.‎ ‎(1)求BD的长；‎ ‎(2)若△DCN的面积为2，求四边形ABNM的面积．‎ ‎26．(12分)如图，正方形OABC的边OA，OC在坐标轴上，点B的坐标为(－4，4)．点P从点A出发，以每秒1个单位长度的速度沿x轴向点O运动；点Q从点O同时出发，以相同的速度沿x轴的正方向运动，规定点P到达点O时，点Q也停止运动．连接BP，过P点作BP的垂线，与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E，连接PE.设点P运动的时间为t(s)．‎ ‎(1)∠PBD的度数为45°，点D的坐标为(t，t)(用t表示)；‎ ‎(2)当t为何值时，△PBE为等腰三角形？‎ 参考答案：‎ ‎1．D　2.C　3.D　4.B　5.C　6.D　7.A ‎8．C　解析：‎ 作MH⊥AC于H，如图.‎ ‎∵四边形ABCD为正方形，‎ ‎∴∠MAH＝45°，‎ ‎∴△AMH为等腰直角三角形，‎ ‎∴AH＝MH＝AM＝×2＝.‎ ‎∵CM平分∠ACB，∴BM＝MH＝，‎ ‎∴AB＝2＋，‎ ‎∴AC＝AB＝(2＋)×＝2＋2，‎ ‎∴OC＝AC＝＋1，CH＝AC－AH＝2＋2－＝2＋.‎ ‎∵BD⊥AC，∴ON∥MH，‎ ‎∴△CON∽△CHM，‎ ‎∴＝，即＝，‎ ‎∴ON＝1.故选C.‎ ‎9．64　10.(－2，1)　11.18‎ ‎12．∠B＝∠ACD(答案不唯一)　13.(4，－5)‎ ‎14．(，)　15.2　16.25　17.1‎ ‎18．3∶4　解析：由题意知△BCE绕点C顺时转动了90°，‎ ‎∴△BCE≌△DCF，∠ECF＝∠DFC＝90°，‎ ‎∴CD＝BC＝10，DF∥CE，‎ ‎∴∠ECD＝∠CDF.‎ ‎∵∠EMC＝∠DMF，‎ ‎∴△ECM∽△FDM，‎ ‎∴ME：MF＝CE：DF.‎ ‎∵DF＝＝8，‎ ‎∴ME：MF＝CE：DF ＝6：8＝3：4.‎ 19． 解：(1)∵多边形ABCDEF和A1B1C1D1E1F1相似，又∠C和∠C1、∠D和∠D1、∠E和∠E1是对应角，‎ ‎∴∠C＝95°，∠D＝135°，∠E＝120°.‎ 由多边形内角和定理，知∠F＝720°－(135°＋120°＋95°＋135°＋120°)＝115°‎ ‎；(4分)‎ (2) ‎∵多边形ABCDEF和A1B1C1D1E1F1的相似比是1：1.5，且CD＝15cm，‎ ‎∴C1D1＝15×1.5＝22.5(cm)．(8分)‎ 19． 解：∵AD、BE是钝角△BAC的高，‎ ‎∴∠BEC＝∠ADC＝90°.(2分)‎ 又∵∠DCA＝∠ECB，∴△DAC∽△EBC.(5分)‎ ‎∴＝.(6分)‎ 20． 解：在△ABC与△AMN中，∠A＝∠A，＝＝，＝＝，‎ ‎∴＝，即＝，∴△ABC∽△ANM，(3分)‎ ‎∴＝，即＝，∴MN＝1.5千米．(5分)‎ 答：M、N两点之间的直线距离是1.5千米．(6分)‎ ‎22．解：(1)(2，－2)(2分)‎ ‎(2)(1，0)(4分)‎ ‎(3)10(7分)‎ 21． 解：∵AB＝AC，∴∠B＝∠C.(2分)‎ ‎∵∠ADC＝∠B＋∠BAD，∠ADC＝∠ADE＋∠EDC，而∠B＝∠ADE，‎ ‎∴∠BAD＝∠EDC.(5分)∴△ABD∽△DCE.‎ ‎∴＝.∴＝.∴EC＝1.(7分)‎ 22． ‎(1)证明：∵AB＝AC，∴∠B＝∠C.(1分)‎ ‎∵∠APD＝∠B，∴∠APD＝∠B＝∠C.‎ ‎∵∠APC＝∠BAP＋∠B，∠APC＝∠APD＋∠DPC，‎ ‎∴∠BAP＝∠DPC，∴△ABP∽△PCD，(3分)‎ ‎∴＝，∴AB·CD＝CP·BP.‎ ‎∵AB＝AC，∴AC·CD＝CP·BP；(5分)‎ (3) 解：∵PD∥AB，∴∠APD＝∠BAP.‎ ‎∵∠APD＝∠C，∴∠BAP＝∠C.‎ ‎∵∠B＝∠B，‎ ‎∴△BAP∽△BCA，∴＝.(8分)‎ ‎∵AB＝10，BC＝12，‎ ‎∴＝，∴BP＝.(10分)‎ 23． 解：(1)∵四边形ABCD是平行四边形，‎ ‎∴AD∥BC，AD＝BC，OB＝OD，‎ ‎∴∠DMN＝∠BCN，∠MDN＝∠NBC，‎ ‎∴△MND∽△CNB，∴＝.(2分)‎ ‎∵M为AD中点，‎ ‎∴MD＝AD＝BC，即＝，‎ ‎∴＝，即BN＝2DN.‎ 设OB＝OD＝x，则有BD＝2x，BN＝OB＋ON＝x＋1，DN＝x－1，‎ ‎∴x＋1＝2(x－1)，解得x＝3，‎ ‎∴BD＝2x＝6；(5分)‎ (2) ‎∵△MND∽△CNB，且相似比为1∶2，‎ (3) ‎∴MN∶CN＝DN∶BN＝1∶2，‎ (4) ‎∴S△MND＝S△CND＝1，S△BNC＝2S△CND＝4.‎ (5) ‎∴S△ABD＝S△BCD＝S△BCN＋S△CND＝4＋2＝6，(8分)‎ (6) ‎∴S四边形ABNM＝S△ABD－S△MND＝6－1＝5.(10分)‎ ‎26．解：(1)45°　(t，t)(4分)‎ ‎(2)由题意，可得AP＝OQ＝1×t＝t，‎ ‎∴AO＝PQ.(5分)‎ ‎∵四边形OABC是正方形，‎ ‎∴AO＝AB，∴AB＝PQ.‎ ‎∵DP⊥BP，∴∠BPD＝90°.‎ ‎∴∠BPA＝90°－∠DPQ＝∠PDQ.‎ 又∵∠BAP＝∠PQD＝90°，‎ ‎∴△PAB≌△DQP.(7分)‎ ‎∴AP＝DQ＝t，PB＝PD.‎ 显然PB≠PE，分两种情况：‎ 若EB＝EP，则∠EPB＝∠EBP＝45°，此时点P与O点重合，t＝4；‎ 若BE＝BP，则△PAB≌△ECB.∴CE＝PA＝t.(9分)‎ 过D点作DF⊥OC于点F，易知四边形OQDF为正方形，‎ 则DF＝OF＝t，EF＝4－2t.‎ ‎∵DF∥BC，∴△BCE∽△DFE，‎ ‎∴＝，∴＝.解得t＝－4±4(负根舍去)．‎ ‎∴t＝4－4.(11分)‎ 综上，当t＝4－4或4时，△PBE为等腰三角形．(12分)‎ 华师大版九年级上册第24章测试题 ‎（时间：90分钟　分值：100分）‎ 一、选择题(每小题3分，共24分)‎ ‎1．cos60°的值等于（ ）‎ A. B. C. D. ‎2．已知sinA＝，则锐角A的度数是（ ）‎ A．30° B．45° C．60° D．75°‎ ‎3．在Rt△ABC中，∠C＝90°，AC＝12，BC＝5，则sinA的值为（ ）‎ A. B. C. D. ‎4．在等腰△ABC中，AB＝AC＝10cm，BC＝12cm，则cos的值是（ ）‎ A. B. C. D. ‎5．如图，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则∠ABC的正切值是（ ）‎ A．2 B. C. D. 第5题图 ‎6．如图，一河坝的横断面为等腰梯形ABCD，坝顶宽10米，坝高12米，斜坡AB的坡度i＝1∶1.5，则坝底AD的长度为（ ）‎ A．26米 B．28米 C．30米 D．46米 ‎ 第6题图 ‎7．如图，为了测得电视塔的高度AB，在D处用高为1m的测角仪CD，测得电视塔顶端A的仰角为30°，再向电视塔方向前进100m到达F处，又测得电视塔顶端A的仰角为60°，则这个电视塔的高度AB为（ ）‎ A．50m B．51m C．(50＋1)m D．101m ‎ 第7题图 ‎8．如图，在Rt△BAD中，延长斜边BD到点C，使DC＝BD，连接AC，若tanB＝，则tan∠CAD的值为（ ）‎ A. B. C. D. 二、填空题(每小题3分，共30分)‎ ‎9．在△ABC中，∠C＝90°，AB＝5，AC＝3，则cosA＝ .‎ ‎10．在△ABC中，若cosB＝，tanA＝，且∠A，∠B为锐角，则△ABC是 三角形．‎ ‎11．如图，在△ABC中，∠C＝90°，∠B＝30°，AD平分∠CAB，交BC于点D，若CD＝1，则BD＝ .‎ 第11题图 第14题图 ‎12．在Rt△ABC中，∠ACB＝90°，CD是斜边AB上的中线，CD＝4，AC＝6，则sinB的值是 ．‎ ‎13．在△ABC中，已知∠C＝90°，sinA＋sinB＝，则sinA－sinB＝ .‎ ‎14．如图，小明用长为3m的竹竿CD做测量工具，测量学校旗杆AB的高度，移动竹竿，使竹竿与旗杆的距离DB＝12m，则旗杆AB的高为 m.‎ ‎15．长为4m的梯子搭在墙上与地面成45°，作业时调整成60°(如图所示)，则梯子的顶端沿墙面升高了 m.‎ 第15题图 ‎16．观光塔是潍坊市区的标志性建筑，为测量其高度，如图，一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°，然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m，根据以上观测数据可求观光塔的高CD是 m.‎ 第16题图 ‎17．如图，将矩形ABCD沿AE折叠，点D恰好落在BC边上的点F处，如果AB：AD＝2：3，那么tan∠EFC值是 ．‎ 第17题图 ‎18．如图，小华站在河岸上的G点，看见河里有一小船沿垂直于岸边的方向划过来．此时，测得小船C的俯角是∠FDC＝30°，若小华的眼睛与地面的距离是1.6米，BG＝0.7米，BG平行于AC所在的直线，迎水坡i＝4∶3，坡长AB＝8米，点A、B、C、D、F、G在同一平面内，则此时小船C到岸边的距离CA的长为 米(结果保留根号)．‎ 三、解答题(共66分)‎ ‎19．(8分)计算：‎ ‎(1)10sin30°－|3tan30°－1|＋sin245°；‎ ‎(2)－5tan230°＋2.‎ ‎20．(8分)如图，在△ABC中，AD是BC边上的高，AE是BC边上的中线，∠C＝45°，sinB＝，AD＝1.‎ ‎(1)求BC的长；‎ ‎(2)求tan∠DAE的值．‎ ‎21.(6分)如图，在教学实践课中，小明为了测量学校旗杆CD的高度，在地面A处放置高度为1.5米的测角仪AB，测得旗杆顶端D的仰角为32°，AC＝22米，求旗杆CD的高度(结果精确到0.1米，参考数据：sin32°≈0.53，cos32°≈0.85，tan32°≈0.62)．‎ ‎22．(8分)如图，从热气球C上测得两建筑物A、B底部的俯角分别为30°和60°.如果这时气球的高度CD为90米，且点A、D、B在同一直线上，求建筑物A、B间的距离．‎ ‎23．(8分)已知△ABC中的∠A与∠B满足(1－tanA)2＋＝0.‎ ‎(1)试判断△ABC的形状；‎ ‎(2)求(1＋sinA)2－2－(3＋tanC)0的值．‎ ‎24．(8分)如图①是“东方之星”救援打捞现场图，小红据此构造出一个如图②所示的数学模型．已知：A、B、D三点在同一水平线上，CD⊥AD，∠A＝30°，∠CBD＝75°，AB＝60m.‎ ‎(1)求点B到AC的距离；‎ ‎(2)求线段CD的长度．‎ ‎25．(8分)如图，建筑物AB后有一座假山，其坡度为i＝1∶，山坡上E点处有一凉亭，测得假山坡脚C与建筑物水平距离BC＝25米，与凉亭距离CE＝20米，某人从建筑物顶端测得E点的俯角为45°，求建筑物AB的高．‎ ‎26．(12分)在一次科技活动中，小明进行了模拟雷达扫描实验．如图，表盘是△ABC，其中AB＝AC，∠BAC＝120°.在点A处有一束红外光线AP，从AB开始，绕点A逆时针匀速旋转，每秒钟旋转15°，到达AC后立即以相同旋转速度返回AB，到达后立即重复上述旋转过程．小明通过实验发现，光线从AB处旋转开始计时，旋转1秒，此时光线AP交BC于点 M，BM的长为(20－20)cm.‎ ‎(1)求AB的长；‎ ‎(2)从AB处旋转开始计时，若旋转6秒，此时光线AP与BC边的交点在什么位置？若旋转2014秒，交点又在什么位置？请说明理由．‎ 参考答案：‎ ‎1．A　2.A　3.D　4.B　5.D　6.D　7.C 8． D　解析：如图，延长AD，过点C作CE⊥AD，垂足为E.‎ ‎∵tanB＝，即＝，‎ ‎∴设AD＝5x，则AB＝3x.‎ ‎∵∠CDE＝∠BDA，∠CED＝∠BAD，‎ ‎∴△CDE∽△BDA，‎ ‎∴＝＝＝，‎ ‎∴CE＝x，DE＝x，‎ ‎∴AE＝x，‎ ‎∴tan∠CAD＝＝.故选D.‎ ‎9.　10.直角　11.2　12.　13.± ‎14．9　15.2(－)　16.135　17. 18． ‎(8－5.5)　解析：过点B作BE⊥AC于点E，延长DG交CA于点H，得Rt△ABE和矩形BEHG.‎ ‎∵i＝＝，AB＝8米，‎ ‎∴BE＝米，AE＝米．‎ ‎∵DG＝1.6米，BG＝0.7米，‎ ‎∴DH＝DG＋GH＝1.6＋＝8(米)，AH＝AE＋EH＝＋0.7＝5.5(米)．‎ 在Rt△CDH中，∵∠C＝∠FDC＝30°，DH＝8(米)，tan30°＝＝，‎ ‎∴CH＝8(米)．‎ 又∵CH＝CA＋5.5，即8＝CA＋5.5，‎ ‎∴CA＝(8－5.5)米．‎ ‎19．解：(1)原式＝10×－＋·＝5－(－1)＋＝6－＋；(4分)‎ ‎(2)原式＝＋1－5×＋2×＝＋1－＋2－＝.(8分)‎ ‎20．解：(1)在△ABC中，∵AD是BC边上的高，‎ ‎∴∠ADB＝∠ADC＝90°.‎ 在△ADC中，∵∠ADC＝90°，∠C＝45°，AD＝1，‎ ‎∴DC＝AD＝1.(2分)‎ 在△ADB中，∵∠ADB＝90°，sinB＝，AD＝1，‎ ‎∴AB＝＝3，‎ ‎∴BD＝＝2，‎ ‎∴BC＝BD＋DC＝2＋1；(5分)‎ (2) ‎∵AE是BC边上的中线，‎ ‎∴CE＝BC＝＋.‎ ‎∴DE＝CE－CD＝－，‎ ‎∴tan∠DAE＝＝－.(8分)‎ 21． 解：过B作BE⊥CD交CD于E.(1分)‎ 在Rt△DBE中，BE＝AC＝22米，∠DBE＝32°，‎ ‎∴DE＝BE·tan32°≈22×0.62＝13.64(米)，(4分)‎ ‎∴CD＝AB＋DE＝1.5＋13.64＝15.14≈15.1(米)．(6分)‎ 22． 解：由已知，得∠ECA＝30°，∠FCB＝60°，CD＝90，EF∥AB，CD⊥AB于点D.‎ ‎∴∠A＝∠ECA＝30°，∠B＝∠FCB＝60°.(2分)‎ 在Rt△ACD中，∠CDA＝90°，tanA＝，∴AD＝＝＝90×＝90(米)．(4分)在Rt△BCD中，∠CDB＝90°，tanB＝，∴DB＝＝＝30.(6分)‎ ‎∴AB＝AD＋BD＝90＋30＝120(米)．(7分)‎ 答：建筑物A、B间的距离为120米．(8分)‎ 21． 解：(1)∵(1－tanA)2＋＝0，‎ ‎∴tanA＝1，sinB＝，(2分)‎ ‎∴∠A＝45°，∠B＝60°，∠C＝180°－45°－60°＝75°，‎ ‎∴△ABC是锐角三角形；(4分)‎ (2) ‎∵∠A＝45°，∠B＝60°，∠C＝75°，‎ (3) ‎∴原式＝－2－1＝.(8分)‎ 22． 解：(1)过点B作BE⊥AC于点E，‎ 在Rt△AEB中，AB＝60m，sinA＝，‎ ‎∴BE＝60×＝30(m)，即B到AC的距离是30m；(4分)‎ (2) ‎∵cosA＝，∴AE＝60×＝30(m)．‎ 在Rt△CEB中，∠ACB＝∠CBD－∠A＝75°－30°＝45°，‎ ‎∴BE＝CE＝30m，‎ ‎∴AC＝AE＋CE＝(30＋30)m.(6分)‎ 在Rt△ADC中，sinA＝，则CD＝(30＋30)×＝(15＋15)(m)．(8分)‎ 23． 解：过点E作EF⊥BC于点F，EN⊥AB于点N.‎ ‎∵建筑物AB后有一座假山，其坡度为i＝1∶，‎ ‎∴设EF＝x米，则FC＝x米，(2分)‎ ‎∵CE＝20米，∴x2＋(x)2＝400，解得x＝10，则FC＝10米．(4分)‎ ‎∵BC＝25米，∴BF＝NE＝(25＋10)米，‎ ‎∴AB＝AN＋BN＝NE＋EF＝10＋25＋10＝(35＋10)(米)．(7分)‎ 答：建筑物AB的高为(35＋10)米．(8分)‎ 24． 解：(1)如图，过A作AD⊥BC，垂足为D.‎ ‎∵AB＝AC，∠BAC＝120°，‎ ‎∴∠BAD＝∠CAD＝60°，∠ABD＝30°.(2分)‎ ‎∵∠BAM＝15°，∴∠MAD＝45°.‎ 则设AD＝MD＝xcm，‎ 在△ABD中，tan∠ABD＝＝＝，解得x＝20.即MD＝AD＝20cm，AB＝2AD＝40cm.‎ 答：AB的长为40cm；(5分)‎ ‎（2）如图，旋转6秒时，设交点为N，‎ ‎∴∠BAN＝6×15°＝90°，‎ ‎∴∠DAN＝30°，∴DN＝AD＝cm.‎ ‎∴BN＝BM＋MD＋DN＝(20－20)＋20＋＝(cm)．(7分)‎ ‎∴旋转6秒，光线AP与BC边的交点在距点Bcm处．‎ 因＝8(秒)，则AP从AB旋转到AC再返回到AB需2×8＝16(秒)，2014＝125×16＋14，即AP旋转2014秒与旋转14秒时和BC的交点是同一点Q，如图．(9分)易求得CQ＝cm，BC＝40cm.∴BQ＝BC－CQ＝40－＝(cm)．∴光线AP旋转2014秒，与BC的交点Q在距点Bcm处．(12分)‎