2013年辽宁大连中考数学试卷及答案(解析版) 14页

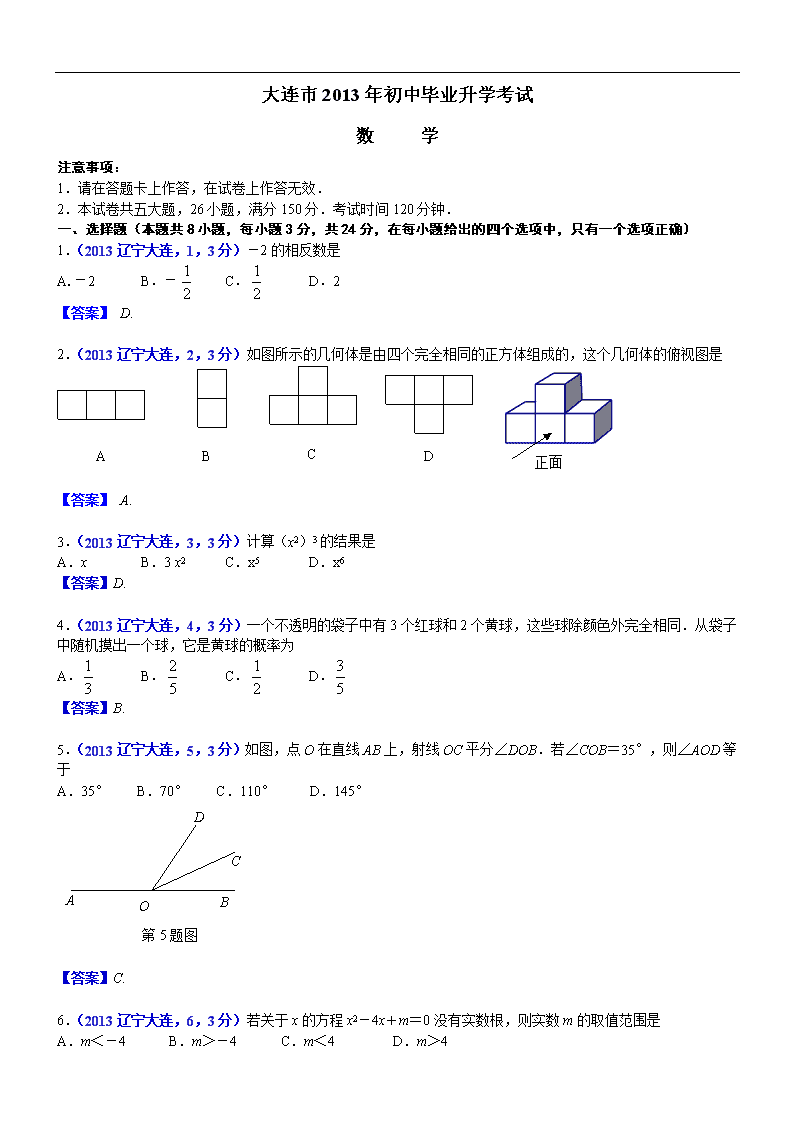
大连市2013年初中毕业升学考试 数 学 注意事项：‎ ‎1．请在答题卡上作答，在试卷上作答无效．‎ ‎2．本试卷共五大题，26小题，满分150分．考试时间120分钟．‎ 一、选择题（本题共8小题，每小题3分，共24分，在每小题给出的四个选项中，只有一个选项正确）‎ ‎1．（2013辽宁大连，1，3分）－2的相反数是 A.－2 B．－ C． D．2‎ ‎【答案】 D.‎ ‎2．（2013辽宁大连，2，3分）如图所示的几何体是由四个完全相同的正方体组成的，这个几何体的俯视图是 A B C D 正面 ‎【答案】 A.‎ ‎3．（2013辽宁大连，3，3分）计算（x2）3的结果是 A．x B．3 x‎2 ‎ C．x5 D．x6‎ ‎【答案】D.‎ ‎4．（2013辽宁大连，4，3分）一个不透明的袋子中有3个红球和2个黄球，这些球除颜色外完全相同．从袋子中随机摸出一个球，它是黄球的概率为 A． B． C． D．‎ ‎【答案】B.‎ ‎5．（2013辽宁大连，5，3分）如图，点O在直线AB上，射线OC平分∠DOB．若∠COB＝35°，则∠AOD等于 A．35° B．70° C．110° D．145°‎ O A B C D 第5题图 ‎【答案】C.‎ ‎6．（2013辽宁大连，6，3分）若关于x的方程x2－4x＋m＝0没有实数根，则实数m的取值范围是 A．m＜－4 B．m＞－‎4 ‎ C．m＜4 D．m＞4‎ ‎【答案】D.‎ ‎7．（2013辽宁大连，7，3分）在一次“爱心互助”捐款活动中，某班第一小组8名同学捐款的金额（单位：元）如下表所示：‎ 金额/元 ‎5‎ ‎6‎ ‎7‎ ‎10‎ 人数 ‎2‎ ‎3‎ ‎2‎ ‎1‎ 这8名同学捐款的平均金额为 A．3.5元 B．6元 C．6.5元 D．7元 ‎【答案】C.‎ ‎8．（2013辽宁大连，8，3分）P是∠AOB内一点，分别作点P关于直线OA、OB的对称点P1、P2，连接OP1、OP2，则下列结论正确的是 A．OP1⊥OP2 B．OP1＝OP‎2 ‎ C．OP1⊥OP2且OP1＝OP2 D．OP1≠OP2‎ ‎【答案】B.‎ 二、填空题（本题共8小题，每小题3分，共24分）‎ ‎9．（2013辽宁大连，9，3分）分解因式：x2＋x＝_________．‎ ‎【答案】x（x＋1）.‎ ‎10．（2013辽宁大连，10，3分）在平面直角坐标系中，点（2，－4）在第________象限．‎ ‎【答案】 四.‎ ‎11．（2013辽宁大连，11，3分）将16 000 000用科学记数法表示为_______________．‎ ‎【答案】 1.6×107.‎ ‎12．（2013辽宁大连，12，3分）某林业部门统计某种幼树在一定条件下的移植成活率，结果如下表所示 移植总数（n）‎ ‎400‎ ‎750‎ ‎1500‎ ‎3500‎ ‎7000‎ ‎9000‎ ‎14000‎ 成活数（m）‎ ‎369‎ ‎662‎ ‎1335‎ ‎3203‎ ‎6335‎ ‎8073‎ ‎12628‎ 成活的频率 ‎0.923‎ ‎0.883‎ ‎0.890‎ ‎0.915‎ ‎0.905‎ ‎0.897‎ ‎0.902‎ 根据表中数据，估计这种幼树移植成活的概率为_______（精确到0.1）．‎ ‎【答案】0.9.‎ ‎13．（2013辽宁大连，13，3分）化简：x＋1－＝___________．‎ ‎【答案】.‎ ‎14．（2013辽宁大连，14，3分）用一个圆心角为90°，半径为‎32 cm的扇形作为一个圆锥的侧面（接缝处不重叠），则这个圆锥的底面圆的半径为_______cm．‎ ‎【答案】8.‎ ‎15．（2013辽宁大连，15，3分）如图，为了测量河的宽度AB ，测量人员在高‎21m的建筑物CD的顶端D 处测得河岸B处的俯角为45°，测得河对岸A处的俯角为30°（A、B、C在同一条直线上），则河的宽度AB约为________m（精确到‎0.1m）．（参考数据：≈ 1.41，≈1.73）‎ D C B A ‎45°‎ ‎30°‎ 第15题图 ‎【答案】15.3.‎ ‎16．（2013辽宁大连，16，3分）如图，抛物线y＝x2＋bx＋与y轴相交于点A，与过点A平行于x轴的直线相交于点B（点B在第一象限）．抛物线的顶点C在直线OB上，对称轴与x轴相交于点D．平移抛物线，使其经过点A、D，则平移后的抛物线的解析式为_________．‎ 第16题图 ‎【答案】y＝x2－x＋.‎ 三、解答题（本题共4小题，第17、18、19题各9分，第20题12分，共39分）‎ ‎17．（2013辽宁大连，17，9分）计算：．‎ ‎ 解：＝5＋（1－3）－2＝5－2－2＝3－2．‎ ‎18. （2013辽宁大连，18，9分）解不等式组：‎ ‎ 解：解不等式①得x＞2；解不等式②得x＞4．所以不等式组的解集为x＞4．‎ ‎19. （2013辽宁大连，19，9分）如图，ABCD中，点E、F分别在AD、BC上，且AE＝CF.‎ ‎　　求证：BE＝DF.‎ 第19题图 证明：∵四边形ABCD中是平行四边形 ‎ ∴AB＝CD. ∠A＝∠C. ‎ 又∵AE＝CF.‎ ‎∴△ABE ≌△CDF ‎∴BE＝DF.‎ ‎20．（2013辽宁大连，20，12分）以下是根据《2012年大连市环境状况公报》中有关海水浴场环境质量和市区空气质量级别的数据制作的统计图表的一部分（2012年其366天） .‎ 大连市2012年海水浴场环境质量监测结果统计表 监测时段：2012年7月至9月 浴场名称 优（％）‎ 良（％）‎ 差（％）‎ 浴场1‎ ‎25‎ ‎75‎ ‎0‎ 浴场2‎ ‎30‎ ‎70‎ ‎0‎ 浴场3‎ ‎30‎ ‎70‎ ‎0‎ 浴场4‎ ‎40‎ ‎60‎ ‎0‎ 浴场5‎ ‎50‎ ‎50‎ ‎00‎ 浴场6‎ ‎30‎ ‎70‎ ‎0‎ 浴场7‎ ‎10‎ ‎90‎ ‎0‎ 浴场8‎ ‎10‎ ‎50‎ ‎40‎ O ‎50‎ ‎100‎ ‎150‎ ‎200‎ ‎250‎ ‎129‎ 优 良 污染 大连市2012年市区空气质量级别统计图 良的天数 优的天数 污染的天数 ‎3.8％‎ 人数 级别 根据以上信息，解答下列问题：‎ ‎（1）2012年7月至9月被监测的8个海水浴场环境质量最好的是_____（填浴场名称），海水浴场环境质量为优的数据的众数为______％，海水浴场环境质量为良的数据的中位数为____％；‎ ‎（2）2012年大连市区空气质量达到优的天数为_____天，占全年（366天）的百分比约为_____（精确到0.1％）；‎ ‎（3）求2012年大连市区空气质量为良的天数（按四舍五入，精确到个位）．‎ ‎【解】（1）浴场5；30；70；（2）129；35.2；（3）1－35.2％－3.8％＝61％，366×61％≈223（天）．答：2012年大连市区空气质量为良的天数为223天．‎ 四、解答题（本题共3小题，其中21、22题各9分，23题10分，共28分）‎ ‎21．（2013辽宁大连，21，9分）某超市购进A、B两种糖果，A种糖果用了480元，B种糖果用了1260元，A、B两种糖果的重量比是1：3，A种糖果每千克的进价比B种糖果每千克的进价多2元．A、B两种糖果各购进多少千克?‎ ‎ 解：设A种糖果购进x千克，则B种糖果购进3x千克，根据题意列方程，得 ‎ ‎ 解得x＝30‎ 经检验，x＝30是原方程的解，且符合题意．‎ ‎3x＝90‎ 答：A种糖果购进30千克，B种糖果购进90千克．‎ ‎22．（2013辽宁大连，22，9分）如图，在平面直角坐标系xOy中，一次函数y＝ax＋b的图象与反比例函数y＝的图象相交于点A（m，1）、B（－1，n），与x轴相交于点C（2，0），且AC＝OC．‎ ‎ （1）求该反比例函数和一次函数的解析式；‎ ‎（2）直接写出不等式ax＋b≥的解集．‎ O A B C x y 第22题图 ‎（1）解：过点A作AD⊥x轴，垂足为D，则AD＝1．‎ 在Rt△ACD中，CD＝．‎ ‎∴点A的坐标为（3，1）．‎ ‎∴1＝，k＝3．‎ ‎∴反比例函数的解析式为y＝． ‎ 由题意得 解得 ‎∴一次函数的解析式为y＝x－2‎ ‎（2）不等式ax＋b≥的解集为－1≤x＜0或x≥3．‎ O A B C x y 第22题图 D ‎ 23．（2013辽宁大连，23，10分）如图，AB是⊙O的直径，CD与⊙O相切于点C，DA⊥AB，DO及DO的延长线与⊙O分别相交于点E、F，EB与CF相交于点G．‎ ‎（1）求证：DA＝DC；‎ ‎（2） ⊙O的半径为3，DC＝4，求CG的长．‎ O D A B C F G E 第23题图 ‎（1）证明： AB是⊙O的直径，DA⊥AB ‎∴DA是⊙O的切线.‎ ‎∵DC是⊙O的切线，‎ ‎∴DA＝DC.‎ ‎（2）解：连接AC、OC，AC与DO相交于点H.‎ ‎∵DA＝DC， AO＝CO，DO＝DO，‎ ‎∴△AOD≌△COD.‎ ‎∴∠AOD＝∠COD.‎ ‎∴OD是AC的垂直平分线.‎ ‎∵∠AHO＝∠DAO，∠AOH＝∠DOA.‎ ‎∴△AOH∽△DOA.‎ ‎∴，即.‎ ‎∴OH＝，AH＝＝CH.‎ 在Rt△CHF中，CF＝＝.‎ ‎∵O、H分别是AB、AC的中点，‎ ‎∴BC＝2OH＝.‎ 又∵∠CFE＝∠CBE＝∠COE＝∠AOE＝∠BOF＝∠BEF＝∠BCF，‎ ‎∴△EFG∽△BCG.‎ ‎∴，即5CG＝3FG＝3（－CG）.‎ ‎∴CG＝.‎ O D A B C F G E H 五、解答题（本题共3小题，其中24题11分，25、26题各12分，共35分）‎ ‎24．（2013辽宁大连，24，11分）如图，一次函数y＝－x＋4的图象与x轴、y轴分别相交于点A、B，P是射线BO上的一个动点（点P不与点B重合），过点P作PC⊥AB，垂足为C，在射线CA上截取CD＝CP．连接PD，设BP＝t．‎ ‎（1）t为何值时，点D恰好与点A重合?‎ ‎（2）设△PCD与△AOB重叠部分的面积为s，求s与t的函数关系式，并直接写出t的取值范围．‎ O A B C D P x y 第24题图 解：（1）如图1，由y＝－x＋4知：当x＝0时，y＝4；当y＝0时，x＝3.‎ ‎∴OA＝3，OB＝4，AB＝5.‎ ‎∵∠PCB＝∠AOB＝90°,∠PBO＝∠ABO，‎ ‎∴△PCB∽△AOB.‎ ‎∴，即.‎ ‎∴PC＝，BC＝.‎ 当点D与点A重合时，BC＋CD＝BA，即＋=5.‎ ‎ ∴t＝.‎ O A B C D P x y 第24题图1‎ ‎（2）当0＜t≤时（如图1），S＝PC·CD＝×（）2＝t2.‎ 当＜t≤4时，（如图2），设PD与x轴相交于点E，作EF⊥CD，垂足为F.‎ 由（1）知AD＝BC＋CD－BA＝＋－5＝－5.‎ ‎∵∠EFA＝∠BOA，∠EAF＝∠BAO，‎ ‎∴△AFE∽△AOB.‎ ‎∴，即EF＝AF＝（FD－AD）.‎ ‎∵CD＝CP，∠PCD＝90°，‎ ‎∴∠PDC＝∠DPC＝45°＝90°－∠DEF.‎ ‎∴∠DEF＝45°＝∠FDE.‎ ‎∴FD＝EF＝（FD－AD）＝［EF－（－5）］.‎ ‎∴EF＝4（－5）.‎ ‎∴S＝PC·CD－AD·EF＝t2－(－5)×4（－5）＝－t2＋28t－50.‎ O A B C D P x y 第24题图2‎ E F 当4＜t＜时（如图3），设PC与x轴相交于点E.则AC＝AB－BC＝5－t.‎ 同理EC＝AC＝（5－t）.‎ ‎∴S＝AC·EC＝（5－t）×（5－t）＝－t＋.‎ O A B C D P x y 第24题图3‎ E 综上，S＝．‎ ‎25. （2013辽宁大连，25，12分）将△ABC绕点Ｂ逆时针旋转α得到△DBE，DE的延长线与AC相交于点Ｆ，连接DA、BF.‎ ‎（1）如图１，若∠ABC＝α＝60°，BF＝AF.‎ ‎①求证：DA∥BC；②猜想线段DF、AF的数量关系，并证明你的猜想； ‎ ‎（2）如图2，若∠ABC＜α，BF＝mAF（m为常数），求的值（用含m、α的式子表示）。 ‎ 第25题图1‎ 第25题图2‎ ‎（1）①证明：如图1，由题意知，点E在AB上，DB＝AB，∠DBA＝∠ABC＝60°.‎ ‎∴△DBA是等边三角形.‎ ‎∴∠DAB＝60°＝∠ABC.‎ ‎∴DA∥BC.‎ ‎②猜想：DF＝2AF.‎ 证明：在DF上截取DG＝AF，连接BG（如图1）‎ 由已知得DB＝AB，∠BDG＝∠BAF，‎ ‎∴△DBG≌△ABF.‎ ‎∴BG＝BF，∠BDG＝∠BAF.‎ ‎∴∠GBF＝∠GBE＋∠EBF＝∠GBE＋∠DBG＝∠DBE＝60°.‎ ‎∴△GBF是等边三角形.‎ ‎∴GF＝BF.‎ ‎∵BF＝AF.‎ ‎∴GF＝AF.‎ ‎∴DF＝DG＋GF＝AF＋AF＝2AF.‎ 第25题图1‎ G ‎（2）解：在DF上截取DG＝AF，连接BG，作BH⊥DF，垂足为H（如图）.‎ 由（1）知BG＝BF，∠DBG＝∠ABF.‎ ‎∴GH＝HF＝GF.‎ ‎∠HBF＝（∠GBA＋∠ABF）＝（∠GBA＋∠DBG）＝∠DBA＝.‎ 在Rt△HBF中，HF＝BF·sin∠HBF＝mAF·sin，‎ ‎∴＝1＋2msin．‎ 第25题图2‎ G F ‎26．（2013辽宁大连，26，12分）如图，抛物线y＝－x2＋x－4与x轴相交于点A、B，与y轴相交于点C，抛物线的对称轴与x轴相交于点M．P是抛物线在x轴上方的一个动点（点P、M、C不在同一条直线上） ．分别过点A、B作直线CP的垂线，垂足分别为D、E，连接MD、ME．‎ ‎（1）求点A、B的坐标（直接写出结果），并证明△MDE是等腰三角形；‎ ‎（2）△MDE能否为等腰直角三角形?若能，求此时点P的坐标，若不能，说明理由；‎ ‎（3）若将“P是抛物线在x轴上方的一个动点（点P、M、C不在同一条直线上）”改为“P是抛物线在x轴下方的一个动点”，其他条件不变，△MDE能否为等腰直角三角形?若能，求此时点P的坐标（直接写出结果），若不能，说明理由．‎ O A B C D E P M x y 第26题图 y x O A B M C 备用图 解：（1）点A、B的坐标分别为（1，0）、（5，0）.‎ 证明：如图1，延长DM与EB相交于点F. ‎ ‎∵AD⊥CP，BE⊥CP.‎ ‎∴∠ADE＝∠BED＝90°.‎ ‎∴AD∥EB.‎ ‎∴∠DAM＝∠FBM，∠MDA＝∠MFB.‎ 由题意知AM＝BM，‎ ‎∴△ADM≌△BPM.‎ ‎∴DM＝FM＝DF.‎ ‎∵∠DEF＝90°.‎ ‎∴EM＝DF.‎ ‎∴DM＝EM，即△MDE是等腰三角形.‎ O A B C D E P M x y 第26题图1‎ F ‎（2）能.理由如下：‎ 如图2，若△MDE为等腰直角三角形，则DM＝EM，∠DME＝∠MED＝45°.‎ 设直线CP与对称轴相交于点G，则∠MEG＝180°－∠MED＝135°.‎ ‎∴∠MDA＝∠ADG＋∠MDE＝90°＋45°＝135°＝∠MEG.‎ ‎∵∠DMA＝90°－∠AME＝∠EMG.‎ ‎∴△AMD≌△GME.‎ ‎∴GM＝AM＝AB＝2，即点G的坐标为（3，2）.‎ 设直线CP的解析式为y＝kx＋b，即 ，解得.‎ ‎∴y＝2x－4.‎ 设点P的坐标为（m，‎2m－4），则－m2＋m－4＝‎2m－4.‎ 解得m1＝0（舍），m2＝.‎ 当m＝时，y＝2×－4＝3.即点P的坐标为（，3）. ‎ y x O A B M C 第26题图2‎ D E F G P ‎（3）能.点P的坐标为（，－）．‎