中考数学一轮复习知识点+题型专题讲义20 勾股定理（教师版） 24页

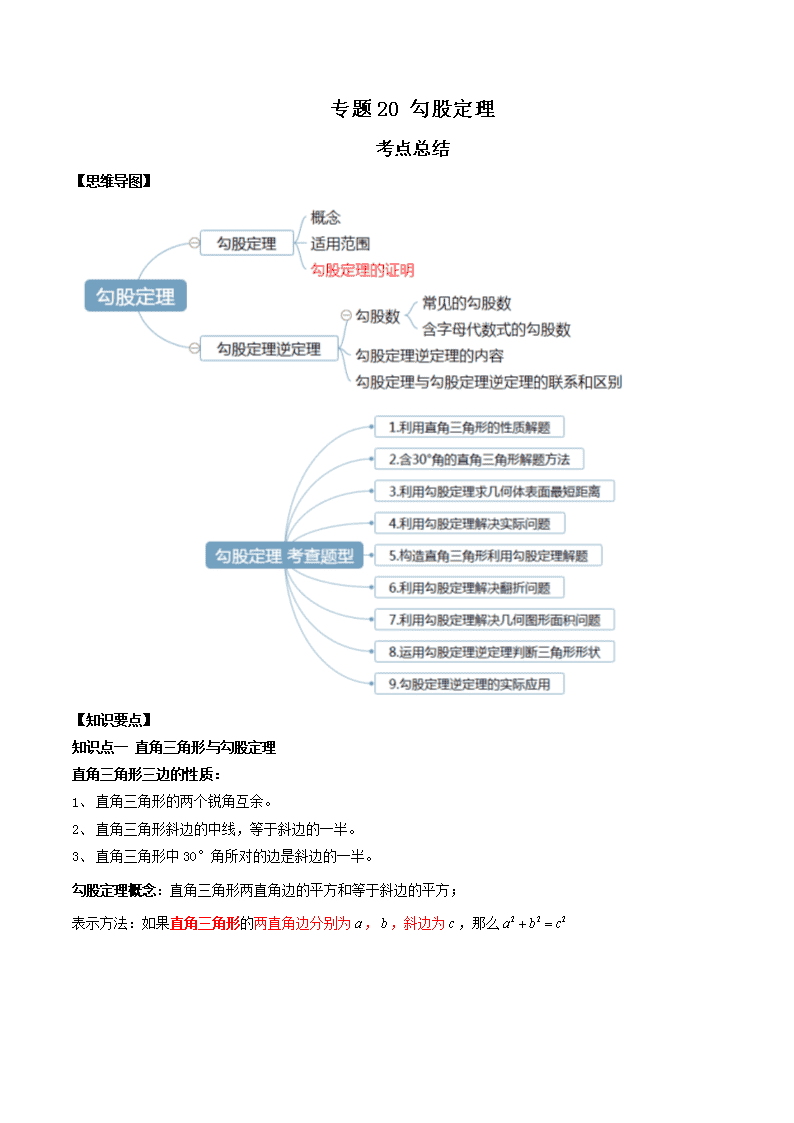
专题 20 勾股定理 考点总结 【思维导图】 【知识要点】 知识点一 直角三角形与勾股定理 直角三角形三边的性质： 1、 直角三角形的两个锐角互余。 2、 直角三角形斜边的中线，等于斜边的一半。 3、 直角三角形中 30°角所对的边是斜边的一半。 勾股定理概念：直角三角形两直角边的平方和等于斜边的平方； 表示方法：如果直角三角形的两直角边分别为 a ， b ，斜边为 c ，那么 2 2 2a b c  变式： 1）a²=c²- b² 2）b²=c²- a² 适用范围：勾股定理揭示了直角三角形三条边之间所存在的数量关系，它只适用于直角三角形，因而在应 用勾股定理时，必须明了所考察的对象是直角三角形。 勾股定理的证明： 勾股定理的证明方法很多，常见的是拼图的方法 用拼图的方法验证勾股定理的思路是： ①图形进过割补拼接后，只要没有重叠，没有空隙，面积不会改变 ②根据同一种图形的面积不同的表示方法，列出等式，推导出勾股定理 方法一： 4 EFGHS S S  正方形 正方形ABCD ， 2 214 ( )2 ab b a c    ，化简可证． 方法二： 四个直角三角形的面积与小正方形面积的和等于大正方形的面积． 四个直角三角形的面积与小正方形面积的和为 2 214 22S ab c ab c     大正方形面积为 2 2 2( ) 2S a b a ab b     所以 2 2 2a b c  方法三： 1 ( ) ( )2S a b a b   梯形 ， 21 12S 2 2 2ADE ABES S ab c     梯形 ，化简得证 2 2 2a b c  【考查题型汇总】 考查题型一 利用直角三角形的性质解题 1．（2018·湖南中考模拟）如图，在△ABC 中，AB=AC，∠BAC=120°，EF 为 AB 的垂直平分线，交 BC 于 点 F，交 AB 于点 E．求证：FC=2BF． 【答案】见解析 【详解】 证明：连接 AF， ∵EF 为 AB 的垂直平分线， ∴AF=BF， 又 AB=AC，∠BAC=120°， ∴∠B=∠C=∠BAF=30°， ∴∠FAC=90°， ∴AF= FC， ∴FC=2BF． 2.（2013·江苏中考模拟）如图，在 Rt△ABC 中，∠C＝90°，AC＝ 3 ，点 D 为 BC 边上一点，且 BD＝2AD， ∠ADC＝60°，求△ABC 的周长(结果保留根号)． 【答案】 2 7 5 3  ； 21 7 【解析】 在 Rt△ADC 中，∠C＝90°， 3AC  ，∠ADC＝60°， 因为 sin ACADC AD   ，即 3 3 2AD  ，所以 AD＝2． 由勾股定理得： 2 2 1DC AD AC   ． 所以 BD＝2AD＝4，BC＝BD＋DC＝5． 在 Rt△ABC 中，∠C＝90°， 3AC  ，BC＝5， 由勾股定理得： 2 2 2 7AB BC AC   ， 所以 Rt△ABC 的周长为 2 7 5 3AB BC AC     ． 3．（2019·江苏中考模拟）如图，在△ABC 中，AB=AC，∠BAC=120°，D 为 BC 的中点，DE⊥AB 于 E， 求 EB：EA 的值． 【答案】3 【详解】如图，连接 AD， ∵AB=AC，∠BAC=120°，D 为 BC 的中点， ∴∠BAD=60°，AD⊥BC， ∴∠B=90°﹣60°=30°， ∵DE⊥AB， ∴∠ADE=90°﹣60°=30°， 设 EA=x， 在 Rt△ADE 中，AD=2EA=2x， 在 Rt△ABD 中，AB=2AD=4x， ∴EB=AB﹣EA=4x﹣x=3x， ∴EB：EA=3x：x=3． 考查题型二 含 30°角的直角三角形解题方法 1．（2018·黑龙江中考模拟）如图，在△ABC 中，AB=AC，∠C=30°，AB⊥AD，AD=4，则 BC 的长为（ ） A．4 B．8 C．12 D．16 【答案】C 【详解】 ∵AB=AC，∠C=30°， ∴∠B=∠C=30°， ∴∠BAC=120°， ∵AB⊥AD，AD=4， ∴∠BAD=90°，BD=2AD=8， ∴∠DAC=120°-90°=30°， ∴∠DAC =∠C=30°， ∴AD=CD=4， ∴CB=DB+CD=12． 故选 C. 2．（2019·丹东市第十七中学中考模拟）如图，在 Rt△ABC 中，CM 平分∠ACB 交 AB 于点 M，过点 M 作 MN∥BC 交 AC 于点 N，且 MN 平分∠AMC，若 AN=1，则 BC 的长为（ ） A．4 B．6 C． 4 3 D．8 【答案】B 【解析】 ∵在 Rt△ABC 中，CM 平分∠ACB 交 AB 于点 M，过点 M 作 MN∥BC 交 AC 于点 N，且 MN 平分∠AMC， ∴∠AMN=∠NMC=∠B，∠NCM=∠BCM=∠NMC， ∴∠ACB=2∠B，NM=NC， ∴∠B=30°， ∵AN=1， ∴MN=2， ∴AC=AN+NC=3， ∴BC=6， 故选 B． 3．（2018·湖北中考模拟）如图,在△ABC 中,∠C=90°,∠B=30°,AD 平分∠CAB 交 BC 于点 D,E 为 AB 上一点, 连接 DE,则下列说法错误的是( ) A．∠CAD=30° B．AD=BD C．BD=2CD D．CD=ED 【答案】D 【解析】 试题分析：在△ABC 中， ∵∠C=90°，∠B=30°， ∴∠CAB=60°， ∵AD 平分∠CAB， ∴∠CAD=∠BAD=30°， ∴∠CAD=∠BAD=∠B， ∴AD=BD，AD=2CD， ∴BD=2CD， 根据已知不能推出 CD=DE， 只有 D 错误，选项 A、B、C 的答案都正确． 故选 D． 4．（2018·安徽中考模拟）如图，在 Rt△ABC 中，∠C=90°，∠CAB 的平分线交 BC 于 D，DE 是 AB 的垂 直平分线，垂足为 E，若 BC=3，则 DE 的长为（ ） A．1 B．2 C．3 D．4 【答案】A 【解析】 由角平分线和线段垂直平分线的性质可求得∠B=∠CAD=∠DAB=30°， ∵DE 垂直平分 AB， ∴DA=DB，∴∠B=∠DAB，∵AD 平分∠CAB，∴∠CAD=∠DAB， ∵∠C=90°，∴3∠CAD=90°， ∴∠CAD=30°， ∵AD 平分∠CAB，DE⊥AB，CD⊥AC， ∴CD=DE= BD， ∵BC=3， ∴CD=DE=1 考查题型三 利用勾股定理求几何体表面最短距离 1．（2017·河北中考模拟）如图，一只蚂蚁沿边长为 a 的正方体表面从点 A 爬到点 B，则它走过的路程最短 为（ ） A． 2 a B．（1+ 2 ）a C．3a D． 5 a 【答案】D 【解析】 详解：如图，则 AB= 2 2AP PB = 2 24a a = 5 a． 故选 D． 2．（2016·山东中考模拟）如图，透明的圆柱形容器(容器厚度忽略不计)的高为 12cm，底面周长为 10cm， 在容器内壁离容器底部 3cm 的点 B 处有一饭粒，此时一只蚂蚁正好在容器外壁，且离容器上沿 3cm 的点 A 处，则蚂蚁吃到饭粒需爬行的最短路径是( ) A．13cm B．2 R cm C． R cm D．2 cm 【答案】A 【解析】 试题解析：如图： ∵高为 12cm，底面周长为 10cm，在容器内壁离容器底部 3cm 的点 B 处有一饭粒， 此时蚂蚁正好在容器外壁，离容器上沿 3cm 与饭粒相对的点 A 处， ∴A′D=5cm，BD=12-3+AE=12cm， ∴将容器侧面展开，作 A 关于 EF 的对称点 A′， 连接 A′B，则 A′B 即为最短距离， A′B= R R （cm）． 故选 A． 3．（2018·南宫市奋飞中学中考模拟）如图,在底面周长为 12,高为 8 的圆柱体上有 A,B 两点,若沿圆柱的侧面 积运动，则 AB 之间的最短距离是( ) A．10 B．3 C．5 D．4 【答案】A 【解析】 展开圆柱的半个侧面，得到一个矩形：矩形的长是圆柱底面周长的一半是 6， 矩形的宽是圆柱的高是 8． 根据勾股定理求得矩形的对角线是 10． 即 A、B 两点间的最短距离是 10． 故选 C． 考查题型四 利用勾股定理解决实际问题 1．（2019·重庆市全善学校中考模拟）如图，在高为 3 米，斜坡长为 5 米的楼梯台阶上铺地毯，则地毯的长 度至少要（ ） A．4 米 B．5 米 C．6 米 D．7 米 【答案】D 【详解】 在 Rt△ABC 中，∠C=90°，AB=5，BC=3， ∴AC＝ 2 2AB BC ＝4 米， ∴可得地毯长度＝AC+BC＝7 米， 故选 D． 2．（2019·福建中考模拟）《九章算术》中的“折竹抵地”问题上：今有竹高一丈，末折抵地，去本六尺。问折 高几何？意思是：如图，一根竹子，原高一丈（一丈=10 尺），一阵风将竹子折断，其竹梢恰好抵地，抵地 处离竹子底部 6 尺远。问折断处离地面的高度是多少？设折断处离地面的高度为 x 尺，则可列方程为（ ） A． R香 B． R香 C．x2+6=(10-x)2 D．x2+62=(10-x)2 【答案】D 【详解】 解：如图，设折断处离地面的高度为 x 尺，则 AB=10-x，BC=6， 在 Rt△ABC 中，AC2+BC2=AB2，即 x2+62=（10-x）2． 故选：D． 3．（2019·湖北中考模拟）从电线杆离地面 8 米处拉一根长为 10m 的缆绳，这条缆绳在地面的固定点距离电 线杆底部有( )m． A．2 B．4 C．6 D．8 【答案】C 【详解】 解：由题意得，在 Rt△ABC 中，AC＝8，AB＝10， 所以 BC＝ 2 210 -8 ＝6． 故选：C． 4．（2019·湖北中考真题）在一次海上救援中，两艘专业救助船 ,A B 同时收到某事故渔船的求救讯息，已知 此时救助船 B 在 A 的正北方向，事故渔船 P 在救助船 A 的北偏西 30°方向上，在救助船 B 的西南方向上， 且事故渔船 P 与救助船 A 相距 120 海里． （1）求收到求救讯息时事故渔船 P 与救助船 B 之间的距离； （2）若救助船 A，B 分别以 40 海里/小时、30 海里/小时的速度同时出发，匀速直线前往事故渔船 P 处搜救， 试通过计算判断哪艘船先到达． 【答案】（1）收到求救讯息时事故渔船 P 与救助船 B 之间的距离为 60 2 海里；（2）救助船 B 先到达． 【详解】 (1)如图，作 PC AB 于C ， 则 90PCA PCB     ， 由题意得： =120PA 海里， =30A  ， =45BPC  ， ∴ 1 602PC PA  海里， BCP 是等腰直角三角形， ∴ 60BC PC  海里， 2 2 60 2PB PC BC   海里， 答：收到求救讯息时事故渔船 P 与救助船 B 之间的距离为 60 2 海里； (2)∵ 120PA  海里， 60 2PB  海里，救助船 ,A B 分别以 40 海里/小时、30 海里/小时的速度同时出发， ∴救助船 A 所用的时间为 120 =340 (小时)， 救助船 B 所用的时间为 60 2 2 230  (小时)， ∵3 2 2 ， ∴救助船 B 先到达． 考查题型五 构造直角三角形利用勾股定理解题 1．（2019·山东中考模拟）在△ABC 中，AB=10，AC=2 10 ，BC 边上的高 AD=6，则另一边 BC 等于（ ） A．10 B．8 C．6 或 10 D．8 或 10 【答案】C 【详解】 分两种情况： 在图①中，由勾股定理，得 2 2 2 2BD B AD 10 6 8A     ; 2 2 2 2CD (2 10) 6 2AC AD     ; ∴BC＝BD＋CD＝8＋2＝10. 在图②中，由勾股定理，得 2 2 2 2BD B AD 10 6 8A     ; 2 2 2 2CD (2 10) 6 2AC AD     ; ∴BC＝BD―CD＝8―2＝6. 故选 C. 2．（2015·河北中考模拟）在△ABC 中，若 AC=15，BC=13，AB 边上的高 CD=12，则△ABC 的周长为（ ） A．32 B．42 C．32 或 42 D．以上都不对 【答案】C 【解析】 试题分析：∵AC=15，BC=13，AB 边上的高 CD=12， ∴AD= R R ， BD= R R ， 如图 1，CD 在△ABC 内部时，AB=AD+BD=9+5=14， 此时，△ABC 的周长=14+13+15=42， 如图 2，CD 在△ABC 外部时，AB=AD-BD=9-5=4， 此时，△ABC 的周长=4+13+15=32， 综上所述，△ABC 的周长为 32 或 42． 故选 C． 3．（2018·甘肃中考模拟）如图所示，在 Rt△ABC 中，AB=CB，ED⊥CB，垂足为 D 点，且∠CED=60°， ∠EAB=30°，AE=2，求 CB 的长． 【答案】1+ 3 【解析】 过 E 点作 EF⊥AB，垂足为 F． ∵∠EAB=30°，AE=2，∴EF=BD=1． 又∵∠CED=60°，∴∠ECD=30°． ∵AB=CB，∴∠EAC=∠ECA=15°，∴AE=CE=2． 在 Rt△CDE 中，∠ECD=30°，∴ED=1，CD= 2 22 1 = 3 ， ∴CB=CD+BD=1+ 3 ． 考查题型六 利用勾股定理解决翻折问题 1．（2019·浙江省杭州第七中学中考模拟）如图，在直角坐标系中，将矩形 OABC 沿 OB 对折，使点 A 落在 A1 处，已知 OA= 3 ，AB=1，则点 A1 的坐标是（ ） A．( 3 2 ， 3 2 ) B．( 3 2 ，3) C．( 3 2 ， 3 2 ) D．( 1 2 ， 3 2 ) 【答案】A 【解析】 过 A1 作 A1D⊥OA， ∵OA＝ 3 ，AB＝1， ∴在 Rt△OAB 中，OB＝ 2 2( 3) 1 ＝2，AB＝1， ∴AB＝ 1 2 OB， ∵△AOB 是直角三角形， ∴∠AOB＝30°， OB 为折痕， ∴∠A1OB＝∠AOB＝30°，OA1＝OA＝ 3 ， Rt△OA1D 中，∠OA1D＝30°， ∴OD＝ 1 2 × 3 ＝ 3 2 ， A1D＝ 3 2 × 3 = 3 2 ∴点 A1 的坐标（ 3 2 ， 3 2 ）． 故选 A． 2．（2019·云南中考模拟）如图，将长方形纸片 ABCD 折叠，使边 DC 落在对角线 AC 上，折痕为 CE，且 D 点落在对角线 D′处．若 AB=3，AD=4，则 ED 的长为 A． 3 2 B．3 C．1 D． 4 3 【答案】A 【详解】 ∵AB=3，AD=4，∴DC=3 ∴根据勾股定理得 AC=5 根据折叠可得：△DEC≌△D′EC， ∴D′C=DC=3，DE=D′E 设 ED=x，则 D′E=x，AD′=AC﹣CD′=2，AE=4﹣x， 在 Rt△AED′中：（AD′）2+（ED′）2=AE2，即 22+x2=（4﹣x）2， 解得：x= 3 2 故选 A. 3．（2019·四川中考模拟）如图，长方形 ABCD 中 3cmAB  ， 9cmAD  ，将此长方形折叠，使点 D 与 B 点重合，折痕为 EF ，则 ABE 的面积为（ ） A． 26cm B． 28cm C． 210cm D． 212cm 【答案】A 【详解】 将此长方形折叠，使点 B 与点 D 重合， ∴BE=ED． ∵AD=9cm=AE+DE=AE+BE． ∴BE=9-AE， 根据勾股定理可知：AB2+AE2=BE2． 即 32+AE2=（9-AE）2 解得 AE=4． ∴△ABE 的面积为 3×4÷2=6． 故选 A． 考查题型七 利用勾股定理解决几何图形面积问题 1.（2017·山东中考模拟）如图，在长方形 ABCD 中，AB=8，BC=4，将长方形沿 AC 折叠，则重叠部分△ AFC 的面积为（ ） A．12 B．10 C．8 D．6 【答案】B 【解析】 试题解析：易证△AFD′≌△CFB， ∴D′F=BF， 设 D′F=x，则 AF=8-x， 在 Rt△AFD′中，（8-x）2=x2+42， 解之得：x=3， ∴AF=AB-FB=8-3=5， ∴S△AFC= 1 2 •AF•BC=10． 故选 B． 2．（2018·江苏省泰兴市济川中学中考模拟）如图，矩形 ABCD 中，AB＝4cm，BC＝8cm，如果将该矩形沿 对角线 BD 折叠，那么图中阴影部分的面积（ ）cm2. A．8 B．10 C．15 D．20 【答案】B 【解析】 根据折叠可得：∠CBD=∠EBD， ∵AD∥BC， ∴∠EDB=∠CBD， ∴∠EDB=∠EBD， ∴BE=DE， 设 BE=DE=x，则 AE=8－x，根据 Rt△ABE 的勾股定理可得：x=5， 即 DE=5，则 S 阴影=5×4÷2=10，故选 B． 3．（2018·福建中考模拟）如图，两个较大正方形的面积分别为 225，289，则字母 A 所代表的正方形的边长 为（ ） A．64 B．16 C．8 D．4 【答案】C 【详解】 解：由勾股定理得，正方形 A 的面积=289-225=64， ∴字母 A 所代表的正方形的边长为 64 =8， 故选：C． 4．（2019·广西中考模拟）如图,已知点 E 在正方形 ABCD 内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积 是( ) A．48 B．60 C．76 D．80 【答案】C 【解析】 ∵∠AEB=90°，AE=6，BE=8， ∴AB= 2 2 2 26 8 10AE BE    ∴S 阴影部分=S 正方形 ABCD-SRt△ABE=102- 1 6 82   =100-24 =76. 故选 C. 知识点二 勾股定理的逆定理 勾股数概念：能够构成直角三角形的三边长的三个正整数称为勾股数，即 2 2 2a b c  中， a ，b ， c 为正整 数时，称 a ，b ， c 为一组勾股数 常见的勾股数：如 3,4,5 ； 6,8,10 ； 5,12,13 ； 7,24,25 等 扩展：用含字母的代数式表示 n 组勾股数： 1） 2 21,2 , 1n n n  （ 2,n  n 为正整数）； 2） 2 22 1,2 2 ,2 2 1n n n n n    （ n 为正整数） 3） 2 2 2 2,2 ,m n mn m n  （ ,m n m ， n 为正整数） 注意：每组勾股数的相同整数倍，也是勾股数。 勾股定理的逆定理内容：如果三角形三边长 a ，b ， c 满足 2 2 2a b c  ，那么这个三角形是直角三角形，其 中 c 为斜边 注意： ①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法，它通过“数转化为形”来确定三角 形的可能形状，在运用这一定理时，可用两小边的平方和 2 2a b 与较长边的平方 2c 作比较，若它们相等时， 以 a ， b ， c 为三边的三角形是直角三角形；若 2 2 2a b c  ，时，以 a ， b ， c 为三边的三角形是钝角三角 形；若 2 2 2a b c  ，时，以 a ， b ， c 为三边的三角形是锐角三角形； ②定理中 a ， b ， c 及 2 2 2a b c  只是一种表现形式，不可认为是唯一的，如若三角形三边长 a ， b ， c 满 足 2 2 2a c b  ，那么以 a ， b ， c 为三边的三角形是直角三角形，但是 b 为斜边 ③勾股定理的逆定理在用问题描述时，不能说成：当斜边的平方等于两条直角边的平方和时，这个三角形 是直角三角形 勾股定理与勾股定理逆定理的区别和联系： 联系： 1、 两者都与直角三角形三边有关，且都与直角三角形有关。 2、 两者是互逆定理。 区别： 1、 两者的条件与结论相反。 2、 勾股定理是直角三角形的性质，勾股定理逆定理是直角三角形的判定方法。 【考查题型汇总】 考查题型八 运用勾股定理逆定理判断三角形形状 1．（2018·山东中考模拟）已知 a、b、c 是△ABC 的三边长，且方程 a（1+x2）+2bx﹣c（1﹣x2）=0 的两根 相等，则△ABC 为（ ） A．等腰三角形 B．直角三角形 C．等边三角形 D．任意三角形 【答案】B 【详解】原方程整理得（a+c）x2+2bx+a-c=0， 因为两根相等， 所以△=b2-4ac=（2b）2-4×（a+c）×（a-c）=4b2+4c2-4a2=0， 即 b2+c2=a2， 所以△ABC 是直角三角形， 故选 B. 2．（2018·南宫市奋飞中学中考模拟）若△ABC 三边长 a，b，c 满足 25a b  +| 1b a  |+( 5c  )2=0，则 △ABC 是( ) A．等腰三角形 B．等边三角形 C．直角三角形 D．等腰直角三角形 【答案】C 【详解】 ∵ 25a b  +|b-a-1|+(c-5)2=0， ∴a+b-25=0，b-a-1=0，c-5=0， ∴a=12，b=13，c=5， ∵ 2 2 2 169a c b   ， ∴△ABC 是直角三角形. 故选 C. 3．（2019·内蒙古中考真题）如图，在 ABC△ 中，内角 、 、A B C 所对的边分别为 a b c、 、 ． （1）若 6, 8, 12a b c＝ ＝ ＝ ，请直接写出 A 与 BÐ 的和与 C 的大小关系； （2）求证： ABC△ 的内角和等于180 ； （3）若  1 2 a b ca a b c c     ，求证： ABC△ 是直角三角形． 【答案】（1） A B C   ＜ ；（2）证明见解析；（3）证明见解析 【详解】 1（）∵在 ABC△ 中， a 6 b 8 c 12＝ ， ＝ ， ＝ ， A B C    ＜ ； 2（ ）如图，过点 A 作 MN / /BC ， MN / /BC∵ ， MAB B NAC C    ＝ ， ＝ （两直线平行，同位角相等）， MAB BAC NAC 180    ∵ ＝ （平角的定义）， B BAC C 180     ＝ （等量代换）， 即：三角形三个内角的和等于180； （3）  1 a b ca 2 a b c c     ∵ ，   2 2 21 1ac a b c a b c a 2ac c b2 2         ＝ （ ） ﹣ ＝ （ ） ， 2 2 22ac a 2ac c b  ＝ ﹣ ， 2 2 2a c b  ＝ ， ABC 是直角三角形． 考查题型九 勾股定理逆定理的实际应用 1．（2019·四川中考模拟）我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题：“问有沙田 一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形 沙田，三条边长分别为 5 里，12 里，13 里，问这块沙田面积有多大？题中“里”是我国市制长度单位，1 里 =500 米，则该沙田的面积为（ ） A．7.5 平方千米 B．15 平方千米 C．75 平方千米 D．750 平方千米 【答案】A 【解析】 ∵52+122=132， ∴三条边长分别为 5 里，12 里，13 里，构成了直角三角形， ∴这块沙田面积为： 1 2 ×5×500×12×500=7500000（平方米）=7.5（平方千米）． 故选：A． 2．（2016·河北中考模拟）一艘轮船和一艘渔船同时沿各自的航向从港口 O 出发，如图所示，轮船从港口 O 沿北偏西 20°的方向行 60 海里到达点 M 处，同一时刻渔船已航行到与港口 O 相距 80 海里的点 N 处，若 M、 N 两点相距 100 海里，则∠NOF 的度数为（ ） A．50° B．60° C．70° D．80° 【答案】C 【解析】 ∵OM=60 海里，ON=80 海里，MN=100 海里， ∴OM2+ON2=MN2，∴∠MON=90°， ∵∠EOM=20°， ∴∠NOF=180°﹣20°﹣90°=70°．故选 C． 3．（2019·湖北中考真题）在一次海上救援中，两艘专业救助船 ,A B 同时收到某事故渔船的求救讯息，已知 此时救助船 B 在 A 的正北方向，事故渔船 P 在救助船 A 的北偏西 30°方向上，在救助船 B 的西南方向上， 且事故渔船 P 与救助船 A 相距 120 海里． （1）求收到求救讯息时事故渔船 P 与救助船 B 之间的距离； （2）若救助船 A，B 分别以 40 海里/小时、30 海里/小时的速度同时出发，匀速直线前往事故渔船 P 处搜救， 试通过计算判断哪艘船先到达． 【答案】（1）收到求救讯息时事故渔船 P 与救助船 B 之间的距离为 60 2 海里；（2）救助船 B 先到达． 【详解】 (1)如图，作 PC AB 于C ， 则 90PCA PCB     ， 由题意得： =120PA 海里， =30A  ， =45BPC  ， ∴ 1 602PC PA  海里， BCP 是等腰直角三角形， ∴ 60BC PC  海里， 2 2 60 2PB PC BC   海里， 答：收到求救讯息时事故渔船 P 与救助船 B 之间的距离为 60 2 海里； (2)∵ 120PA  海里， 60 2PB  海里，救助船 ,A B 分别以 40 海里/小时、30 海里/小时的速度同时出发， ∴救助船 A 所用的时间为 120 =340 (小时)， 救助船 B 所用的时间为 60 2 2 230  (小时)， ∵3 2 2 ， ∴救助船 B 先到达． 4．（2012·山东中考模拟）如图，某船以每小时 36 海里的速度向正东方向航行，在点 A 测得某岛 C 在北偏 东 60°方向上，航行半小时后到达点 B 测得该岛在北偏东 30°方向上，已知该岛周围 16 海里内有暗礁． （1）说明点 B 是否在暗礁区域内； （2）若继续向东航行有无触礁的危险？请说明理由． 【答案】（1）B 点不在暗礁区域内；（2）继续向东航行船有触礁的危险，理由见解析. 【解析】 （1）B 是否在暗礁区域内就要看 CB 的距离，若 CB＞16，则点 B 不在暗礁区域内；若 CB＜16，则点 B 在 暗礁区域内. （2）往东航行是否有触礁危险，就要看点 C 到 AB 的距离 CH 与 16 的大小关系.若 CH＞16，则无触礁的危 险；若 CB＜16，则有触礁的危险