九年级上册青岛版数学教案3-1圆的对称性 4页

- 1 - 3.1 圆的对称性 教学目标 【知识与能力】 (1)理解圆的轴对称性和中心对称性，会画出圆的对称轴，会找圆的对称中心； (2)掌握圆心角、弧和弦之间的关系，并会用它们之间的关系解题． 【过程与方法】 (1)通过对圆的对称性的理解，培养学生的观察、分析、发现问题和概括问题的能力，促进 学生创造性思维水平的发展和提高； (2)通过对圆心角、弧和弦之间的关系的探究，掌握解题的方法和技巧． 【情感态度价值观】 经过观察、总结和应用等数学活动，感受数学活动充满了探索性与创造性，体验发现的乐趣． 教学重难点 【教学重点】 对圆心角、弧和弦之间的关系的理解． 【教学难点】 能灵活运用圆的对称性解决有关实际问题，会用圆心角、弧和弦之间的关系解题． 课前准备 多媒体课件 教学过程 一、创设情境，导入新课 问：前面我们已探讨过轴对称图形，哪位同学能叙述一下轴对称图形的定义？ (如果一个图形沿着某一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做 轴对称图形，这条直线叫做对称轴)． 问：我们是用什么方法来研究轴对称图形？ 生：折叠． 今天我们继续来探究圆的对称性． 问题1：前面我们已经认识了圆，你还记得确定圆的两个元素吗？ 生：圆心和半径． 问题2：你还记得学习圆中的哪些概念吗？ 忆一忆： 1．圆：平面上到____________等于______的所有点组成的图形叫做圆，其中______为圆心， 定长为________． 2．弧：圆上_____叫做圆弧，简称弧，圆的任意一条____的两个端点分圆成两条弧，每一条 弧都叫做圆的半径．__________称为优弧，_____________称为劣弧． 3．___________叫做等圆，_________叫做等弧． 4．圆心角：顶点在_____的角叫做圆心角． 二、探究交流，获取新知 知识点一：圆的对称性 1．圆是轴对称图形吗？如果是，它的对称轴是什么？你能找到多少条对称轴？ - 2 - 2．大家交流一下：你是用什么方法来解决这个问题的呢？ 动手操作：请同学们用自己准备好的圆形纸张折叠：看折痕经不经过圆心？ 学生讨论得出结论：我们通过折叠的方法得到圆是轴对称图形，经过圆心的一条直线是圆的 对称轴，圆的对称轴有无数条． 知识点二：垂径定理 按下面的步骤做一做： 1．在一张纸上任意画一个⊙O，沿圆周将圆剪下，把这个圆对折，使圆的两半部分重合． 2．得到一条折痕 CD． 3．在⊙O上任取一点 A，过点 A 作 CD 折痕的垂线，得到新的折痕，其中，点 M 是两条折痕 的交点，即垂足． 4．将纸打开，新的折痕与圆交于另一点 B，如上图． 师：老师和大家一起动手． (教师叙述步骤，师生共同操作) 师：通过第一步，我们可以得到什么？ 学生齐声：可以知道：圆是轴对称图形，过圆心的直线是它的对称轴． 师：很好．在上述的操作过程中，你发现了哪些相等的线段和相等的弧？ 生：我发现了，AM=BM，  AC BC ，  AD BD ． 师：为什么呢？ 生：因为折痕 AM 与 BM 互相重合，A 点与 B 点重合． 师：还可以怎么说呢？能不能利用构造等腰三角形得出上面的等量关系？ 师生共析：如下图示，连接 OA、OB 得到等腰△OAB，即 OA=OB．因 CD⊥AB，故△OAM 与△OBM 都是 Rt△，又 OM 为公共边，所以两个直角三角形全等，则 AM=BM．又⊙O 关于直径 CD 对称， 所以 A 点和 B 点关于 CD 对称，当圆沿着直径 CD 对折时，点 A 与点 B 重合， AC 与 BC 重 合， AD 与 BD 重合．因此 AM=BM， AC = BC ， AD = BD ． 师：在上述操作过程中，你会得出什么结论？ 生：垂直于弦的直径平分这条弦，并且平分弦所对的弧． 结论：垂径定理：垂直于弦的直径平分弦以及弦所对的两条弧. 例1：如教材69页图3-4，以△OAB的顶点O为圆心的⊙O交AB于点C，D，且AC=BD.求证：OA=OB. 例2:1400多年前，我国隋唐时期建造的赵州石拱桥的桥拱近似于圆弧形，它的跨度为37.02m， 拱高(弧的中点到弦的距离，也叫弓形的高)为7.23m.求拱桥所在圆的半径(精确到0.1m). 知识点三：圆的中心对称性． 问：一个圆绕着它的圆心旋转任意一个角度，还能与原来的图形重合吗？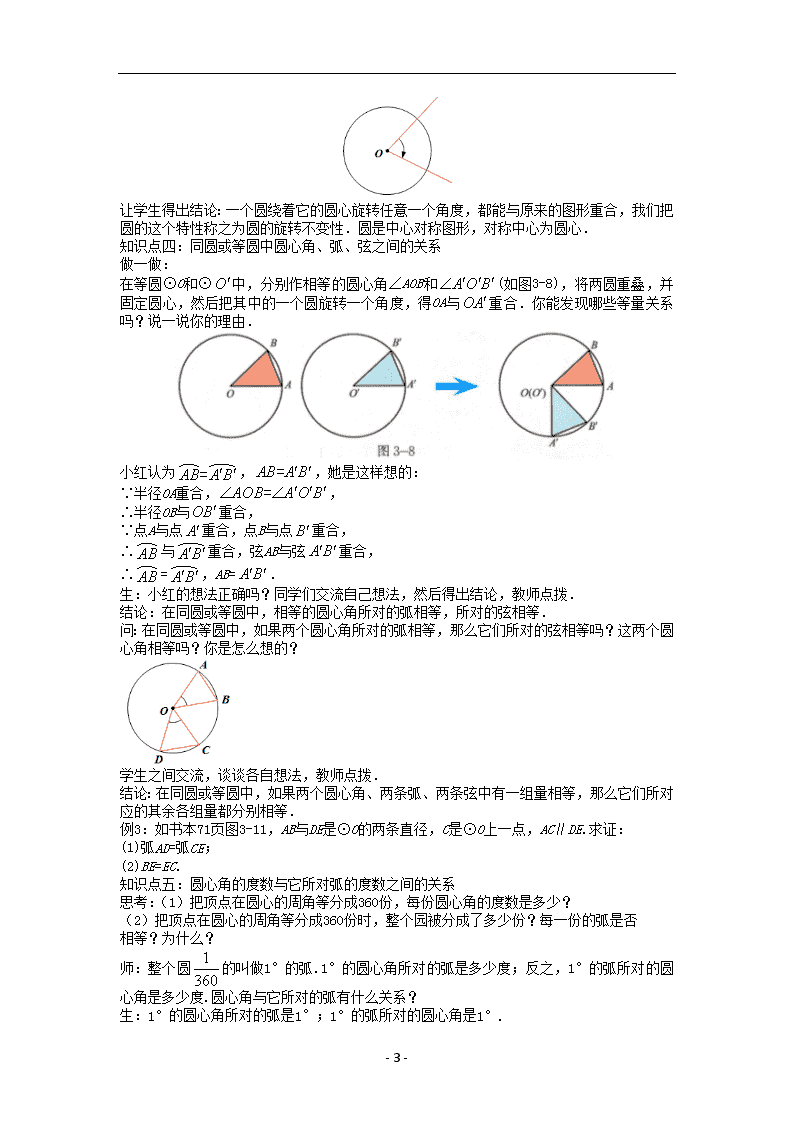 - 3 - 让学生得出结论：一个圆绕着它的圆心旋转任意一个角度，都能与原来的图形重合，我们把 圆的这个特性称之为圆的旋转不变性．圆是中心对称图形，对称中心为圆心． 知识点四：同圆或等圆中圆心角、弧、弦之间的关系 做一做： 在等圆⊙O和⊙ O 中，分别作相等的圆心角∠AOB和 A O B   (如图3-8)，将两圆重叠，并 固定圆心，然后把其中的一个圆旋转一个角度，得OA与 OA 重合．你能发现哪些等量关系 吗？说一说你的理由． 小红认为   =AB A B ，  =AB A B ，她是这样想的： ∵半径OA重合，    =AOB A O B ， ∴半径OB与OB重合， ∵点A与点 A重合，点B与点 B重合， ∴ AB 与 A B  重合，弦AB与弦 A B  重合， ∴ AB = A B  ，AB= A B  ． 生：小红的想法正确吗？同学们交流自己想法，然后得出结论，教师点拨． 结论：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等． 问：在同圆或等圆中，如果两个圆心角所对的弧相等，那么它们所对的弦相等吗？这两个圆 心角相等吗？你是怎么想的？ 学生之间交流，谈谈各自想法，教师点拨． 结论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对 应的其余各组量都分别相等． 例3：如书本71页图3-11，AB与DE是⊙O的两条直径，C是⊙O上一点，AC∥DE.求证： (1)弧AD=弧CE； (2)BE=EC. 知识点五：圆心角的度数与它所对弧的度数之间的关系 思考：（1）把顶点在圆心的周角等分成360份，每份圆心角的度数是多少？ （2）把顶点在圆心的周角等分成360份时，整个园被分成了多少份？每一份的弧是否 相等？为什么？ 师：整个圆 1 360 的叫做1°的弧.1°的圆心角所对的弧是多少度；反之，1°的弧所对的圆 心角是多少度.圆心角与它所对的弧有什么关系？ 生：1°的圆心角所对的弧是1°；1°的弧所对的圆心角是1°. - 4 - 结论：圆心角的度数与它所对弧的度数相等. 例4：如书本73页图3-14，OA，OC是⊙O中两条垂直的直径，D是⊙O上的一点.连接AD并延长 与OC的延长线相交于点B，∠B=25°.求弧AD，弧CD的度数. 例5：如书本73页图3-15，在⊙O中，弦AB所对的劣弧为圆的 3 1 ，圆的半径为2cm，求AB的长. 三、随堂练习 1．日常生活中的许多图案或现象都与圆的对称性有关，试举几例． 2．利用一个圆及其若干条弦分别设计出符合下列条件的图案： (1)是轴对称图形但不是中心对称图形； (2)是中心对称图形但不是轴对称图形； (3)既是轴对称图形又是中心对称图形． 3．已知，A，B是⊙O上的两点，∠AOB=120°，C是 AB 的中点，试确定四边形OACB的形状， 并说明理由． 四、自我小结，获取感悟 1．对自己说，你在本节课中学习了哪些知识点？有何收获？ 2．对同学说，你有哪些学习感悟和温馨提示？ 3．对老师说，你还有哪些困惑？