【精品】人教版 九年级下册数学 29 7页

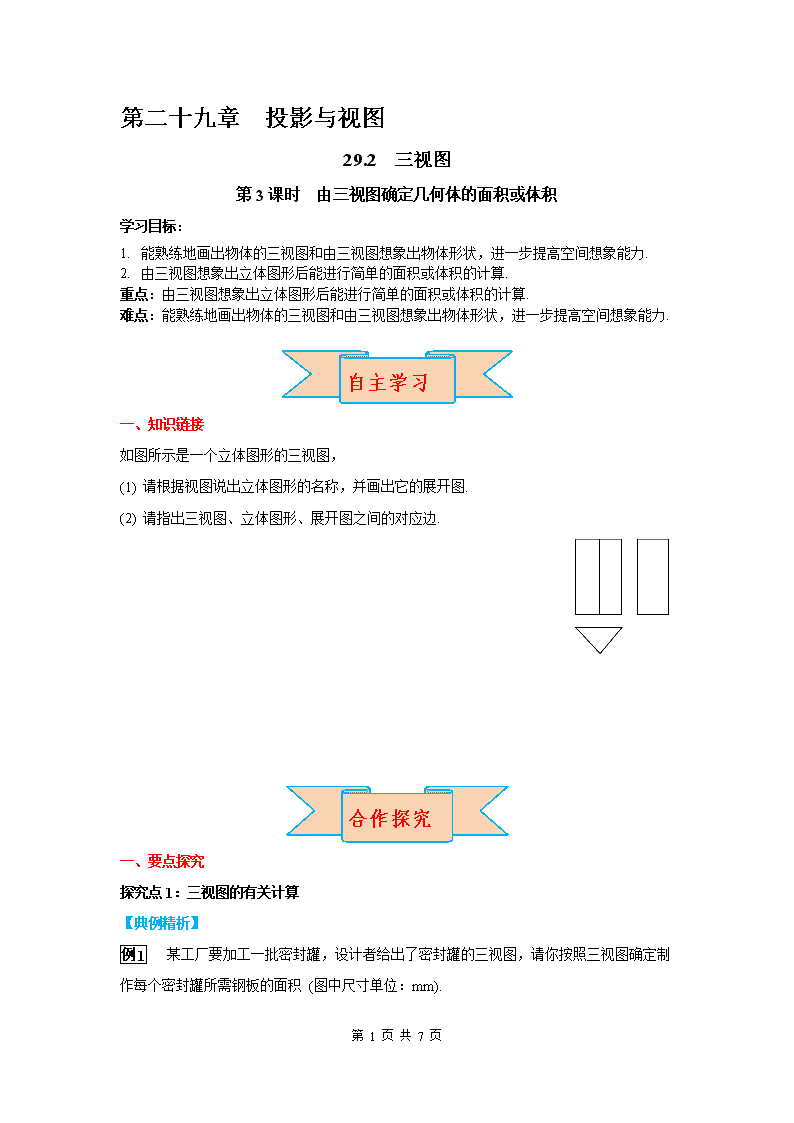
第 1 页 共 7 页 第二十九章 投影与视图 29.2 三视图 第 3 课时 由三视图确定几何体的面积或体积 学习目标： 1. 能熟练地画出物体的三视图和由三视图想象出物体形状，进一步提高空间想象能力. 2. 由三视图想象出立体图形后能进行简单的面积或体积的计算. 重点：由三视图想象出立体图形后能进行简单的面积或体积的计算. 难点：能熟练地画出物体的三视图和由三视图想象出物体形状，进一步提高空间想象能力. 自主学习 一、知识链接 如图所示是一个立体图形的三视图， (1) 请根据视图说出立体图形的名称，并画出它的展开图. (2) 请指出三视图、立体图形、展开图之间的对应边. 合作探究 一、要点探究 探究点 1：三视图的有关计算 【典例精析】 例 1 某工厂要加工一批密封罐，设计者给出了密封罐的三视图，请你按照三视图确定制 作每个密封罐所需钢板的面积 (图中尺寸单位：mm). 第 2 页 共 7 页 分析：1. 应先由三视图想象出密封罐的立体形状；2. 画出物体的展开图. 【归纳总结】 1. 三种图形的转化： 三视图 立体图 展开图 2. 由三视图求立体图形的面积的方法： (1) 先根据给出的三视图确定立体图形，并确定立体图形的长、宽、高. (2) 将立体图形展开成一个平面图形 (展开图)，观察它的组成部分. (3) 最后根据已知数据，求出展开图的面积. 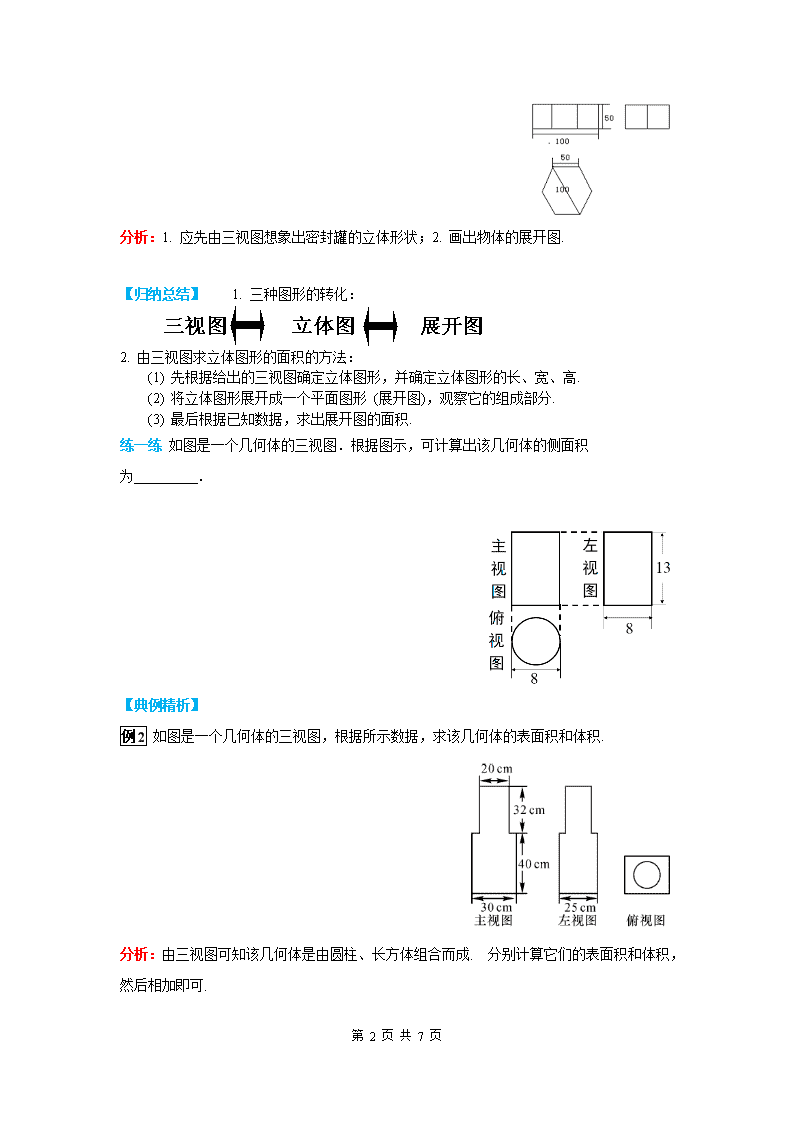练一练 如图是一个几何体的三视图．根据图示，可计算出该几何体的侧面积为 ． 【典例精析】 例 2 如图是一个几何体的三视图，根据所示数据，求该几何体的表面积和体积. 分析：由三视图可知该几何体是由圆柱、长方体组合而成. 分别计算它们的表面积和体积， 然后相加即可. 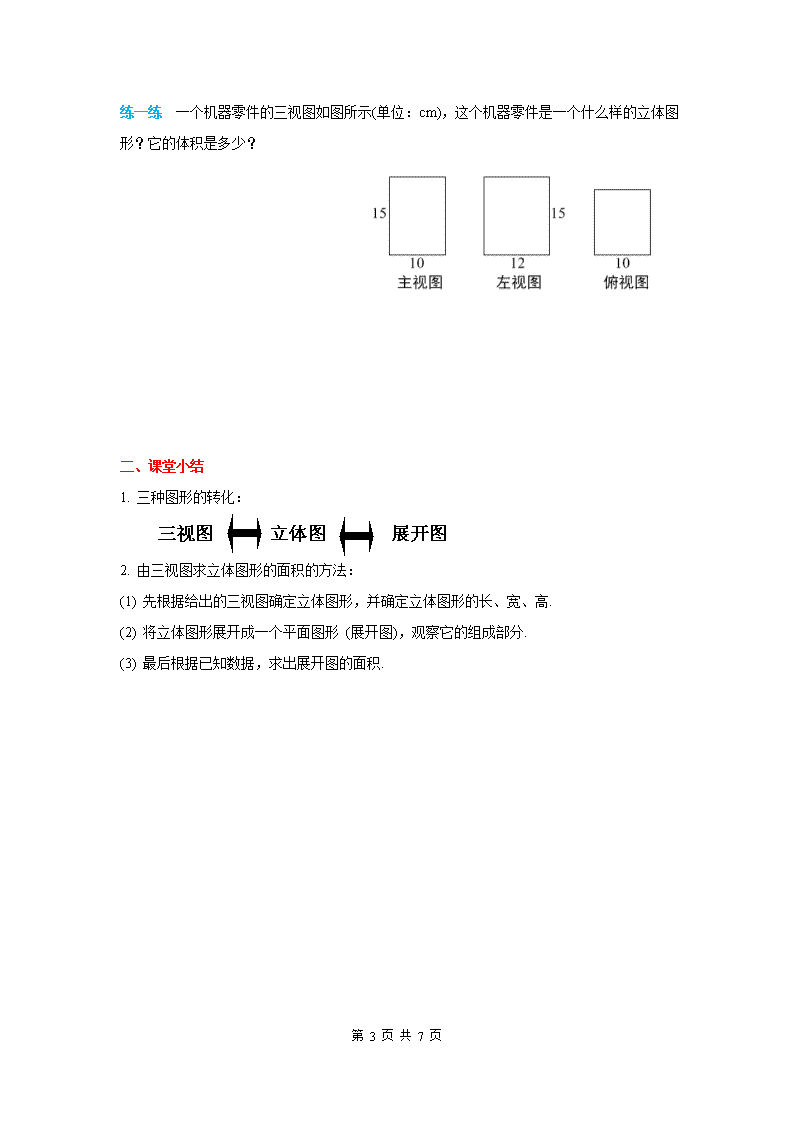练一练 一个机器零件的三视图如图所示(单位：cm)，这个机器零件是一个什么样的立体图 第 3 页 共 7 页 形？它的体积是多少？ 二、课堂小结 1. 三种图形的转化： 三视图 立体图 展开图 2. 由三视图求立体图形的面积的方法： (1) 先根据给出的三视图确定立体图形，并确定立体图形的长、宽、高. (2) 将立体图形展开成一个平面图形 (展开图)，观察它的组成部分. (3) 最后根据已知数据，求出展开图的面积. 当堂检测 1. 一个长方体的左视图、俯视图及相关数据如图所示，则其主视图的面积为 ( ) 第 4 页 共 7 页 A. 6 B. 8 C. 12 D. 24 2. 如图是一个几何体的三视图，根据图中提供的数据(单位：cm)，可求得这个几何体的体 积为 . 3. 如图是某几何体的三视图及相关数据(单位：cm)，则该几何体的侧面积为 cm2. 4. 如图是一个由若干个棱长为 1cm 的正方体构成的几何体的三视图． (1) 请写出构成这个几何体的正方体的个数为 ； (2) 计算这个几何体的表面积为 ． 5.如图是一个几何体的三视图，试描绘出这个零件的形状，并求出此三视图所描述的几何体 的表面积. 第 5 页 共 7 页 6.某一空间图形的三视图如图所示，其中主视图是半径为 1 的半圆以及高为 1 的矩形；左 视图是半径为 1 的四分之一圆以及高为 1 的矩形；俯视图是半径为 1 的圆，求此图形的体 积 (参考公式：V 球＝ 4 3 πR3)． 参考答案 自主学习 一、知识链接 （1）三棱柱 第 6 页 共 7 页 (2)略 合作探究 一、要点探究 探究点 1：三视图的有关计算 【典例精析】 例 1 解：由三视图可知，密封罐的形状是正六棱柱.密封罐的高为 50mm，底面正六边形的 直径为 100mm，边长为 50mm，如图，是它的展开图. 由展开图可知，制作一个密封罐所需钢板的面积为 16 50 50+2 6 50 50sin 602        2 236 50 1+ 27990(mm ).2         练一练 104π 【典例精析】 例 2 解：该图形上、下部分分别是圆柱、长方体，根据图中数据得：表面积为 20×32π+30×40×2+25×40×2+25×30×2=(5 900+640π)(cm2),体积为 25×30×40+10²×32π= (30 000+3 200π)(cm3). 练一练 解：长方体，其体积为 10×12×15=1800(cm3). 当堂检测 1. B 2. 3 cm3 3. 2π 4.（1）5 （2）20cm2 5.解：该几何体的表面积为π×2²+2π×2×2+ 2 1 ×4×4π=20 π. 6.解：由已知可得该几何体是一个下部为圆柱，上部为 1 4 球的组合体．由三视图可得，下部 第 7 页 共 7 页 圆柱的底面半径为 1，高为 1，则 V 圆柱＝π，上部 1 4 球的半径为 1，则 球 4 1V ＝ π 3 ，故此几何 体的体积为 4π 3 .