- 48.32 KB
- 2021-11-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
课 题:14.1.4 整式的乘法(三)
主设计人: 备课组长签字: 级部主任签字:
基础达标
1.多项式与多项式相乘,先用一个多项式的_________乘另一个多项式的每一项,再把所得
的积__________.
2.计算:(m-n)(p+q)=_________,(x+1)(x-1)=_____________.
3.如果(2x-1)(2-x)=ax2+bx+c,那么 a=_______,b=_______,c=_______.
4.我校操场原来的长是 2x 米,宽比长少 10 米,现在把操场的长与宽都增加了 5 米,则整
个操场面积增加__________.
5.下列计算正确的是( )
A.(x+y)(x+y)=x2+y2 B.(x+1)2=x2+2x+1
C.(x+2)(x-3)=x2+x-6 D.(x+1)(x-6)=x2-6
6.请你从以下选项中选择合适的 M,N,使等式 2( 3)x M x x n 成立,你的答案是
( )
A. 2, 6M x N B. 2, 6M x N
C. 4, 12M x N D. 4, 12M x N
7.小雨家种了一块梯形的菜地,菜地的上底长为 )43( mn 米,下底长为 )52( nm 厘米,
它的高为 )2( nm 厘米,求此梯形的面积.
8.计算:
(1)(x+1)(x-4); (2)(x-3y)(2x+3y); (3)(x+2)(x-3)-(x-3)(x+3);
(4)(m-2n)(-m-n); (5)(x3-2)(x3+3)-(x2)3+ x2·x;
(6)(xy-x)(xy-y)+xy(x+y); (7)(m+1)(m-1)(m-2)(m-4).
综合运用
9.若等式(x-5)(x-7)=x2-mx+35 成立,则 m 的值为 .
10.三个连续偶数,如果设中间的一个为 n,则它们的积为( )
A. 34n n B. 26 6n n C. 3n n D. 3 4n n
11.已知: 3
2a b , 1ab ,化简 ( 2)( 2)a b 的结果是 .
12.如果(x2+px+8)(x2-3x+q)乘积中不含 x2 项和 x3 项,则 p,q 的值 ( )
A.p=0,q=0 B.p=3,q=1 C.p=–3,q=–9 D.p=–3,q=1
13.将一多项式[(17x23x4)(ax2bxc)],除以(5x6)后,得商式为(2x1),余式为 0.求 abc=
( )
A.3 B.23 C.25 D.29
14.先化简 2 2 2( 1)( 2 3) ( 1)( 2) (2 1)( 1)a a a a a a a ,再把你喜欢的一个非零
数 a 的值代入求值.
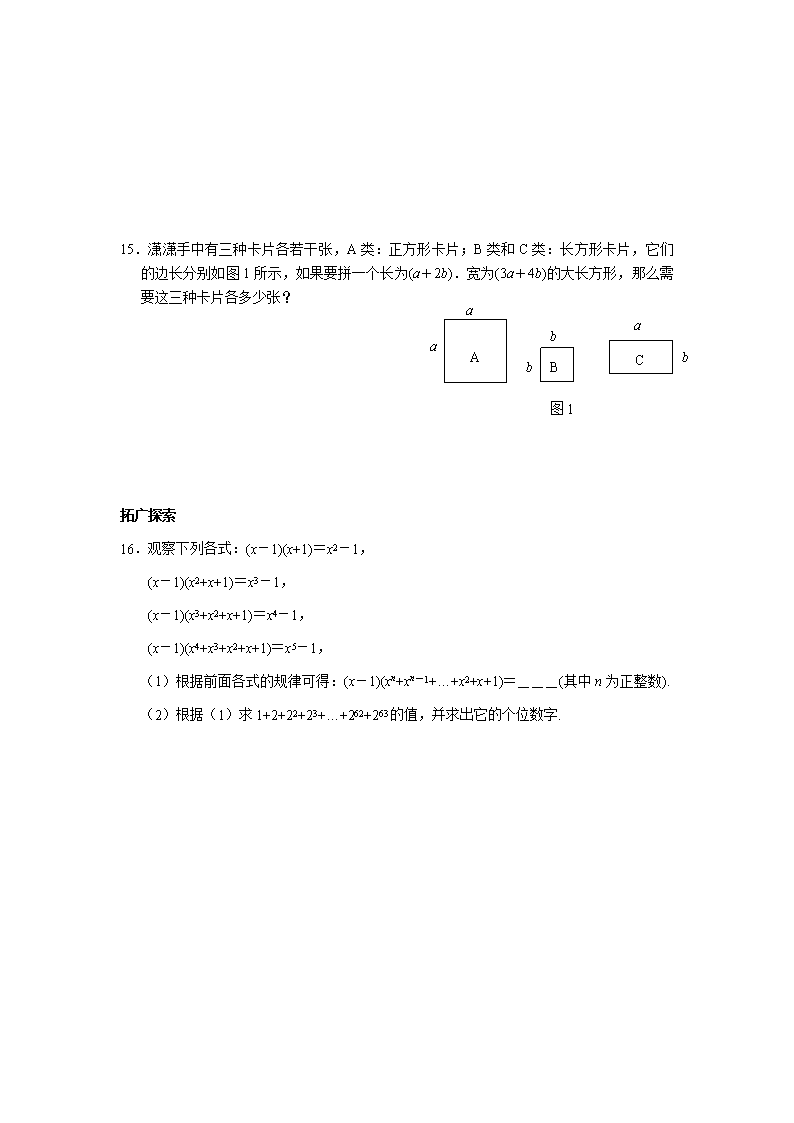
15.潇潇手中有三种卡片各若干张,A 类:正方形卡片;B 类和 C 类:长方形卡片,它们
的边长分别如图 1 所示,如果要拼一个长为(a+2b).宽为(3a+4b)的大长方形,那么需
要这三种卡片各多少张?
拓广探索
16.观察下列各式:(x-1)(x+1)=x2-1,
(x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1,
(x-1)(x4+x3+x2+x+1)=x5-1,
(1)根据前面各式的规律可得:(x-1)(xn+xn-1+…+x2+x+1)=___(其中 n 为正整数).
(2)根据(1)求 1+2+22+23+…+262+263 的值,并求出它的个位数字.
图 1
A B C
a
b
b
a
b
a
相关文档
- 人教版初中数学知识点总结-全面整2021-11-1034页
- 【初中数学干货】初中数学定理、公2021-11-1012页
- 沪科版(2012)初中数学八年级下册 172021-11-104页
- 【中考数学复习,PPT课件】初中数学2021-11-1053页
- 初中数学复习材料 A实数(综合)(初中初2021-11-1010页
- 初中数学苏科九上期中数学试卷2021-11-1010页
- 沪教版(上海)初中数学九年级第一学期2021-11-102页
- 初中数学竞赛辅导讲义及习题解答 2021-11-107页
- 初中数学竞赛辅导讲义及习题解答 2021-11-109页
- 初中数学阴影部分面积计算模型大全2021-11-109页