中考数学复习冲刺专项训练精讲：多边形与平行四边形教学课件（初三数学章节复习课件） 11页

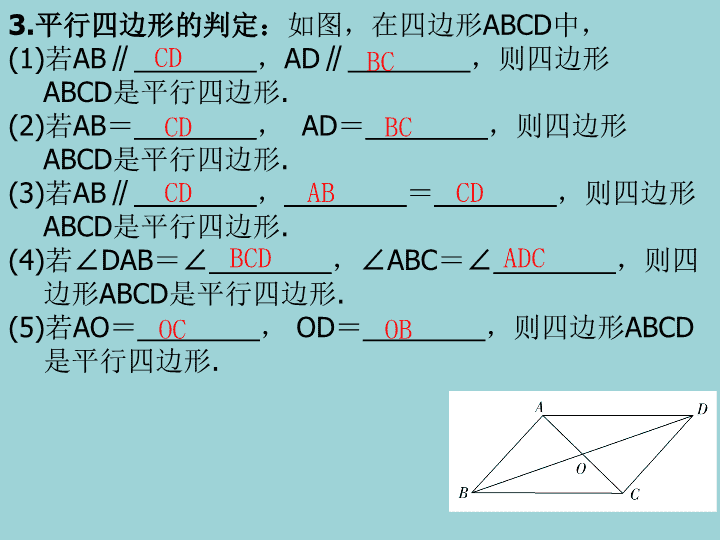
第五章　四边形 多边形与平行四边形 中考数学复习冲刺专项训练精讲 1.多边形的内角和外角： n边形内角和是__________，外角和是______. 一、考点知识 ， 2.平行四边形的性质：如图，在▱ ABCD中， (1)AB∥________，AD∥________； (2)AB＝________， AD＝________ . (3)∠DAB＝∠________，∠ABC＝∠________， ∠DAB ＋∠ABC ＝__________， ∠DAB ＋∠ADC＝__________. (4)AO＝________，OD＝________ . (5)▱ ABCD是________(填序号)．①轴对称图形，② 中心对称图形. (n-2)·180° 360° CD BC CD BC BCD ADC 180° 180° OC OB ② 3.平行四边形的判定：如图，在四边形ABCD中， (1)若AB∥________，AD∥________，则四边形 ABCD是平行四边形. (2)若AB＝________， AD＝________，则四边形 ABCD是平行四边形. (3)若AB∥________，________＝________，则四边形 ABCD是平行四边形. (4)若∠DAB＝∠________，∠ABC＝∠________，则四 边形ABCD是平行四边形. (5)若AO＝________， OD＝________，则四边形ABCD 是平行四边形. CD BC CD BC CD AB CD BCD ADC OC OB 【例1】若凸n边形的内角和为1 260°，求从一个顶 点出发引的对角线条数. 【考点1】多边形的内角和外角 二、例题与变式 解：六条 【变式1】如果正多边形的一个外角为36°，那么这个多 边形的边数有________ 条.10 【考点2】平行四边形的性质 【例2】如图，在▱ ABCD中，M，N是对角线BD 上的两点，BN＝DM，请判断AM与CN有怎样的关 系呢？并证明你的结论. 解：AM=CN，AM ∥CN. 证明:在△ABM与△CDN中, ∵BN=DM,又BM=BN－MN,DN=DM－MN. ∴BM=DN.① 又四边形ABCD是平行四边形,从而AB=CD,②∠ABM=∠CDM.③ 由①②③.得△ABM≌ △CDN(SAS) ∴AM=CN（全等三角形对应边相等）. 【变式2】如图，四边形ABCD是平行四边形，E， F是对角线BD上的点，∠1＝∠2. (1)求证：AE＝CF；(2)求证：AF∥CE. 解：证明：（1）∵四边形ABCD是平行四边形. ∴AB=CD，AB∥CD， ∴∠CDF=∠ABD. ∵∠1=∠2， ∴∠AEB=∠CFD. 在△ABE和△CDF中，∠AEB＝∠CFD,∠CDF=∠ABD,AB＝CD. ∴△ABE≌ △CDF（AAS）. ∴AE=CF. （2）由（1）,得△ABE≌ △CDF， ∴AE=CF， ∵∠1=∠2， ∴AE∥CF. ∴四边形AECF是平行四边形. ∴AF∥CE. 【考点3】平行四边形的判定 【例3】如图， A，E，F，C在同一直线上，已知BE∥DF， ∠ADF＝∠CBE，AF＝CE. 求证：四边形DEBF是平行四边形. 证明：∵BE∥DF，∴∠BEC=∠DFA. ∵在△ADF和△CBE中，∠BEC=∠DFA，∠ADF=∠CBE，AF=CE， ∴△ADF≌ △CBE（AAS）∴BE=DF. 又∵BE∥DF，∴四边形DEBF是平行四边形. 【变式3】如图，在△ABC中，D，E，F分别为边AB，BC，CA 的中点．求证：四边形DECF是平行四边形. 证明：∵D，F，E是△ABC各边的中点， ∴DF，DE是△ABC的中位线. ∴DF∥BC，DE∥AC. ∴四边形DECF是平行四边形. A组 1.六边形的内角和为______，外角和为__________. 三、过关训练 3.如图，在四边形ABCD中，∠A＋∠B＝180°，∠A＋∠D ＝180°. 求证：四边形ABCD是平行四边形. 2.一个平行四边形的一个外角是38°，这个平行四边形的内 角的度数分别是____________________ . 720° 360° 38°,142°,38°,142° 证明：∵∠A+∠B=180°，∠A+∠D=180°， ∴AD∥BC，AB∥DC. ∴四边形ABCD是平行四边形. B组 4.已知：如图，E，F分别是▱ ABCD的边AD，BC 的中点．求证：AF＝CE. 证明：∵四边形ABCD是平行四边形， 且E，F分别是AD，BC的中点，∴AE=CF. 又∵四边形ABCD是平行四边形， ∴AD∥BC，即AE∥CF. ∴四边形AFCE是平行四边形. ∴AF=CE. 解：过C作CE∥AB交AD于点E, ∵∠A+∠B=180°. ∴AD∥BC ∴∠D+∠C=180°. ∴∠D=30°. 又∵CE∥AB, ∴四边形ABCE是平行四边形. ∴AB=CE=8，AE=BC=6，∠BCE=∠A=120°. ∴∠DCE=150°－120°=30°=∠D. ∴CE=DE=6. ∴AD=AE+DE=8+6=14. 5．如图，在四边形ABCD中，AB＝8，BC＝6， ∠A＝120°，∠B＝60°，∠BCD＝150°，求AD 的长． C组 6．如图，在平行四边形ABCD中，∠C＝60°，M，N分别 是AD，BC的中点，BC＝2CD. (1)求证：四边形MNCD是平行四边形； (2)求证：BD＝ MN. 证明:（1）∵ABCD是平行四边形，∴AD=BC，AD∥BC， ∵M,N分别是AD,BC的中点，∴MD=NC.MD∥NC， ∴MNCD是平行四边形. （2）如题图，连接ND，∵MNCD是平行四边形，∴MN=DC． ∵N是BC的中点，∴BN=CN. ∵BC=2CD，∠C=60°，∴△NCD是等边三角形． ∴ND=NC，∠DNC=60°． ∵∠DNC是△BND的外角，∴∠NBD+∠NDB=∠DNC. ∵DN=NC=NB，∴∠DBN=∠BDN= ∠DNC=30°. ∴∠BDC=90°．∵tan∠BDC= ， ∴DB= DC= MN． 3 1 2 3 3 DC DB  3 3