九年级数学上册第一章特殊平行四边形2矩形的性质与判定第1课时矩形的性质作业课件新版北师大版 26页

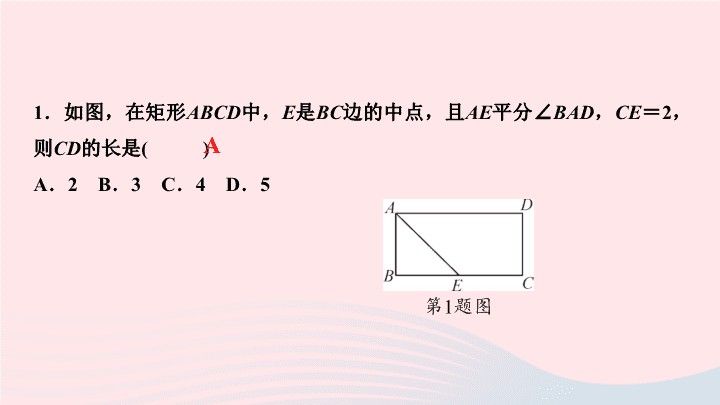
第一章　特殊平行四边形 1．2　矩形的性质与判定 第1课时　矩形的性质 1 ．如图，在矩形 ABCD 中， E 是 BC 边的中点，且 AE 平分∠ BAD ， CE ＝ 2 ，则 CD 的长是 ( ) A ． 2 B ． 3 C ． 4 D ． 5 A 2 ．如图，在矩形 ABCD 中， AB ＝ 2 BC ，在 CD 上取一点 E ，使 AE ＝ AB ，则∠ EBC 的度数是 ( ) A ． 30° B ． 22.5° C ． 15° D ． 10° C 3 ． (2019 · 福建 ) 如图，点 E ， F 分别是矩形 ABCD 的边 AB ， CD 上的一点，且 DF ＝ BE . 求证： AF ＝ CE . 4 ． (2019 · 十堰 ) 矩形具有而平行四边形不一定具有的性质是 ( ) A ．对边相等 B ．对角相等 C ．对角线相等 D ．对角线互相平分 C 5 ． ( 怀化中考 ) 如图，在矩形 ABCD 中，对角线 AC ， BD 相交于点 O ，∠ AOB ＝ 60° ， AC ＝ 6 cm ，则 AB 的长是 ( ) A ． 3 cm B ． 6 cm C ． 10 cm D ． 12 cm A 6 ． (2019 · 徐州 ) 如图，在矩形 ABCD 中， AC ， BD 相交于点 O ，点 M ， N 分别为 BC ， OC 的中点．若 MN ＝ 4 ，则 AC 的长为 ____ ． 16 7 ．如图，在矩形 ABCD 中，过点 B 作 BE ∥ AC 交 DA 的延长线于点 E . 求证： BE ＝ BD . 证明：∵四边形 ABCD 是矩形，∴ AC ＝ BD ， AD ∥ BC . 又∵ BE ∥ AC ，∴四边形 AEBC 是平行四边形，∴ BE ＝ AC ，∴ BE ＝ BD 8 ． ( 河南中考 ) 如图， BD 是矩形 ABCD 的一条对角线，点 E ， F 分别是 BD ， DC 的中点．若 AB ＝ 8 ， BC ＝ 6 ，则 AE ＋ EF 的长为 ( ) A ． 6 B ． 7 C ． 8 D ． 9 C 9 ． ( 锦州中考 ) 如图，菱形 ABCD 的对角线 AC ， BD 相交于点 O ，过点 A 作 AH ⊥ BC 于点 H ，连接 OH ，若 OB ＝ 4 ， S 菱形 ABCD ＝ 24 ，则 OH 的长为 ____ ． 3 10 ．如图，在 Rt△ ABC 中，∠ ACB ＝ 90° ， CD 是 AB 边上的中线，将△ ADC 沿 AC 边所在的直线翻折，使点 D 落在点 E 处，得到四边形 ABCE . 求证： EC ∥ AB . 解： ∵∠ ACB ＝ 90° ， CD 是 AB 边上的中线， ∴ CD ＝ AD ＝ DB ， ∴∠ CAD ＝ ∠ DCA . 又 ∵△ AEC 是由 △ ADC 翻折所得， ∴∠ ECA ＝ ∠ DCA ， ∴∠ ECA ＝ ∠ CAD ， ∴ EC ∥ AB 11 ． ( 遵义中考 ) 如图，点 P 是矩形 ABCD 的对角线 AC 上一点，过点 P 作 EF ∥ BC ，分别交 AB ， CD 于 E ， F ，连接 PB ， PD . 若 AE ＝ 2 ， PF ＝ 8. 则图中阴影部分的面积为 ( ) A ． 10 B ． 12 C ． 16 D ． 18 C A 15 ． (2019 · 大庆 ) 如图，在矩形 ABCD 中， AB ＝ 3 ， BC ＝ 4. M ， N 在对角线 AC 上，且 AM ＝ CN ， E ， F 分别是 AD ， BC 的中点． (1) 求证：△ ABM ≌△ CDN ； (2) 点 G 是对角线 AC 上的点，∠ EGF ＝ 90° ，求 AG 的长． 16 ．点 P 是矩形 ABCD 对角线 AC 所在直线上的一个动点 ( 点 P 不与点 A ， C 重合 ) ，分别过点 A ， C 向直线 BP 作垂线，垂足分别为点 E ， F ，点 O 为 AC 的中点 . (1) 如图①，当点 P 与点 O 重合时，请你判断 OE 与 OF 之间的数量关系； (2) 当点 P 运动到如图②所示的位置时，请你在图②中补全图形并通过证明判断 (1) 中的结论是否仍然成立． 解： (1) OE ＝ OF ，理由：∵四边形 ABCD 是矩形，∴ OA ＝ OC . 又∵ AE ⊥ BP ， CF ⊥ BP ，∴∠ AEO ＝∠ CFO ＝ 90°. 又∵∠ AOE ＝∠ COF ，∴△ AOE ≌△ COF (AAS) ，∴ OE ＝ OF