九年级上册青岛版数学课件2-4解直角三角形 25页

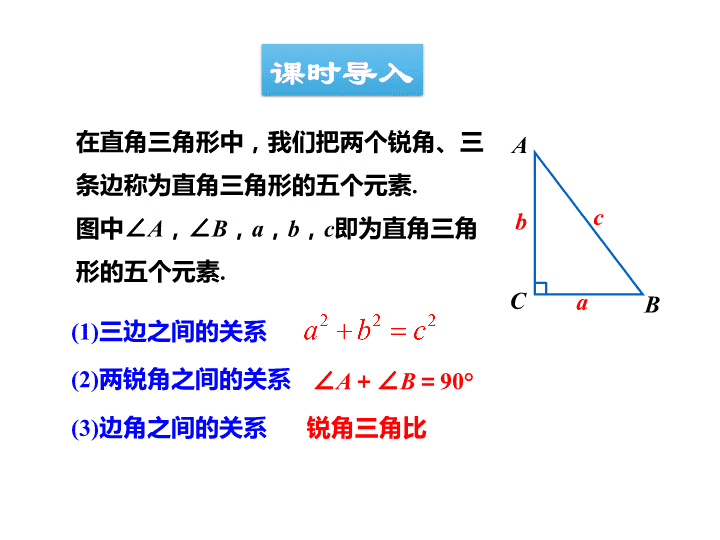
2.4解直角三角形 1.了解解直角三角形的含义. 2.经历解直角三角形的过程，掌握解直角三角形的方法. 学习目标 (2)两锐角之间的关系 ∠A＋∠B＝90° (3)边角之间的关系 (1)三边之间的关系 A Ba b c C 在直角三角形中，我们把两个锐角、三 条边称为直角三角形的五个元素. 图中∠A，∠B，a，b，c即为直角三角 形的五个元素. 锐角三角比 课时导入 A Ba b c C解直角三角形： 由直角三角形中已知元素求出未知元素的过程，叫作解 直角三角形． 一个直角三角形中，若已知五个 元素中的两个元素(其中必须有一个元 素是边)，则这样的直角三角形可解. 感悟新知 知道五个元素中的几个，就可以求其余元素？ 探究 必须已知除直角外的两个元素（至少有一个是边）. 已知两边：a.两直角边；b.一直角边和斜边. 已知一边和一锐角：a.一直角边和一锐角；b.斜边和一 锐角. 在Rt△ABC中，如果已知其中两边的长，你能求出 这个三角形的其他元 素吗？ 1 应用勾股定理求斜边， 应用角的正切值求出 一锐角，再利用直角 三角形的两锐角互余， 求出另一锐角．一般 不用正弦或余弦值求 锐角，因为斜边是一 个中间量，如果是近 似值，会影响结果的 精确度． 已知斜边和直角边： 先利用勾股定理求出 另一直角边，再求一 锐角的正弦和余弦值， 即可求出一锐角，再 利用直角三角形的两 锐角互余，求出另一 锐角． 已知两直角边： 已知斜边和直角边： 例1 如图，在 Rt△ABC 中，∠C=90°，AC= ，BC= 　 ，解这个直角三角形． 2 6 提问 需求的未知元素： 斜边AB、锐角A、锐角B. 方法一： 6tan = 3 2 60 =90 60 =30 =2 =2 2. BCA ,AC A B AB AC ∵ ∴∠ ， ∠ ，        方法二： 由勾股定理可得AB= .22. 3sin 60 90 30 2 ， BCA , A B A . AB           例2 已知在Rt△ABC中，∠C＝90°，∠A，∠B，∠C 的对边分别为a，b，c，且c＝5，b＝4，求这个三角 形的其他元素．(角度精确到1′) 求这个直角三角形的其他元素，与“解这个直角三角 形”的含义相同．求角时，可以先求∠A，也可以先 求∠B，因为 ＝sin B＝cos A. 导引： b c 由c＝5，b＝4，得sin B＝ ＝0.8， ∴∠B≈53°8′. ∴∠A＝90°－∠B≈36°52′. 由勾股定理得 解： 4 5 b c  2 2 2 25 4 3.a c b     已知直角三角形的一边和一锐角，解直角三角 形时，若已知一直角边a和一锐角A： ① ∠B=90 °- ∠ A；②c= 若已知斜边c和一个锐角A： ① ∠ B=90°- ∠ A； ②a=c·sin A ; ③b=c·cos A. . sin t ; an ab A a A ③ 2 例4 如图，在 Rt△ABC中，∠C=90°，∠B= 35°，b=20，解这个直角三角形（结果保留小数 点后一位）． 提问 需求的未知元素： 直角边a、斜边c、锐角A. =90 =90 35 55 tan 20 28 6tan tan35 sin 20 34 9sin sin35 A B . bB ,a ba . .B bB ,c bc . .B 解： ∵ ∴ ∵ ∴                还有别的 解法吗？ 在直角三角形的6个元素中，直角是已知元素，如果 再知道一条边和第三 个元素，那么这个三角形的所有元 素就都可以确定下来. 例5 在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分 别为a，b，c，且c＝100，∠A＝26°44′.求这个三角形 的其他元素．(长度精确到0.01) 已知∠A，可根据∠B＝90°－∠A得到∠B的大小．而 已知斜边，必然要用到正弦或余弦函数． ∵∠A＝26°44′，∠C＝90°， ∴∠B＝90°－26°44′＝63°16′. 由sin A＝ 得a＝c·sin A＝100·sin 26°44′≈44.98. 由cos A＝ 得b＝c·cos A＝100·cos 26°44′≈89.31.,b c 解： 导引： ,a c 例6 如图，在△ABC中，AB＝1，AC＝ sin B＝ 求BC的长． 要求的BC边不在直角 三角形中，已知条件中 有∠B的正弦值，作BC边上的高， 将∠B置于直角三角形 中，利用解直角三角形就可 解决问题． 2， 2 4 ， 导引： 3 如图，过点A作AD⊥BC于点D. ∵AB＝1，sin B＝ ∴AD＝AB·sin B＝1× ＝ ∴BD＝ CD＝ ∴BC＝ 解： 2 4 ， 2 4 2 . 4 2 2 2 2 2 141 , 4 4 AB AD             2 2 2 2 2 302 . 4 4 AC AD           30 14 30 14 . 4 4 4 CD BD      通过作垂线(高)，将斜三角形分割成两个直角三角 形，然后利用解直角三角形来解决边或角的问题，这种 “化斜为直”的思想很常见．在作垂线时，要结合已知 条件，充分利用已知条件，如本题若过B点作AC的垂线， 则∠B的正弦值就无法利用． 1.已知在Rt△ABC中，∠C=90°. （1）若a= ,b= ,则c= ； （2）若a=10，c= ，则∠B= ； （3）若b=35，∠A=45°，则a= ； （4）若c=20，∠A=60°，则a= . 4 3 2 3 10 2 45° 2 15 35 10 3 随堂练习 2.如图，在Rt△ABC中，∠BAC=90°，点D在BC边上， 且△ABD是等边三角形．若AB=2，求△ABC的周长. （结果保留根号） 解：∵△ABD是等边三角形，∴∠B=60°. 在Rt△ABC中，AB=2，∠B=60°, 2 4 tan 2 31cos 2 ABBC AC AB B . B      g， △ABC的周长为2+ +4=6+2 3 2 3. 3.在Rt△ABC中，∠C=90°，tanA= ，△ABC 的周长为45cm，CD是斜边AB上的高，求CD的长.（精 确到0.1 cm） 12 5 5x 12x 13x 解： 5 15 1245 (cm) sin = 5 12 13 2 13 xAC A . x x x      ， 5x 12x 13x 15 12sin 6 9 cm 2 13 CD AC A .    g ( ). 解 直 角 三 角 形 由直角三角形中已知的元素求出未知元 素的过程，叫作解直角三角形. 两边：两直角边或斜边、一直角边 一边一角：直角边、一锐角或斜边、一 锐角