苏科版江苏省九年级上学期期中联考数学试题（2020年苏教版九年级数学上册期中考试测试卷） 4页

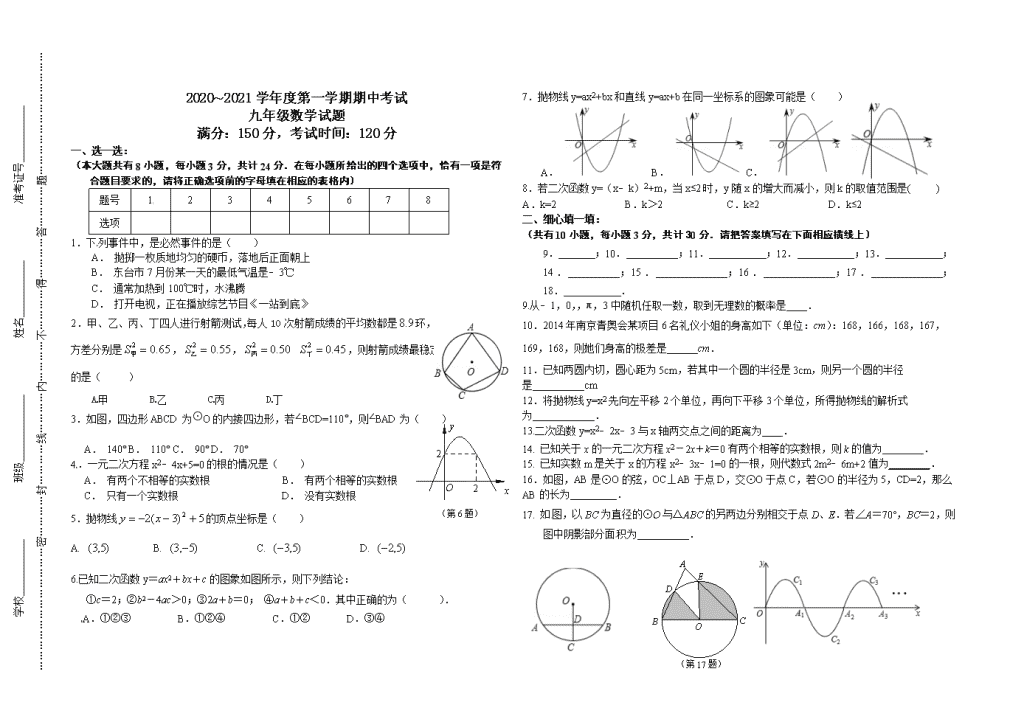
CB O A D E （第 17题） 2020～2021 学年度第一学期期中考试 九年级数学试题 满分：150 分，考试时间：120 分 一、选一选： （本大题共有 8 小题，每小题 3 分，共计 24 分．在每小题所给出的四个选项中，恰有一项是符 合题目要求的，请将正确选项前的字母填在相应的表格内．．．．．．） 题号 1] 2 3 4 5 6 7 8 选项 1．下列事件中，是必然事件的是（ ） A． 抛掷一枚质地均匀的硬币，落地后正面朝上 B． 东台市 7月份某一天的最低气温是﹣3℃ C． 通常加热到 100℃时，水沸腾 D． 打开电视，正在播放综艺节目《一站到底》 2．甲、乙、丙、丁四人进行射箭测试，每人 10 次射箭成绩的平均数都是8.9环， 方差分别是 2 0.65S 甲 ， 2 0.55S 乙 ， 2 0.50S 丙 2 0.45S 丁 ，则射箭成绩最稳 定的是（ ） A甲 B乙 C丙 D丁 3．如图，四边形 ABCD为⊙O的内接四边形，若∠BCD=110°，则∠BAD为（ ） A． 140° B． 110° C． 90° D． 70° 4．一元二次方程 x2﹣4x+5=0的根的情况是（ ） A． 有两个不相等的实数根 B． 有两个相等的实数根 C． 只有一个实数根 D． 没有实数根 5．抛物线 5)3(2 2  xy 的顶点坐标是（ ） A. )5,3( B. )5,3(  C. )5,3( D. )5,2( 6.已知二次函数 y＝ax2＋bx＋c的图象如图所示，则下列结论： ①c＝2；②b2－4ac＞0；③2a＋b＝0； ④a＋b＋c＜0．其中正确的为（ ）． A．①②③ B．①②④ C．①② D．③④ 7．抛物线 y=ax2+bx和直线 y=ax+b在同一坐标系的图象可能是（ ） A． B． C． 8．若二次函数 y=（x﹣k）2+m，当 x≤2时，y随 x的增大而减小，则 k的取值范围是( ) A．k=2 B．k＞2 C．k≥2 D．k≤2 二、细心填一填： （共有 10 小题，每小题 3 分，共计 30 分．请把答案填写在下面相．应横线．．．上．） 9． ；10． ；11． ；12． ；13． ； 14． ；15． ；16． ；17． ； 18． ． 9.从﹣1，0，，π，3中随机任取一数，取到无理数的概率是 ． 10．2014年南京青奥会某项目 6名礼仪小姐的身高如下（单位：cm）：168，166，168，167， 169，168，则她们身高的极差是 cm． 11．已知两圆内切，圆心距为 5cm，若其中一个圆的半径是 3cm，则另一个圆的半径 是 cm 12．将抛物线 y=x2先向左平移 2个单位，再向下平移 3个单位，所得抛物线的解析式 为 ． 13.二次函数 y=x2﹣2x﹣3与 x轴两交点之间的距离为 ． 14. 已知关于 x的一元二次方程 x2－2x＋k＝0有两个相等的实数根，则 k的值为 ． 15. 已知实数 m是关于 x的方程 x2﹣3x﹣1=0的一根，则代数式 2m2﹣6m+2值为________． 16．如图，AB是⊙O的弦，OC⊥AB于点 D，交⊙O于点 C，若⊙O的半径为 5，CD=2，那么 AB的长为 ． 17. 如图，以 BC为直径的⊙O与△ABC的另两边分别相交于点 D、E．若∠A＝70°，BC＝2，则 图中阴影部分面积为 ． 学 校 __ __ __ __ __ _ 班 级 __ __ __ __ __ __ _ 姓 名 __ __ __ __ __ _ 准 考 证 号 __ __ __ __ __ _ … … … … … … … … … … … … 密 … … … … 封 … … … … 线 … … … … 内 … … … … 不 … … … … 得 … … … … 答 … … … … 题 … … … … … … … … … … … … x y O 2 2 （第 6题） 18．如图，在平面直角坐标系 xOy 中，已知抛物线 y=﹣x（x﹣3）（0≤x≤3）在 x轴上方的部分， 记作 C1，它与 x轴交于点 O，A1，将 C1绕点 A1旋转 180°得 C2，C2与 x 轴交于另一点 A2．请继续 操作并探究：将 C2绕点 A2旋转180°得 C3，与 x 轴交于另一点 A3；将 C3绕点 A2旋转 180°得 C4， 与 x 轴交于另一点 A4，这样依次得到 x 轴上的点 A1，A2，A3，…，An，…，及抛物线 C1，C2，…， Cn，…则 Cn的顶点坐标为 （n为正整数，用含 n的代数式表示）． 三、用心做一做（本大题共有 10 小题，共 96 分．解答时应写出必要的文字说明、证明过程或演 算步骤） 19.（本题 8分）桌面上放有 4张卡片，正面分别标有数字 1，2，3，4．这些卡片除数字外完全 相同，把这些卡片反面朝上洗匀后放在桌面上，甲从中任意抽出一张，记下卡片上的数字后仍 反面朝上放回洗匀，乙也从中任意抽出一张，记下卡片上的数字，然后将这两数相加． （1）请用列表或画树状图的方法求两数之和为 5 的概率； （2）若甲与乙按上述方式做游戏，当两数之和为 5 时，甲胜；当两数之和不为 5 时，则乙胜．若 甲胜一次得 12 分，谁先达到 120 分为胜．那么乙胜一次得多少分，这个游戏对双方公平？ 20. （本题 8 分）某厂为了解工人在单位时间内加工同一种零件的技能水平，随机抽取了 50 名 工人加工的零件进行检测，统计出他们各自加工的合格品数是 1﹣8 这 8 个整数，现提供统计图 的部分信息如图，请解答下列问题： （1）根据统计图，求这 50 名工人加工出的合格品数的中位数； （2）写出这 50 名工人加工出的合格品数的众数的可能取值； （3）厂方认定，工人在单位时间内加工出的合格品数不低于 3件为技能合格，否则，将接受技 能再培训．已知该厂有同类工人 400名，请估计该厂将接受技能再培训的人数． 21. （本题 8 分）已知关于 x 的一元二次方程（a+1）x 2 ﹣x+a 2 ﹣3a﹣3=0 有一根是 1． （1）求 a的值；（2）求方程的另一根． 22. （本题 8分）为建设美丽家园，某企业逐年增加对环境保护的经费投入，2012年投入了 400 万元，预计到 2014年将投入 576万元. （1）求 2012年至 2014年该单位环保经费投入的年平均增长率； （2）该单位预计 2015年投入环保经费不低于 680万元，若继续保持前两年的年平均增长率， 该目标能否实现？请通过计算说明理由. 23. 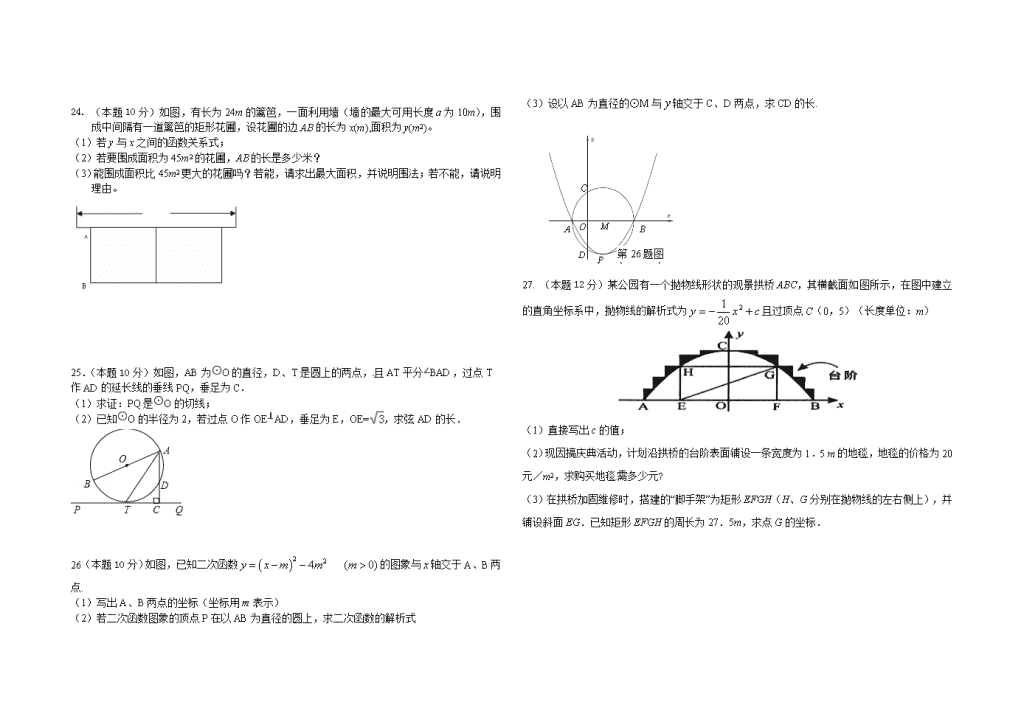（本题 10 分）如图，二次函数的图象与 x轴相交于 A（﹣3，0）、B（1，0）两点，与 y轴 相交于点 C（0，3），点 C、D是二次函数图象上的一对对称点，一次函数的图象过点 B、D． （1）求 D点坐标； （2）求二次函数的解析式； （3）根据图象直接写出使一次函数值小于二次函数值的 x的取 值范围． 24. （本题 10 分）如图，有长为 24m的篱笆，一面利用墙（墙的最大可用长度 a为 10m），围 成中间隔有一道篱笆的矩形花圃，设花圃的边 AB的长为 x(m),面积为 y(m2)。 （1）若 y与 x之间的函数关系式； （2）若要围成面积为 45m2的花圃，AB的长是多少米？ （3）能围成面积比 45m2更大的花圃吗？若能，请求出最大面积，并说明围法；若不能，请说明 理由。 25．（本题 10 分）如图，AB为⊙O的直径，D、T是圆上的两点，且 AT平分∠BAD，过点 T 作 AD的延长线的垂线 PQ，垂足为 C． （1）求证：PQ是⊙O的切线； （2）已知⊙O的半径为 2，若过点 O作 OE⊥AD，垂足为 E，OE= ，求弦 AD的长． 26（本题 10 分）如图，已知二次函数  2 24 ( 0)y x m m m    的图象与 x轴交于 A、B两 点. （1）写出 A、B两点的坐标（坐标用m表示） （2）若二次函数图象的顶点 P在以 AB为直径的圆上，求二次函数的解析式 （3）设以 AB为直径的⊙M与 y轴交于 C、D两点，求 CD的长. 27. （本题 12 分）某公园有一个抛物线形状的观景拱桥 ABC，其横截面如图所示，在图中建立 的直角坐标系中，抛物线的解析式为 cxy  2 20 1 且过顶点 C（0，5）（长度单位：m） （1）直接写出 c的值； （2）现因搞庆典活动，计划沿拱桥的台阶表面铺设一条宽度为 1．5 m的地毯，地毯的价格为 20元／m2，求购买地毯需多少元? （3）在拱桥加固维修时，搭建的“脚手架”为矩形 EFGH（H、G分别在抛物线的左右侧上），并 铺设斜面 EG．已知矩形 EFGH的周长为 27．5m，求点 G的坐标． A B C D O P M  24第 题图第 26题图 28．（本题 12 分）已知：抛物线 y=ax2+bx+c（a≠0）经过点 A（2，0），它的顶点坐标为 D（4， ﹣2），并与 x轴交于另一点 B，交 y轴于点 C． （1）求抛物线和直线 BC的函数表达式； （2）如图①，点 P是直线 BC下方抛物线上一动点，过点 P作 y轴的平行线，交直线 BC于点 E．是否存在一点 P，使线段 PE的长最大？若存在，求出 PE的最大值；若不存在，请说明理由； （3）如图②，过点 A作 y轴的平行线，交直线 BC于点 F，连接 DA、DB．四边形 OAFC 沿射线 CB方向运动，速度为每秒 1个单位长度，运动时间为 t秒，当点 C与点 B重合时立即停 止运动，设运动过程中四边形 OAFC与四边形 ADBF重叠部分面积为 S，请求出 S与 t的函数关 系式．