2021年中考数学压轴题专项训练 圆的综合（含解析） 23页

2021 年中考数学压轴题专项训练《圆的综合》 1．如图，四边形 ABCD 是⊙O 的内接四边形， ，AC 为直径，DE⊥BC，垂足为 E． （1）求证：CD 平分∠ACE； （2）若 AC＝8，CE＝3，求 CD 的长． （1）证明：∵四边形 ABCD 是⊙O 内接四边形， ∴∠BAD+∠BCD＝18 0°， ∵∠BCD+∠DCE＝180°， ∴∠DCE＝∠BAD， ∵ ， ∴∠BAD＝∠ACD， ∴∠DCE＝∠ACD， ∴CD 平分∠ACE； （2）解：∵AC 为直径， ∴∠AD C＝90°， ∵DE⊥BC， ∴∠DEC＝90°， ∴∠DEC＝∠ADC， ∵∠DCE＝∠ACD， ∴△DCE∽△ACD， ∴ ，即 ， ∴ ． 2．如图，AB 为⊙O 的直径，C、F 为⊙O 上两点，且点 C 为 的中点，过点 C 作 AF 的 垂线，交 AF 的延长线于点 E，交 AB 的延长线于点 D． （1）求证：DE 是⊙O 的切线； （2）当 BD＝2，sinD＝ 时，求 AE 的长． （1）证明：连接 OC，如图， ∵点 C 为弧 BF 的中点， ∴弧 BC＝弧 CF． ∴∠BAC＝∠FAC， ∵OA＝OC， ∴∠OCA＝∠OAC． ∴∠OCA＝∠FAC， ∴OC∥AE， ∵AE⊥DE， ∴OC⊥DE． ∴DE 是⊙O 的切线； （2）∵sinD＝ ＝ ， ∴设 OC＝3x，OD＝5x， 则 5x＝3x+2， ∴x＝1， ∴OC＝3，OD＝5， ∴AD＝8， ∵sinD＝ ＝ ＝ ， ∴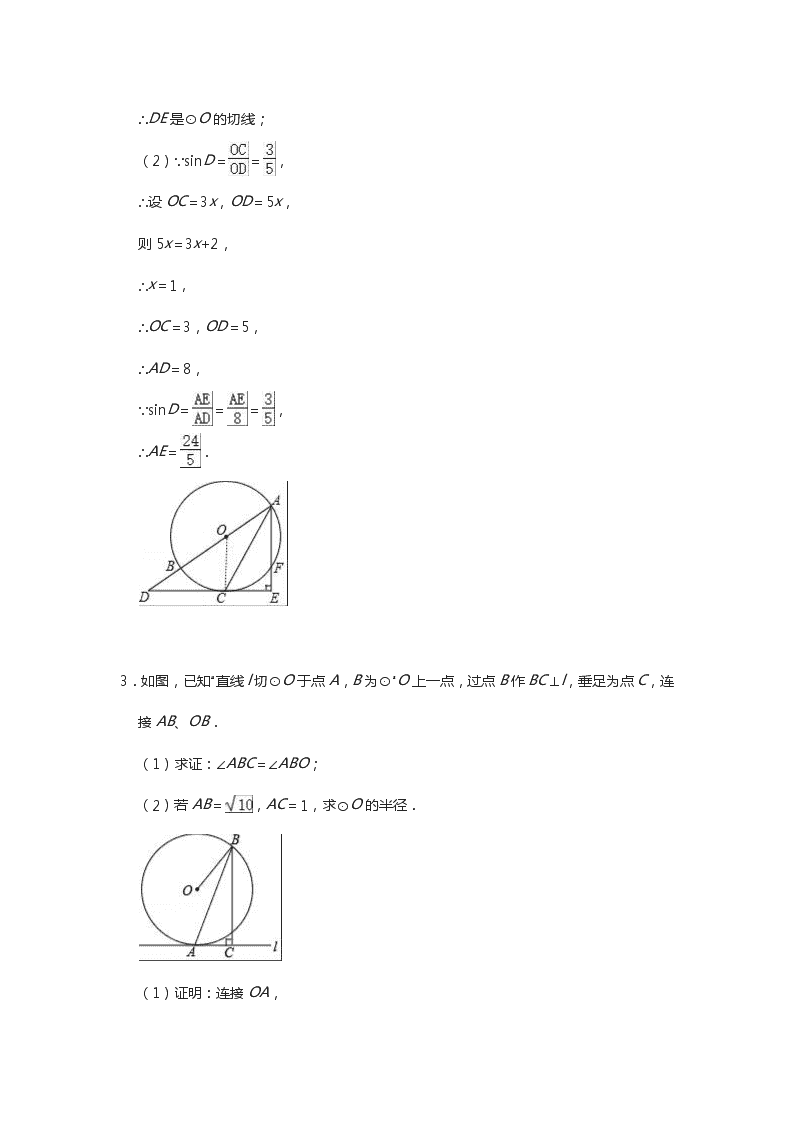AE＝ ． 3．如图，已知 直线 l 切⊙O 于点 A，B 为⊙ O 上一点，过点 B 作 BC⊥l，垂足为点 C，连 接 AB、OB． （1）求证：∠ABC＝∠ABO； （2）若 AB＝ ，AC＝1，求⊙O 的半径． （1）证明：连接 OA， ∵OB＝OA， ∴∠OBA＝∠OAB， ∵AC 切⊙O 于 A， ∴OA⊥AC， ∵BC⊥AC， ∴OA∥BC， ∴∠OBA＝∠ABC， ∴∠ABC＝∠ABO； （2）解：过 O 作 OD⊥BC 于 D， ∵OD⊥BC，BC⊥AC，OA⊥AC， ∴∠ODC＝∠DCA＝∠OAC＝90°， ∴OD＝AC＝1， 在 Rt△ACB 中，AB＝ ，AC＝1，由勾股定理得：BC＝ ＝3， ∵OD⊥BC，OD 过 O， ∴BD＝DC＝ BC＝ ＝1.5， 在 Rt△ODB 中，由勾股定理得：OB＝ ＝ ， 即⊙O 的半径是 ． 4．如图，AB 为⊙O 的直径，C 为⊙O 上一点，经过点 C 的切线交 AB 的延长线于点 E， AD⊥EC 交 EC 的延长线于点 D，连接 AC． （1）求证：AC 平分∠DAE； （2）若 cos∠DAE＝ ，BE＝2，求⊙O 的半径． （1）证明：连接 OC， ∵DE 是⊙O 的切线， ∴OC⊥DE， ∵AD⊥DE， ∴OC∥AD， ∴∠OCA＝∠DAC， ∵OA＝OC， ∴∠OCA＝∠OAC， ∴∠DAC＝∠OAC， ∴AC 平分∠DAE； （2）解：设⊙O 的半径为 r， ∵OC∥AD， ∴∠DAE＝∠COE， ∴cos∠DAE＝cos∠COE＝ ，BE＝2， ∴ ＝ ， 解得：r＝4， 即⊙O 的半径为 4． 5．如图 a，AB 为⊙O 直径，AC 为⊙O 的为弦，PA 为⊙O 的切线，∠APC＝2∠1． （1）求证：PC 是⊙O 的切线． （2）当∠1＝30°，AB＝4 时，其他条件不变，求图 b 中阴影部分的面积． （1）证明：连结 OC， 在圆 O 中，OA＝OC， ∴∠BOC＝2∠1＝∠APC，∠BOC+∠AOC＝180°， ∴∠APC+∠AOC＝180°， ∵PA 为⊙O 的切线， ∴∠OAP＝90° 又四边形内角和为 360°， ∴∠OCP＝90°，OC 为⊙O 的半径， ∴PC 为⊙O 的切线； （2）解：PA 为⊙O 的切线，PC 为⊙O 的切线． ∴PA＝PC， ∵∠1＝30°，∠APC＝2∠1， ∴∠APC＝60°， ∴△APC 为等边三角形， 连结 OP，OC， ∵S 四边形 AOCP＝2× ×2×2＝4，S 扇形 AOC＝×π×4＝π， ∴S 阴影部分的面积＝4﹣π． 6．如图，线段 AB 经过⊙O 的圆心，交⊙O 于 A，C 两点，BC＝1，AD 为⊙O 的弦，连 接 BD，∠BAD＝∠ABD＝30°，连接 DO 并延长交⊙O 于点 E，连接 BE 交⊙O 于点 M． （1）求证：直线 BD 是⊙O 的切线； （2）求切线 BD 的长； （3）求线段 BM 的长． （1）证明：∵∠BAD＝∠ABD＝30°， ∴∠DOB＝2∠BAD＝60°， ∴∠ODB＝180°﹣30°﹣60°＝90°， 即 OD⊥BD， ∵OD 过 O， ∴直线 BD 是⊙O 的切线； （2）解：设 OD＝OC＝r， 在 Rt△BDO 中，sin30°＝ ＝ ， 解得：r＝1， 即 OD＝1，OB＝1+1＝2， 由勾股定理得：BD＝ ＝ ； （3）解：连接 DM， ∵DE 是⊙O 的直径， ∴∠DME＝90°， 即∠DMB＝∠BDE＝90°， ∵∠DBM＝∠DBE， ∴△BMD∽△BDE， ∴ ， ∴ ， 解得：BM＝ ． 7．如图，四边形 ABCD 为⊙O 的内接四边形，且 AC 为⊙O 的直径， ＝ ，延长 BC 到 E，使得 BE＝AB，连接 DE． （1）求证：AD＝DE； （2）若 DE 为⊙O 的切线，且 DE＝2 ，求 的长度． （1）证明：连接 BD， ∵ ＝ ， ∴∠ABD＝∠DBE， ∵AB＝BE，BD＝BD， ∴△ABD≌△EBD（SAS）， ∴AD＝DE； （2）解：连接 OD， ∵ ＝ ， ∴AD＝CD， ∵AD＝DE， ∴CD＝DE， ∵AC 为⊙O 的直径， ∴∠B＝∠ADC＝90°， ∵AD＝CD，O 为 AC 的中点， ∴∠ODE＝ ∠ADC＝45°， ∵DE 为⊙O 的切线， ∴∠ODE＝90， ∴∠CDE＝45°， ∴∠ADE＝90°+45°＝135°， ∵CD＝DE， ∴∠DCE＝∠DEC＝67.5°， ∴∠BAD＝67.5°， ∵AD＝CD，∠ADC＝90°， ∴∠DAC＝45°， ∴∠BAC＝22.5°， ∴AD＝CD＝2 ， ∴AC＝4， ∴OC＝2， ∴ 的长度是 ＝ ． 8．如图，⊙O 是△ABC 的外接圆，AB 是直径，OD⊥AC，垂足为 D 点，直线 OD 与⊙O 相交于 E，F 两点，P 是⊙O 外一点，P 在直线 OD 上，连接 PA，PB，PC，且满足∠PCA ＝∠ABC （1）求证：PA＝PC； （2）求证：PA 是⊙O 的切线； （3）若 BC＝8， ，求 DE 的长． （1）证明∵OD⊥AC， ∴AD＝CD， ∴PD 是 AC 的垂直平分线， ∴PA＝PC， （2）证明：由（1）知：PA＝PC， ∴∠PAC＝∠PCA． ∵AB 是⊙O 的直径， ∴∠ACB＝90°， ∴∠CAB+∠CBA＝90°． 又∵∠PCA＝∠ABC， ∴∠PCA+∠CAB＝90°， ∴∠CAB+∠PAC＝90°，即 AB⊥PA， ∴PA 是⊙O 的切线； （3）解：∵AD＝CD，OA＝OB， ∴OD∥BC，OD＝ BC＝ ＝4， ∵ ＝ ， 设 AB＝3a，DF＝2a， ∵AB＝EF， ∴DE＝3a﹣2a＝a， ∴OD＝4＝ ﹣a， a＝8， ∴DE＝8． 9．如图，C 是 上的一定点，D 是弦 AB 上的一定点，P 是弦 CB 上的一动点，连接 DP， 将线段 PD 绕点 P 顺时针旋转 90°得到线段 PD′，射线 PD′与 交于点 Q．已知 BC＝6cm，设 P，C 两点间的距离为 xcm，P，D 两点间的距离为 y1cm，P，Q 两点间 的距离为 y2cm． 小石根据学习函数的经验，分别对函数 y1，y2 随自变量 x 的变化而变化的规律进行了探 究，下面是小石的探究过程，请补充完整： （1）按照下表中自变量 x 的值进行取点、画图、测量，分别得到了 y1，y2 与 x 的几组对 应值： x/cm 0 1 2 3 4 5 6 y1/cm 4.29 3.33 1.65 1.22 1.50 2.24 y2/cm 0.88 2.84 3.57 4.04 4.17 3.20 0.98 （2）在同一平面直角坐标系 xOy 中，描出补全后的表中各组数据所对应的点（x，y1）， （x，y2），并画出函数 y1，y2 的图象； （3）结合函数图象，解决问题：连接 DQ，当△DPQ 为等腰三角形时，PC 的长度约为 1.3 或 5.7 cm．（结果保留一位小数） 解：（1）观察图象发现规律可知： 表格数据为：2.44； （2）如图所示： 即为两个函数 y1，y2 的图象； （3）观察图象可知： 两个图象的交点的横坐标即为△DPQ 为等腰三角形时，PC 的长度， 两个交点的横坐标为 1.3 和 5.7． 故答案为：1.3 或 5.7． 10．如图（1），某数学活动小组经探究发现：在⊙O 中，直径 AB 与弦 CD 相交于点 P，此 时 PA•PB＝PC•PD （1）如图（2），若 AB 与 CD 相交于圆外一点 P，上面的结论是否成立？请说明理由． （2）如图（3），将 PD 绕点 P 逆时针旋转至与⊙O 相切于点 C，直接写出 PA、PB、PC 之间的数量关系． （3）如图（3），直接利用（2）的结论，求当 PC＝ ，PA＝1 时，阴影部分的面 积． 解：（1）成立．理由如下： 如图（2），连接 AD、BC， 则∠B＝∠D ∵∠P＝∠P ∴△PAD∽△PCB ∴ ＝ ∴PA•PB＝PC•PD； （2）PC2＝PA•PB 理由如下： 如图（3），连接 BC，OC， ∵PC 与⊙O 相切于点 C， ∴∠PCO＝90°， ∵AB 是直径， ∴∠ACB＝90° ∴∠PCA＝∠OCB ∵OC＝OB ∴∠OCB＝∠OBC ∴∠PCA＝∠OBC ∵∠P＝∠P ∴△PCA∽△PBC ∴PC：PB＝PA：PC ∴PC2＝PA•PB． （3）如图（3），连接 OC， ∵PC2＝PA•PB，PC＝ ，PA＝1 ∴PB＝3，AO＝CO＝1 ∴PO＝2 ∵PC 与⊙O 相切于点 C， ∴△PCO 是直角三角形 ∴sin∠CPO＝ ＝ ∴∠CPO＝30°，∠COP＝60° ∴△AOC 为等边三角形 ∴S△AOC＝ ＝ S 扇形 AOC＝ ＝ ∴S 阴影＝S 扇形 AOC﹣S△AOC ＝ ﹣ ． 11．在平面直角坐标系 xOy 中，已知点 A（0，2），点 B 在 x 轴上，以 AB 为直径作⊙C， 点 P 在 y 轴上，且在点 A 上方，过点 P 作⊙C 的切线 PQ，Q 为切点，如果点 Q 在第一 象限，则称 Q 为点 P 的离点．例如，图 1 中的 Q 为点 P 的一个离点． （1）已知点 P（0，3），Q 为 P 的离点． ①如图 2，若 B（0，0），则圆心 C 的坐标为 （0，1） ，线段 PQ 的长为 ； ②若 B（2，0），求线段 PQ 的长； （2）已知 1≤PA≤2，直线 l： y＝kx+k+3（k≠0）． ①当 k＝1 时，若直线 l 上存在 P 的离点 Q，则点 Q 纵坐标 t 的最大值为 6 ； ②记直线 l：y＝kx+k+3（k≠0）在﹣1≤x≤1 的部分为图形 G，如果图形 G 上存在 P 的离点，直接写出 k 的取值范围． 解：（1）①如图可知：C（0，1）， 在 Rt△PQC 中，CQ＝1，PC＝2， ∴PQ＝ ， 故答案为（0，1）； ； ②如图，过 C 作 CM⊥y 轴于点 M，连接 CP，CQ． ∵A（0，2），B（2，0）， ∴C（1，1）． ∴M（0，1）． 在 Rt△ACM 中，由勾股定理可得 CA＝ ． ∴CQ＝ ． ∵P（0，3），M（0，1）， ∴PM＝2． 在 Rt△PCM 中，由勾股定理可得 PC＝ ． 在 Rt△PCQ 中，由勾股定理可得 PQ＝ ＝ ． （2）①如图 1：当 k＝1 时，y＝x+4， ∴Q（t﹣2，t）， ∴CQ＝ ， 当 t＝2 时，CQ 最大， 在 Rt△CDQ 中，CD＝ ，CQ 最大则 DQ 最大， ∴Q（2，6）， 故答案为 6； ②∵﹣1≤x≤1， Q 点的在端点（﹣1，3）和（1，2k+4）之间运动， 当 Q 在（1，2k+4），P（0，4）时， 直线 PQ 的解析式 y＝（2k﹣1）x+4， 点 C（1，1）到直线 PQ 的距离为 时，可得 k＝0 或 k＝4， ∴0＜k＜4． 12．已知 AB 为⊙O 的直径． （1）如图 a，点 D 为 的中点，当弦 BD＝AC 时，求∠A． （2）如图 b，点 D 为 的中点，当 AB＝6，点 E 为 BD 的中点时，求 OE 的长． （3）如图 c，点 D 为 上任意一点（不与 A、C 重合），若点 C 为的中点，探求 BD、 AD、CD 之间的数量关系，直接写出你探求的结论，不要求证明． 解：（1）如图 1，连结 OC， 点 D 为 的中点， ∴ ＝ ═ ， ∵弦 BD＝AC， ∴ ＝ ， ∴ ═ ＝ ，即点 C 为 的中点． ∴ ＝ ═ ∠A＝ ∠COB＝ × ×180°＝30°． （2）如图 2，连结 OD，BC，OD 交 AC 于点 F， AB 为⊙O 的直径， ∴∠C＝90o 点 D 为 的中点，半径 OD 所在的直线为⊙O 的对称轴， 则点 A 的对应点为 C， ∴OD⊥AC，OD 平分 AC，即：AF＝CF， 在△DEF 和△BEC 中， ， ∴△DEF≌△BEC （AAS）， ∴CE＝EF，BC＝DF， ∵AO＝BO，AF＝CF， ∴OF＝ BC＝ DF，又 AB＝6， ∴OD＝3 ∴OF＝1，BC＝DF＝2． 在 Rt△ABC 中，AB＝6，BC＝2， ∴AC＝ ＝ ＝4 ， ∵点 F 为 AC 的中点，点 E 为 FC 的中点 ∴EF＝ ， 在 Rt△OFE 中，EF＝ ，OF＝1， ∴OE＝ ＝ ＝ ． （3）BD、AD、CD 之间的关系为：BD﹣AD＝ CD， 如图 3，连接 BC，OC， ∵AB 为⊙O 的直径，点 C 为 的中点， ∴∠ACB＝90°，AC＝BC， ∴∠BAC＝∠BDC＝45°， 过点 C 作 CF⊥CD 交 BD 于点 F， ∴△DCF 是等腰直角三角形， ∴ ， ∵∠ACD＝∠BCF＝90°﹣∠ACF， 又∵AC＝BC，CD＝CF ∴△ACD≌△BCF（SAS） ， ∴AD＝BF， ∵BD＝BF+DF， ∴BD＝AD+ CD， 即 BD﹣AD＝ CD． 13．如图，在△ABC 中，AB＝AC，∠A＝30°，AB＝10，以 AB 为直径的⊙O 交 BC 于 点 D，交 AC 于点 E，连接 DE，过点 B 作 BP 平行于 DE，交⊙O 于点 P，连接 CP、OP． （1）求证：点 D 为 BC 的中点； （2）求 AP 的长度； （3）求证：CP 是⊙O 的切线． 解：（1）BD＝DC．理由如下： 如图 1，连接 AD， ∵AB 是直径， ∴∠ADB＝90°， ∴AD⊥BC． （2）如图 1，连接 AP． ∵AD 是等腰△ABC 底边上的中线， ∴∠BAD＝∠CAD， ∴ ＝ ， ∴BD＝DE． ∴BD＝DE＝DC， ∴∠DEC＝∠DCE， △ABC 中，AB＝AC，∠A＝30°， ∴∠DCE＝∠ABC＝ （180°﹣30°）＝75°， ∴∠DEC＝75°， ∴∠EDC＝180°﹣75°﹣75°＝30°， ∵BP∥DE， ∴∠PBC＝∠EDC＝30°， ∴∠ABP＝∠ABC﹣∠PBC＝75°﹣30°＝45°， ∵OB＝OP， ∴∠OBP＝∠OPB＝45°， ∴∠BOP＝90°． ∴△AOP 是等腰直角三角形． ∵AO＝ AB＝5． ∴AP＝ AO＝5 ； （3）解法一：设 OP 交 AC 于点 G，如图 1，则∠AOG＝∠BOP＝90°， 在 Rt△AOG 中，∠OAG＝30°， ∴ ＝ ， 又∵ ＝ ＝ ， ∴ ＝ ， ∴ ＝ ． 又∵∠AGO＝∠CGP， ∴△AOG∽△CPG， ∴∠GPC＝∠AOG＝90°， ∴OP⊥PC， ∴CP 是⊙O 的切线； 解法二：如图 2，作 CM⊥AB 于 M， ∵∠BOP＝90°， ∴CM∥OP， ∵OP＝ AB， 在 Rt△AME 中， ∵∠BAC＝30°，可 ∴CM＝ AC， ∴CM＝ AB， ∴CM＝OP， ∴四边形 OPCM 是矩形， ∴∠CPO＝90°， ∴CP 是圆 O 的切线． 14．如图，⊙O 的半径为 ，AB 是⊙O 的直径，F 是⊙O 上一点，连接 FO、FB．C 为 劣弧 的中点，过点 C 作 CD⊥AB，垂足为 D，CD 交 FB 于点 E，CG∥FB，交 AB 的 延长线于点 G． （1）求证：CG 是⊙O 的切线； （2）连接 BC，若 BC∥OF，如图 2． ①求 CE 的长； ②图中阴影部分的面积等于 2π ． （1）证明：如图 1，连接 CO． ∵C 是 的中点， ∴∠BOC＝∠FOC． 又∵OF＝OB， ∴OC⊥BF． ∵CG∥FB， ∴OC⊥CG． ∴CG 是⊙O 的切线． （2）①∵OF∥CB， ∴∠AOF＝∠OBC，∠COF＝∠OCB． ∵OC＝OB， ∴∠OCB＝∠OBC． ∴∠AOF＝∠COF＝∠BOC＝60°． ∴△OBC 是等边三角形． ∵CD⊥OB，OC⊥BF， ∴点 E 是△OBC 的重心． ∴CE＝2ED＝ CD． 又∵⊙O 的半径为 ， ∴可求得：CD＝OC•sin60°＝2 × ＝3，DE＝1， ∴CE＝2； ② ． 故答案是：2π．