人教版九年级数学下册-第29章检测题 5页

第 29 章检测题 (时间：100 分钟满分：120 分) 一、选择题(每小题 3 分，共 30 分) 1．将一个圆形纸板放在太阳光下，它在地面上所形成的影子的形状不可能是( B ) A．圆 B．三角形 C．线段 D．椭圆 2．(2020·广州)如图所示的圆锥，下列说法正确的是( A ) A．该圆锥的主视图是轴对称图形 B．该圆锥的主视图是中心对称图形 C．该圆锥的主视图既是轴对称图形，又是中心对称图形 D．该圆锥的主视图既不是轴对称图形，又不是中心对称图形 第 2 题图第 4 题图 第 5 题图 第 6 题图 3．(2020·吉林)如图，由 5 个完全相同的小正方体组合成一个立体图形，它的左视图为( A ) 4．(2020·玉林)如图是由 4 个完全相同的正方体搭成的几何体，则( D ) A．三视图都相同 B．俯视图与左视图相同 C．主视图与俯视图相同 D．主视图与左视图相同 5．(2020·宜昌)诗句“横看成岭侧成峰，远近高低各不同”，意思是说要认清事物的本质， 就必须从不同角度去观察．如图是对某物体从不同角度观察的记录情况，对该物体判断最接 近本质的是( D ) A．是圆柱形物体和球形物体的组合体，里面有两个垂直的空心管 B．是圆柱形物体和球形物体的组合体，里面有两个平行的空心管 C．是圆柱形物体，里面有两个垂直的空心管 D．是圆柱形物体，里面有两个平行的空心管 6．(2020·济宁)如图是一个几何体的三视图，根据图中所示数据计算这个几何体的侧面积 是( B ) A．12πcm2B．15πcm2C．24πcm2D．30πcm2 7．(2020·菏泽)一个几何体由大小相同的小立方块搭成，它的俯视图如图所示，其中小正 方形中的数字表示在该位置小立方块的个数，则该几何体的主视图为( A ) 8．(2020·雅安)一个几何体由若干大小相同的小正方体组成，它的俯视图和左视图如图所 示，那么组成该几何体所需小正方体的个数最少为( B ) A．4B．5C．6D．7 9．(河北中考)图②是图①中长方体的三视图，若用 S 表示面积，S 主＝x2＋2x，S 左＝x2＋ x，则 S 俯＝( A ) A．x2＋3x＋2B．x2＋2C．x2＋2x＋1D．2x2＋3x 第 8 题图 第 9 题图 第 10 题图 10．如图是一个由若干个棱长为 1cm 的正方体构成的几何体的三视图，则构成这个几何 体的体积是( C ) A．3cm3B．4cm3C．5cm3D．6cm3 二、填空题(每小题 3 分，共 15 分) 11．如图是两棵小树在同一时刻的影子，可以断定这是中心投影，而不是平行投影． 第 11 题图 第 12 题图 第 13 题图 第 14 题图 12．如图，为了测量学校旗杆的高度，小东用长为 3.2m 的竹竿做测量工具．移动竹竿 使竹竿、旗杆顶端的影子恰好落在地面上同一点．此时，竹竿与这一点相距 8m，与旗杆相 距 22m，则旗杆的高度为 12m． 13．如图是由若干个大小相同的小正方体组成的几何体，那么其三种视图中面积最小的 是左视图． 14．(2020·齐齐哈尔)如图是一个几何体的三视图，依据图中给出的数据，计算出这个几 何体的侧面积是__65π__． 15．如图，在一次数学活动课上，张明用 17 个边长为 1 的小正方体搭成了一个几何体， 然后他请王亮用其他同样的小正方体在旁边再搭一个几何体，使王亮所搭几何体恰好可以和 张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状)，那么王亮至少 还需要 19 个小正方体，王亮所搭几何体的表面积为 48． 三、解答题(共 75 分) 16．(8 分)如图，将第一行的四个物体与第二行其相应的俯视图连接起来． 解：①－c，②－a，③－b，④－d 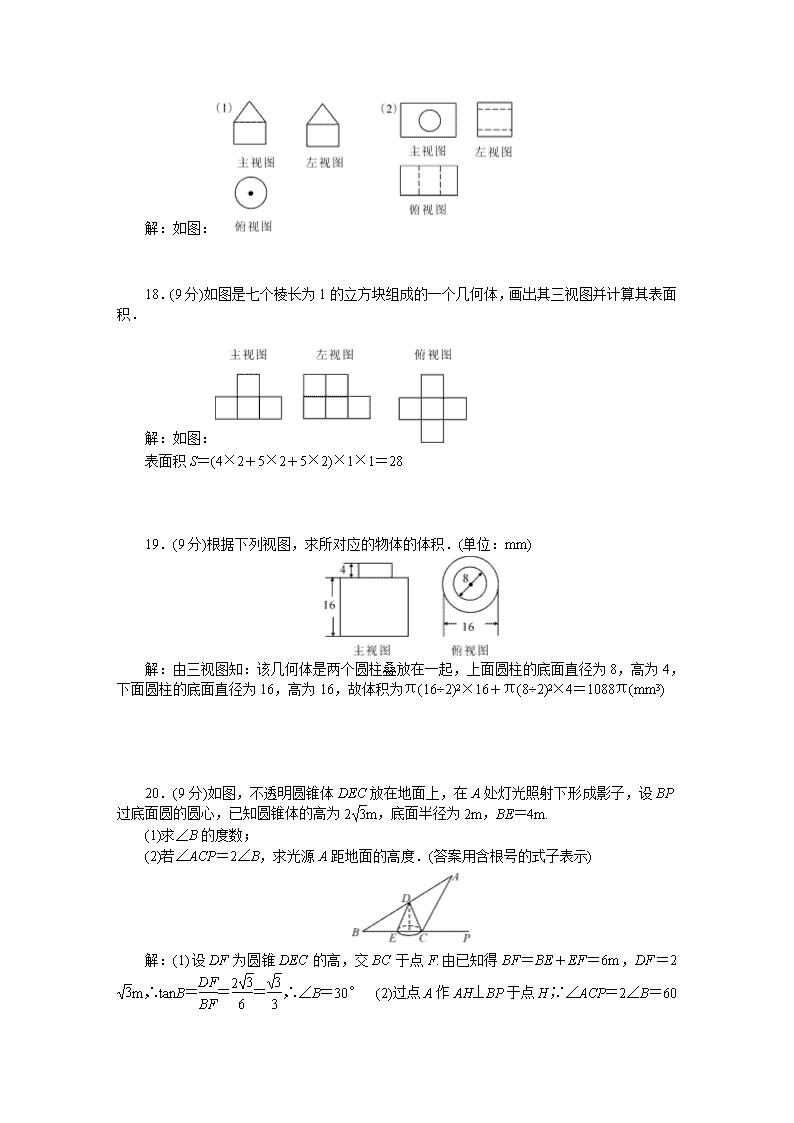17．(9 分)画出下面图形的三视图： 解：如图： 18．(9 分)如图是七个棱长为 1 的立方块组成的一个几何体，画出其三视图并计算其表面 积． 解：如图： 表面积 S＝(4×2＋5×2＋5×2)×1×1＝28 19．(9 分)根据下列视图，求所对应的物体的体积．(单位：mm) 解：由三视图知：该几何体是两个圆柱叠放在一起，上面圆柱的底面直径为 8，高为 4， 下面圆柱的底面直径为 16，高为 16，故体积为π(16÷2)2×16＋π(8÷2)2×4＝1088π(mm3) 20．(9 分)如图，不透明圆锥体 DEC 放在地面上，在 A 处灯光照射下形成影子，设 BP 过底面圆的圆心，已知圆锥体的高为 2 3m，底面半径为 2m，BE＝4m. (1)求∠B 的度数； (2)若∠ACP＝2∠B，求光源 A 距地面的高度．(答案用含根号的式子表示) 解：(1)设 DF 为圆锥 DEC 的高，交 BC 于点 F.由已知得 BF＝BE＋EF＝6m，DF＝2 3m， ∴tanB＝DF BF ＝2 3 6 ＝ 3 3 ，∴∠B＝30° (2)过点 A 作 AH⊥BP 于点 H，∵∠ACP＝2∠B＝60 °，∴∠BAC＝30°，∴AC＝BC＝8m，在 Rt△ACH 中，AH＝AC·sin∠ACP＝8× 3 2 ＝4 3(m)， ∴光源 A 距地面的高度为 4 3m 21．(10 分)如图所示，有 4 张除了正面图案不同，其余都相同的图片． (1)以上四张图片所示的立体图形中，主视图是矩形的有 B，D；(填字母序号) (2)将这四张图片背面朝上混匀，从中随机抽出一张后放回，混匀后再随机抽出一张．求 两次抽出的图片所示的立体图形中，主视图都是矩形的概率． 解：(2)列表可得 第二张 第一张 A B C D A (A，A) (A，B) (A，C) (A，D) B (B，A) (B，B) (B，C) (B，D) C (C，A) (C，B) (C，C) (C，D) D (D，A) (D，B) (D，C) (D，D) 由表可知，共有 16 种等可能结果，其中两次抽出的图片所示立体图形的主视图都是矩形 的有 4 种，分别是(B，B)，(B，D)，(D，B)，(D，D)，所以两次抽出的图片所示的立体图形 的主视图都是矩形的概率为 4 16 ，即1 4 22．(10 分)将一直径为 17cm 的圆形纸片(如图①)剪成如图②形状的纸片，再将纸片沿虚 线折叠得到正方体(如图③)形状的纸盒，则这样的纸盒体积最大为多少？ 解：如图，设小正方形的边长为 2xcm，则 AB＝4xcm，OA＝17 2 cm，在 Rt△OAB 中，有 x2＋(4x)2＝(17 2 )2，∴x＝ 17 2 ，∴小正方形的边长最大为 17cm，则纸盒体积最大为( 17)3＝ 17 17(cm3) 23．(11 分)一天晚上，李明和张龙利用灯光下的影长来测量路灯 D 的高度．如图，当李 明走到点 A 处时，张龙测得李明直立时身高 AM 与其影子长 AE 正好相等，接着李明沿 AC 方向继续向前走，走到点 B 处时，李明直立时身高 BN 的影子恰好是线段 AB，并测得 AB＝ 1.25m，已知李明直立时的身高为 1.75m，求路灯 D 的高度．(结果精确到 0.1m) 解：设 CD 长为 xm．由题意得 AM⊥EC，CD⊥EC，BN⊥EC，EA＝MA，∴AM∥CD， BN∥CD，∴EC＝CD＝x，∴△ABN∽△ACD，∴BN CD ＝AB AC ，即1.75 x ＝ 1.25 x－1.75 ，解得 x＝ 6.125≈6.1，则路灯 D 的高度约为 6.1m