2021年中考数学专题复习 专题17 全等三角形判定与性质定理（学生版） 8页

专题 17 全等三角形判定与性质定理 1.基本概念 (1)全等形：能够完全重合的两个图形叫做全等形. (2)全等三角形：能够完全重合的两个三角形叫做全等三角形. (注意对应的顶点写在对应的位置上) (3)对应顶点：全等三角形中互相重合的顶点叫做对应顶点. (4)对应边：全等三角形中互相重合的边叫做对应边. (5)对应角：全等三角形中互相重合的角叫做对应角. 2．全等三角形的表示 全等用符号“≌”表示，读作“全等于”。如△ABC≌△DEF，读作“三角形 ABC 全等于三角形 DEF”。 注：记两个全等三角形时，通常把表示对应顶点的字母写在对应的位置上。 3．全等三角形的性质：全等三角形的对应角相等、对应边相等。 4．三角形全等的判定定理 (1)边角边定理：有两边和它们的夹角对应相等的两个三角形全等(可简写成“边角边”或“SAS”) (2)角边角定理：有两角和它们的夹边对应相等的两个三角形全等(可简写成“角边角”或“ASA”) (3)边边边定理：有三边对应相等的两个三角形全等(可简写成“边边边”或“SSS”)。 (4)角角边定理：两角和其中一个角的对边对应相等的两个三角形全等(简写成 AAS). 5．直角三角形全等的判定： HL 定理：有斜边和一条直角边对应相等的两个直角三角形全等(可简写成“斜边、直角边”或“HL”) 【例题 1】(2020•甘孜州)如图，等腰△ABC 中，点 D，E 分别在腰 AB，AC 上，添加下列条件，不能判定△ ABE≌△ACD 的是( ) A．AD＝AE B．BE＝CD C．∠ADC＝∠AEB D．∠DCB＝∠EBC 【对点练习】如图，已知∠ABC=∠DCB，添加以下条件，不能判定△ABC≌△DCB 的是( ) A．∠A=∠D B．∠ACB=∠DBC C．AC=DB D．AB=DC 【例题 2】(2020•北京)如图，在△ABC 中，AB＝AC，点 D 在 BC 上(不与点 B，C 重合)．只需添加一个条 件即可证明△ABD≌△ACD，这个条件可以是 (写出一个即可)． 【对点练习】(2019 齐齐哈尔)如图，已知在△ABC 和△DEF 中，∠B＝∠E，BF＝CE，点 B、F、C、E 在同一 条直线上，若使△ABC≌△DEF，则还需添加的一个条件是 (只填一个即可)． 【例题 3】(2020•菏泽)如图，在△ABC 中，∠ACB＝90°，点 E 在 AC 的延长线上，ED⊥AB 于点 D，若 BC＝ED，求证：CE＝DB． 【对点练习】如图，点 A、D、C、F 在同一条直线上，AD=CF，AB=DE，BC=EF． (1)求证：△ABC≌DEF； (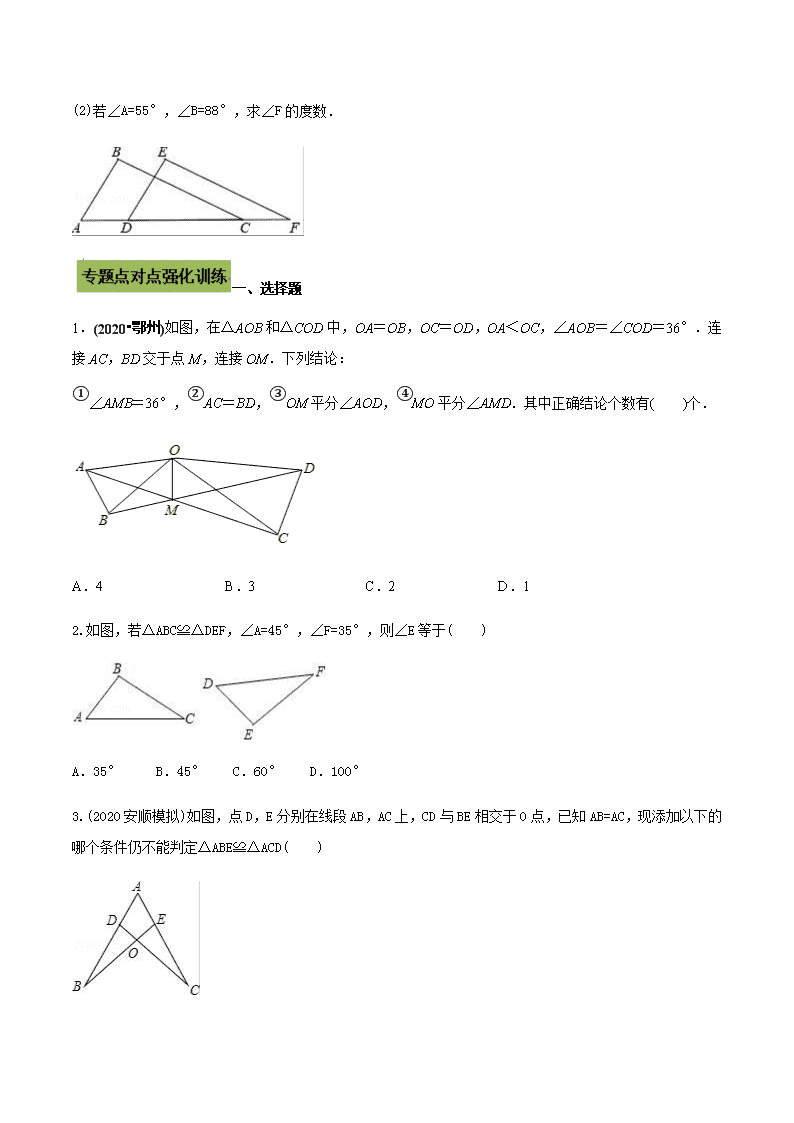2)若∠A=55°，∠B=88°，求∠F 的度数． 一、选择题 1．(2020•鄂州)如图，在△AOB 和△COD 中，OA＝OB，OC＝OD，OA＜OC，∠AOB＝∠COD＝36°．连 接 AC，BD 交于点 M，连接 OM．下列结论： ① ∠AMB＝36°， ② AC＝BD， ③ OM 平分∠AOD， ④ MO 平分∠AMD．其中正确结论个数有( )个． A．4 B．3 C．2 D．1 2.如图，若△ABC≌△DEF，∠A=45°，∠F=35°，则∠E 等于( ) A．35° B．45° C．60° D．100° 3.(2020 安顺模拟)如图，点 D，E 分别在线段 AB，AC 上，CD 与 BE 相交于 O 点，已知 AB=AC，现添加以下的 哪个条件仍不能判定△ABE≌△ACD( ) A．∠B=∠C B．AD=AE C．BD=CE D．BE=CD 4．如图，AB⊥CD，且 AB=CD．E、F 是 AD 上两点，CE⊥AD，BF⊥AD．若 CE=a，BF=b，EF=c，则 AD 的长为 ( ) A．a+c B．b+c C．a﹣b+c D．a+b﹣c 5．如图，∠ACB=90°，AC=BC．AD⊥CE，BE⊥CE，垂足分别是点 D、E，AD=3，BE=1，则 DE 的长是( ) A． B．2 C．2 D． 6．如图，△ABC≌△AEF，AB=AE，∠B=∠E，则对于结论①AC=AF，②∠FAB=∠EAB，③EF=BC，④∠EAB=∠ FAC，其中正确结论的个数是( ) A．1 个 B．2 个 C．3 个 D．4 个 二、填空题 7．(2020•齐齐哈尔)如图，已知在△ABD 和△ABC 中，∠DAB＝∠CAB，点 A、B、E 在同一条直线上，若 使△ABD≌△ABC，则还需添加的一个条件是 ．(只填一个即可) 8．(2020•辽阳)如图，在△ABC 中，M，N 分别是 AB 和 AC 的中点，连接 MN，点 E 是 CN 的中点，连接 ME 并延长，交 BC 的延长线于点 D．若 BC＝4，则 CD 的长为 9．(2020•黑龙江)如图，Rt△ABC 和 Rt △EDF 中，∠B＝∠D，在不添加任何辅助线的情况下，请你添加一个条件 ，使 Rt△ABC 和 Rt △EDF 全等． 10.(2019 四川成都)如图，在△ABC 中，AB=AC，点 D，E 都在边 BC 上，∠BAD=∠CAE，若 BD=9，则 CE 的长 为______. 11.(2019•湖南邵阳)如图，已知 AD＝AE，请你添加一个条件，使得△ADC≌△AEB，你添加的条件是 ．(不 添加任何字母和辅助线) 12．(2019•山东临沂)如图，在△ABC 中，∠ACB＝120°，BC＝4，D 为 AB 的中点，DC⊥BC，则△ABC 的面积 是 ． 三、解答题 13．(2020•南充)如图，点 C 在线段 BD 上，且 AB⊥BD，DE⊥BD，AC⊥CE，BC＝DE．求证：AB＝CD． 14．(2020•硚口区模拟)如图，点 D 在 AB 上，点 E 在 AC 上，AB＝AC，∠B＝∠C，求证：BD＝CE． 15．(2020•铜仁市)如图，∠B＝∠E，BF＝EC，AC∥DF．求证：△ABC≌△DEF． 16．(2020•无锡)如图，已知 AB∥CD，AB＝CD，BE＝CF． 求证：(1)△ABF≌△DCE； (2)AF∥DE． 17．(2020•温州)如图，在△ABC 和△DCE 中，AC＝DE，∠B＝∠DCE＝90°，点 A，C，D 依次在同一直 线上，且 AB∥DE． (1)求证：△ABC≌△DCE． (2)连结 AE，当 BC＝5，AC＝12 时，求 AE 的长． 18．(2020•常德)已知 D 是 Rt△ABC 斜边 AB 的中点，∠ACB＝90°，∠ABC＝30°，过点 D 作 Rt△DEF 使 ∠DEF＝90°，∠DFE＝30°，连接 CE 并延长 CE 到 P，使 EP＝CE，连接 BE，FP，BP，设 BC 与 DE 交 于 M，PB 与 EF 交于 N． (1)如图 1，当 D，B，F 共线时，求证： ① EB＝EP； ② ∠EFP＝30°； (2)如图 2，当 D，B，F 不共线时，连接 BF，求证：∠BFD+∠EFP＝30°． 19．(2020•黔东南州)如图 1，△ABC 和△DCE 都是等边三角形． 探究发现 (1)△BCD 与△ACE 是否全等？若全等，加以证明；若不全等，请说明理由． 拓展运用 (2)若 B、C、E 三点不在一条直线上，∠ADC＝30°，AD＝3，CD＝2，求 BD 的长． (3)若 B、C、E 三点在一条直线上(如图 2)，且△ABC 和△DCE 的边长分别为 1 和 2，求△ACD 的面积及 AD 的长．