第8章 第2节 串联、并联与混联电路-2021年初中物理竞赛及自主招生大揭秘专题突破 15页

第二节 串联、并联与混联电路 在电路中，用电器按照不同的方式连接起来，就组成了串联、并联和混联电路。不同连接方式 所对应的电压、电流等的规律也不相同。 一、串联电路 1．串联电路的定义 串联电路是指各用电器沿着单一路径顺次连接在一起，电流只沿着一条路径流动的电路。图 8.10 为常见的串联电路。 2．串联电路的规律 以图 8.10 为例，设串联电路的总电压为U ，总电流为 I ，各电 阻两端电压分别为 1U ， 2U ， 3U ，流过各电阻的电流分别为 1I ， 2I ， 3I ，串联的总电阻为 R ，则申联电路的规律可总结如下： (1)串联电路电流处处相等： 1 2 3I I I I   。 (2)串联电路两端总电压等于各电阻两端电压之和： 1 2 3U U U U   。 (3)串联电路的总电阻等于各电阻之和： 1 2 3R R R R   ；串联电路的总电阻大于其中任何一个 电阻，串联电路中任一电阻增大，总电阻也增大。 (4)串联电路各电阻两端的电压与其阻值成正比： 1 2 3 1 2 3: : : : : :U U U U R R R R 。 二、并联电路 1．并联电路的定义 各用电器连接时，首端连接在一起作为首端，尾端连接在一起作为尾端，电流分别流过各个用 电器的电路叫做并联电路。图 8.11 为常见的并联电路。 2．并联电路的规律 以图 8.11 为例，设并联电路总电压为U ，总电流为 I ，各电阻两端电 压分别为 1U ， 2U ， 3U ，流过各电阻的电流分别为 1I ， 2I ， 3I ，并联的总电 阻为 R ，则并联电路的规律可总结如下： (1)并联电路各电阻(或支路)两端电压相等： 1 2 3U U U U   。 (2)并联电路干路上的电流等于各支路电流之和： 1 2 3I I I I   。 (3) 并 联 电 路 的 总 电 阻 的 倒 数 等 于 各 支 路 电 阻 倒 数 之 和 ： 1 2 3 1 1 1 1 R R R R    ；并联电路的总电阻小于任何一个支路电阻，且总电阻与最小的支路电阻更接近。 并联电路中任一电阻增大，总电阻也增大。 (4)并联电路各电阻通过的电流与电阻阻值成反比： 1 2 3 1 2 3 1 1 1 1: : : : : :I I I I R R R R  。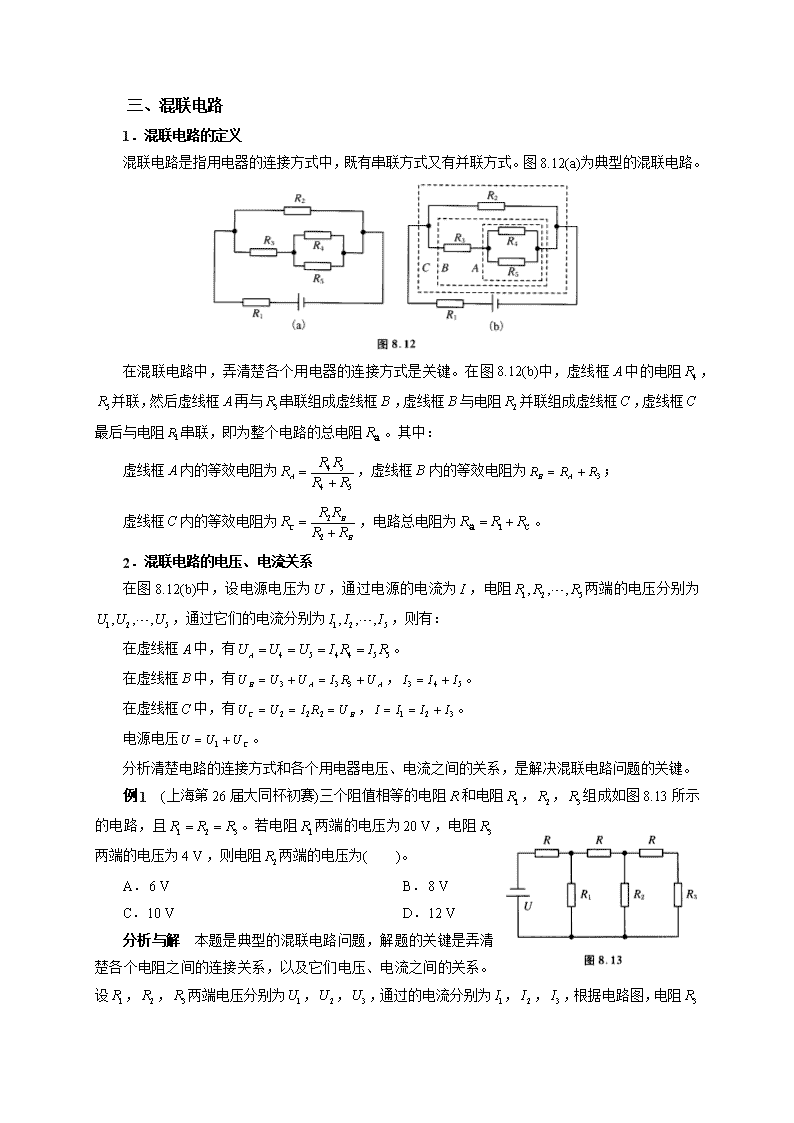 三、混联电路 1．混联电路的定义 混联电路是指用电器的连接方式中，既有串联方式又有并联方式。图 8.12(a)为典型的混联电路。 在混联电路中，弄清楚各个用电器的连接方式是关键。在图 8.12(b)中，虚线框 A 中的电阻 4R ， 5R 并联，然后虚线框 A 再与 3R 串联组成虚线框 B ，虚线框 B 与电阻 2R 并联组成虚线框 C ，虚线框 C 最后与电阻 1R 串联，即为整个电路的总电阻 R总 。其中： 虚线框 A 内的等效电阻为 4 5 4 5 A R RR R R   ，虚线框 B 内的等效电阻为 3B AR R R  ； 虚线框 C 内的等效电阻为 2 2 B C B R RR R R   ，电路总电阻为 1 CR R R 总 。 2．混联电路的电压、电流关系 在图 8.12(b)中，设电源电压为U ，通过电源的电流为 I ，电阻 1 2 5, , ,R R R 两端的电压分别为 1 2 5, , ,U U U ，通过它们的电流分别为 1 2 5, , ,I I I ，则有： 在虚线框 A 中，有 4 5 4 4 5 5AU U U I R I R    。 在虚线框 B 中，有 3 3 3B A AU U U I R U    ， 3 4 5I I I  。 在虚线框 C 中，有 2 2 2 BCU U I R U   ， 1 2 3I I I I   。 电源电压 1 CU U U  。 分析清楚电路的连接方式和各个用电器电压、电流之间的关系，是解决混联电路问题的关键。 例 1 (上海第 26 届大同杯初赛)三个阻值相等的电阻 R 和电阻 1R ， 2R ， 3R 组成如图 8.13 所示 的电路，且 1 2 3R R R  。若电阻 1R 两端的电压为 20 V ，电阻 3R 两 端的电压为 4 V ，则电阻 2R 两端的电压为( )。 A． 6 V B．8 V C．10 V D．12 V 分析与解 本题是典型的混联电路问题，解题的关键是弄清楚 各个电阻之间的连接关系，以及它们电压、电流之间的关系。设 1R ， 2R ， 3R 两端电压分别为 1U ， 2U ， 3U ，通过的电流分别为 1I ， 2I ， 3I ，根据电路图，电阻 3R 与 R 串 联后再与 2R 并联，则有 2 3 3U U I R  ① 又 3 3 3 UI R  ，代入①式，可得 2 3 3 3 3 44R RU U UR R     ② 电阻 1R 两端的电压为 1U ，等于 2U 与位于中间的电阻 R 两端电压之和，即 1 2 2 3( )U U I I R   ③ 将 2 2 2 UI R  ， 3 3 3 UI R  代入③式，并结合 1 2 3R R R  ，可得 32 1 2 2 2 3 2 3 3 3 UU R RU U R U U UR R R R           即 2 3 3 420 1 R RU R R        ④ 由②式解得 2 3 1 14 R UR   ，并代入④式，得到关于 2U 的方程： 2 2 24 96 0U U   解得 2 8 VU  或 2 12 VU   (舍去)。因此选项 B 正确。 例2 (上海第10届大同杯复赛)在图8.14所示电路中， 12 VU  (且保持不变)， 2 R   ， 1 r   ， 为了使电流表读数在同样的电阻链任意加长或减短时均保持不变，求： (1)最后一个电阻 xR 的取值。 (2)这时电流表的读数。 分析与解 (1)根据欧姆定律，电流表读数在同样的电阻链任意加长或减短时均保持不变，则电 路中的总电阻为定值，与电阻链的个数无关。考察最右端电阻链的四个电阻，显然，当这四个电阻 的总阻值恰等于 xR 时，方能符合题意。则有 1 1 1 2x xR r R R   ，代入数据，解得 ( 5 1)xR    。 (2)由题意可知总电阻 ( 5 1)xR R   总 ，电流表读数 12 A (3 5 3)A 5 1 UI R     总 。 例 3 在如图 8.15 所示电路图中， A ， B 两端电压为 12 VU  ， 1 2 4 R R   ， 3 2 R   ， 4 8 R   。 (1)若 C ， D 间接理想电压表，求电压表的读数。 (2)若 C ， D 间接理想电流表，求电流表的读数。 (3)若各个电阻阻值未知，但已知 1 2 3 4 R R R R  ，则(1)、(2)两小问的结果分别如何？ 分析与解 本题是典型的桥式电路问题，希望本题的解答可以帮助同学们理解这一模型。 (1) C ，D 间接理想电压表时，C ，D 间并没有电流。我们可以先求出电阻 1R ， 2R 两端的电压， 即 A ，C 与 A ， D 之间的电压，从而可以求出 C ， D 间的电压。如图 8.15 所示， 1R 与 3R 的电压之 和 1 3 12 VU U  ，且根据串联分压 1 1 3 3 U R U R  ，解得 1 8 VU  ， 3 4 VU  ；同理， 2 4 VU  ， 4 8 VU  。 可 见 ， A ， C 两 点 间 的 电 压 为 8 V ， A ， D 两 点 间 的 电 压 为 4 V ， 则 C ， D 间 的 电 压 8 V 4 V 4 VCDU    。 (2) C ，D 间接理想电流表时，如图 8.16(a)所示、将各个支路电流画出，并设流过电流表的电流 为 AI ，方向从 C 流向 D ，则可得 1 3 AI I I  ，只要求出 1I , 3I ，则可求出 AI 。将图 8.16(a)改画为图 8.16(b)，这不会改变通过各个电阻的电流。在图 8.16(b)中， 1R 与 2R 并联， 3R 与 4R 并联，然后两部 分再串联起来。 1R 与 2R 并联后的电阻 1 2 1 2 2 R RR R R   左 ， 3R 与 4R 并联后的电阻 3 4 3 4 1.6 R RR R R   右 ， 根据串联分压原理，可知两部分所分电压 U R U R  右 左 左 右 ，且 12 VU U 右左 ，解得 20 V3U 左 ， 16 V3U 右 ，所以 1 1 5 A3 UI R  左 ， 3 3 8 A3 UI R  右 所以 A 1 3 1 AI I I    ，可见，通过电流表的电流大小为1 A ，方向应从 D 点流向 C 点。 (3)若各电阻阻值满足 1 2 3 4 R R R R  ，在 C ， D 两点未接通时，根据串联分压规律，显然有 1 2U U ， 3 4U U ，即图 8.15 中 A ，C 两点间电压与 A ， D 两点间电压相等，则可推知 C ， D 两点间电压为 零，因此在 C ， D 间接电压表或电流表，读数都将为零。这也是一个重要结论，反过来也成立：若 C ， D 之间电流为零，则一定有 1 2 3 4 R R R R  。 练习题 1．(上海第 12 届大同杯初赛)在图 8.17 所示的电路中，电流表的读数为 I ，若要使电流表的读 数变为 4I ，则要( )。 A．在电路中串联一个电阻 2R 且 2 13R R B．在电路中串联一个电阻 2R 且 2 1 / 3R R C．在 1R 两端并联一个电阻 2R 且 2 13R R D．在 1R 两端并联一个电阻 2R 且 2 1 / 3R R 2．(上海第 13 届大同杯初赛)在如图 8.18 所示电路中，电流表 1A ， 2A ， 3A 的示数比为 5：3： 1，则电阻 1R ， 2R ， 3R 之比为( )。 A．1：3：5 B．3：5：15 C．1：1：2 D．2：2：1 3．(上海第 12 届大同杯初赛)现有四个电阻 1R ， 2R ， 3R 和 4R ，其中 1 2R R ， 3 4R R 。现将 1R 和 3R 组成串联电路， 2R 和 4R 组成并联电路，则( )。 A．串联电路的总电阻一定大于并联电路的总电阻 B．串联电路的总电阻一定小于并联电路的总电阻 C．串联电路的总电阻可能大于并联电路的总电阻 D．串联电路的总电阻可能等于并联电路的总电阻 4．(上海第 27 届大同杯初赛)在如图 8.19 所示的电路中，电阻 2 1R R ，若保持电路的总电流不 变，那么为了使通过 1R 的电流稍增大一点，可采用的措施是( )。 A．与 2R 并联一个比 2R 小得多的电阻 B．与 2R 并联一个比 2R 大得多的电阻 C．与 2R 串联一个比 2R 小得多的电阻 D．与 2R 串联一个比 2R 大得多的电阻 5．(上海第 19 届大同杯初赛)某电压表的量程为 0~3 V ，如给该电压表串联一个电阻 1R ，则电 路两端允许的最大电压为5 V ；如给该电压表串联一个电阻 2R ，则电路两端允许的最大电压为 6 V 。 现将电阻 1R 和 2R 并联后再与该电压表串联，如图 8.20 所示，则此时电路两端允许的最大电压U 为 ( )。 A．3.5 V B． 4.0 V C． 4.2 V D． 4.5 V 6．(上海第 12 届大同杯初赛)如图 8.21 所示，已知 1 2=R R ，保持电压U 不变，当电键 K 闭合后 ( )。 A．电流表、电压表的读数均不变 B．电流表读数不变，电压表读数变为原来的 2 倍 C．电压表读数不变，电流表读数变为原来的 2 倍 D．电流表、电压表的读数均变为原来的 2 倍 7．(上海第 12 届大同杯初赛)如图 8.22 所示，当 K 闭合后，电压表 1V 的示数为 4 V ，电压表 2V 的示数为 6 V ，电流表 A 的示数为1 A ，将 2R 和 3R 对换位置后， 1V ， 2V 和 A 的示数均不变，则( )。 A．通过 1R ， 2R ， 3R 的电流之和为1 A B． 1 4 R   C．电源电压为 10 VU  D． 2R 两端电压为3 V 8．(上海第 12 届大同杯初赛)在如图 8.23 所示的电路中，已知 1 2 3 4 3 R R R R     ，当电键 K 闭合时，电压表的示数为12 V ，那么电流表的示数为( )。 A．1 A B． 2 A C． 4 A D．16 A 9．(上海第 12 届大同杯初赛)在如图 8.24 所示的电路中， 1R 的电阻值为 R ， 2R ， 3R ， 4R 的电 阻值都相等，电流表的电阻忽略不计，电路两端的电压恒定不变。当电键 1K , 2K 同时合上或同时打 开时，发现电流表的示数不变，可以推知未知电阻 xR 的阻值为( )。 A．3R B． 2R C． R D． 1 2 R 10．(上海第 8 届大同杯复赛)在图 8.25 所示的电路图中，四个小灯泡完全相同。在电键 K 闭合 前，各灯都能正常发光。当电键 K 闭合后，应该出现的情况是( )。 A．各灯都比电键 K 闭合前亮 B．各灯都比电键 K 闭合前暗 C．各灯都不可能发光 D．各灯仍能正常发光 11．(上海第 26 届大同杯初赛)在如图 8.26 所示的电路中， 1V ， 2V ， 3V 是三个完全相同的电压 表。 1R ， 2R 是两个定值电阻，若电压表 1V ， 2V 的示数分别是 3 V 和1 V ，则 A ， B 之间的电压可 能为( )。 A． 7 V B． 6 V C． 5 V D． 4 V 12．(上海第 14 届大同杯初赛)如图 8.27 所示的电路较为复杂，但采用合理的估算，就可以计算 出 A 表与 mA 表的示数分别为( )。 A．0.13，30 B．0.11，10 C．0.33，30 D．0.31，10 13．(上海第 14 届大同杯初赛)图 8.28 所示电路是由 12 个不同的电阻组成的，已知 1R 12   ， 其余电阻阻值未知，测得 A ， B 间的总电阻为 6  。今将 1R 换成 6  的电阻，则 A ， B 间的总电阻 为( )。 A． 6  B． 4  C． 3  D． 2  14．(上海第 14 届大同杯初赛)在图 8.29 所示的电路中，电源电压保持不变，电键 K 闭合前，电 流表 1A ， 2A 的示数比为 5：3，电键 K 闭合后，两电流表的示数比为 3：2，则 1R ， 3R 的大小关系 是( )。 A． 1 3R R B． 1 3R R C． 1 3R R D．无法确定 15．(上海第 13 届大同杯初赛)如图 8.30 所示，滑动变阻器 R 的总电阻为 60  ，定值电阻 0 60 R   ，电源电压为18 V 。断开电键 K ，移动滑动片 P 使电压表的示数为 9 V ，然后闭合电键 K ， 则通过 0R 的电流为( )。 A． 0.12 A B． 0.15 A C． 0.24 A D． 0.45 A 16．(上海第 16 届大同杯初赛)在如图 8.31 所示的两种电路中，电源电压相同，四个电阻器的电 阻值均相等，四个电流表也完全相同，但电流表的内阻均不可忽略不计。电流表 1A ， 2A ， 3A ， 4A 八的示数分别为 1I ， 2I ， 3I ， 4I ，则下列不等式中错误的是( )。 A． 1 3I I B． 1 4I I C． 2 12I I D． 2 3 4I I I  17．(上海第 21 届大同杯初赛)如图 8.32 所示，电源电压恒为 6 V ，滑动变阻器 R 的滑片 P 位于 中点，则下列情况中，可使电阻 R 两端的电压最接近 3 V 的是( )。 A． 20 R   ， 0 200 R   B． 200 R   ， 0 400 R   C． 200 R   ， 0 200 R   D． 20 R   ， 0 400 R   18．(上海第 23 届大同杯初赛)如图 8.33 所示，图(a)，(b)中两个电路的电源完全相同，且 1 2 3 4R R R R   。则下列说法中正确的是( )。 A．电流表 1A 没有示数，电流表 2A 有示数 B．电流表 1A ， 2A 都有示数，且示数相同 C．电流表 1A ， 2A 都有示数，且电流表 1A 的示数 较大 D．电流表 1A ， 2A 都有示数，且电流表 2A 的示数 较大 19．(上海第 28 届大同杯初赛)在如图 8.34 所示的电路中，W 为一个稳压管，其作用是确保 C ， D 之间的电压 CDU 不变，只要流过稳压管W 的电流在5 mA 和 25 mA 之间， CDU 将稳定为15 V 。 2R 为一可变电阻，它的最小值为1000  ，最大值为无穷大(即断路)。设电源电压U 为 25 V ，则当 2R 变 化时，为了确保 CDU 为15 V ， 1R 的阻值范围应为( )。 A． 250 ~ 2000  B． 400 ~ 500  C． 250 ~ 400  D． 500 ~ 2000  20．(上海第 29 届大同杯初赛)在如图 8.35 所示的电路中，电阻 1R 标有“ 6  ，1 A ”， 2R 标有 “3  ，1.2 A ”，电流表 1A ， 2A 的量程均为 0 ~ 3 A ，电压表的量程为 0 ~ 15 V ，在 a ，b 间接入电 压可调的电源。闭合电键 S 后，为保证 1R ， 2R 均不损坏，则允许的最大电源电压和此时通过电流表 1A 的电流分别为( )。 A．9 V ，1 A B． 3.6 V ，1.8 A C． 9.6 V ，1 A D．3.6 V ， 2.2 A 21．(上海第 31 届大同杯初赛)在如图 8.36 所示的电路中，电阻 1R 和 2R 并联，则三个电表中( )。 A．表 1、表 2 是电流表，表 3 是电压表 B．表 1、表 2 是电压表，表 3 是电流表 C．表 1、表 2、表 3 都是电流表 D．表 1、表 2、表 3 都是电压表 22．(上海第 22 届大同杯复赛)如图 8.37(a)所示，在一个电阻均匀的金属圆环上有 A ， B ， C ， D 四点。其中 O 为圆心， AB ， CD 为圆环的两条互相垂直的直径。现把 A ， B 两点接入电源电压 保持不变的如图 9.39(b)所示的电路 MN 两端时，发现电流表示数为 0I ，当换接 A ，D 两点时，电流 表的示数应为( )。 A． 0 / 4I B． 03 / 4I C． 0I D． 04 / 3I 23．(上海第 32 届大同杯初赛)在如图 8.38 所示的电路中，电源电压U 保持不变。 1R 为定值电 阻， 2R 为滑动变阻器，且 bc cdabR R R  ，闭合电键S ，移动滑片 P 至 b 点时，电压表示数为1 V ； 移动滑片 P 至 d 点时，电压表示数为 2 V ；移动滑片 P 至 c 点时，电压表示数为( )。 A．1.2 V B．1.5 V C．1.6 V D．1.8 V 24．(上海第 12 届大同杯初赛)在图 8.39 所示的电路中，电源电压为10 V ，定值电阻为 30  ， 滑动变阻器标有“ 60  ，5 A ”字样，则该电路正常使用时总电阻的变化范围是( )。 A． 0 ~ 20  B．1.9 ~ 20  C． 20 ~ 60  D． 20 ~ 30  25．(上海第 17 届大同杯初赛)在图 8.40 所示电路中，已知 0 17.6 R   ，将 K 接通 a 时，电阻 1R 的电压为1 V ，流过电阻 2R 的电流为 0.2 A ，将 K 接通b 时，电阻 1R 的电压为1.2 V ，流过电阻 2R 的 电流为 0.15 A ，则电阻 xR 的阻值为________  ，电阻 1R 的阻值为________  。 26．(上海第 7 届大同杯复赛)如图 8.41 所示，若每个电阻的阻值均为1  ，则 ab 两端的总电阻 abR 是________  。 27．(上海第 7 届大同杯复赛)如图 8.42 所示，已知 1 3 2 42 2R R R R   ， 2A 的示数为 0.5 A ， 3A 的示数为 0.3 A ，则 1A 的示数为________ A 。 28．(上海第 10 届大同杯复赛)在图 8.43 所示的电路中，电阻 1 10 R   ， 2 4 R   ， 3 6 R   ， 4 3 R   ，电压 12 VU  且保持不变。如在 a ， b 间接一电阻，使流过 3R 的电流为零，则 R 的阻值 为_________；如在 a ， b 间接一电压表，其读数为________ V ；如在 a ， b 间接一电流表，其读数 为________ A 。(电压表、电流表的内阻对电路的影响可以忽略) 29．(上海第 2 届大同杯复赛)在图 8.44 中，电源电压 12 VU  ， 1 10 R   ， 2 30 R   ， 3 10 R   ， 闭合电键 K 后，电流表的读数 1 0.3 AI  。求：电压表读数和变阻器 R 中通有电流的那部分的电阻值。 30．(上海第 4 届大同杯复赛)在图 8.45 所示的电路中， 1 6 R   ，电源电压为 9 V ，电压表的示 数为 6 V ，电流表的示数为1 A 。如果再取一个定值电阻 R 接入电路，要使电流表的示数变为1.5 A ， 试问： (1) 2R 的阻值为多大？ (2) R 的阻值应为多大，以什么方式接入电路？ (3) R 接人电路后，电压表的读数为多少？ 参考答案 1．D。电流表读数由 I 变为 4I ，总电阻应从 1R 变为 1 1 4 R ，应将 2R 与 1R 并联，且应有 2 1 1 1 1 4 R R R   ， 解得 1 2 3 RR  。 2．C。提示：题中三个电阻并联， 1A 测总电流， 2A 测通过 2R 与 3R 的电流之和， 3A 测通过 3R 的 电流。 3．A。提示：串联的总电阻大于 1R ，并联的总电阻小于 2R ，考虑到 1 2R R ，选项 A 正确。 4．C。设总电流为 I ，通过 1R ， 2R 的电流分别为 1I ， 2I ，则根据并联电路的规律，有 1I 2I I  ， 1 1 2 2I R I R ，解得 2 1 11 2 2 1 R I II RR R R    。可见，在总电流 I 不变时， 1I 的大小依赖于 1 2 R R 的大小，当 2R 略微增大(即与 2R 串联一个比 2R 小得多的电阻，使得原 2R 支路电阻略微变大)， 1 2 R R 略微变小，从而 1I 略微增大。 5．C。电路两端达到允许的最大电压时，电压表应达到最大量程，即通过电压表的电流为满偏 电流 mI ，电路两端的电压超出电压表量程的部分由定值电阻分担，则 m 1 2 VI R  ， m 2 3 VI R  ，设 1R 和 2R 并联后分担的最大电压为U并 ，则 1 2 m 1 2 R RI UR R   并 ，可解得并U 并 1.2 V ，因此此时整个电路 两端允许的最大电压为 4.2 VU  。 6．D。电键 K 闭合时，电流表的读数为 2 U R ，电压表的读数为U ；电键 K 断开时，电流表的读 数为 1 2 22 U U R R R  ，电压表的读数为 2 U 。 7．D。电路中三个电阻为串联，电流均为1 A ，选项 A 错误；电压表 1V 的示数等于 1R 与 2R 电 压之和，即 1 2 4 VU U  ，电压表 2V 的示数等于 2R 与 3R 电压之和，即 2 3 6 VU U  ，又 2R 和 3R 对 换位置后， 1V 的示数不变，可知 2 3R R ，即 2 3 3 VU U  ， 1 1 VU  ，电源电压为 7 VU  ，电阻 1 1 1 UR I    ，选项 D 正确。 8．B。由电路图知电压表测电源电压，则电源电压为12 V ，电阻 2R ， 3R ， 4R 并联，并联部分 总电阻为1  ，然后再与 1R 串联，由分压关系，电阻 1R 两端电压为 9 V ，并联部分电压为 3 V ，则 并联部分每个支路的电流为1 A 。电流表测通过 2R 与 3R 的电流之和，因此其示数为 2 A 。 9．A。设 1K ， 2K 闭合前后电流表示数始终为 I ，设 2 3 4R R R r   。电键 1K ， 2K 闭合前，电 阻 1R ， 2R ， 3R 串联， 2R 与 3R 的电压之和 2 3( ) 2U I R R Ir    ；电键 1K ， 2K 闭合后， xR 与 1R 并联， 3R 与 4R 并联，这两个并联部分再与 2R 串联。此时 2R 与 3R ， 4R 的总电阻为 3 2 r ，由于流过 1R 的电流 仍为 I ， 1R 与 xR 并联后的电压不变，因此其余部分电压仍为U 。电路中的总电流等于流过 1R 与 xR 的电流之和，即 x IRI IR    ，则 3 3 2 2x IRU I r I rR          ，将两个含有U  的式子联立解得 3xR R 。 10．D。提示：四个灯泡完全相同，开关S 闭合后，并没有电流通过S 。 11．AC。依题意，三个电压表内阻相同，电压表内阻不能视为无穷大，要考虑流过电压表的电 流。A ，B 之间的电压等于电压表 1V 和 3V 的示数之和。两个电阻与电压表之间为桥式连接，求解 3V 的示数时，判断通过 2V 的电流方向是关键。不妨设 A 点接电源正极，B 点接电源负极，设通过 1V 的 电流为3I ，方向向右，则通过 2V 的电流为 I ，方向可能向左也可能向右。若通过 2V 的电流 I 向左， 则通过 3V 的电流为3 2I I I  ， 3V 的示数为 2 V ， A ， B 之间的电压为5 V ；若通过 2V 的电流 I 向 右，则通过 3V 的电流为 3 4I I I  ， 3V 的示数为 4 V ， A ， B 之间的电压为 7 V 。 12．A。最上面的两个电阻串联后总阻值为 2000  ，然后再与10  的电阻并联，则并联后的总 阻值近似为10  ，再与左边一个1000  的电阻串联后总阻值近似为1000  ，这样，电路就近似等 效为一个 1000  和一个 300  的电阻并联，最后的总电阻约为 230  ，因此 A 表的读数为 30 V 0.13 A230  ，电流表 mA 的读数为 30 V 30 mA1000  。选项 A 正确。 13．B。将 xR 以外的部分视为一个电阻 R ，则 1 1 1 6 12 R   ，解得 12 R   ，则当将 1R 换成 6  的 电阻时， 1 1 1 6R R  总 ，解得 =4 R 总 。 14．A。设电键 K 闭合前后，两电流表读数分别为 1I ， 2I 和 1I  ， 2I  ，则 K 闭合前， 1 2 2 1 2 2 3 R I R I I   ； 设 K 闭合后， 2R 与 3R 并联后的等效电阻为 R并 ，则 1 2 1 2 2R I R I I   并 ，又 2 3 2 3 = R R RR R并 ，由以上关系 解得 3 12R R 。选项 A 正确。 15．A。断开电键时电压表的读数为9 V ，说明滑片在变阻器中央，滑片以下部分的阻值为30  。 闭合电键后，变阻器滑片以下的部分与 0R 并联，并联部分阻值 60 30 60 30R  并 20   ，则并联部分 所分的电压 18 V 20 7.2 V30 20 U      并 ，通过 0R 的电流为 7.2 V 0.12 A60 I  。 16．C。设电源电压为U ，电流表内阻均为 r ，再设 1A 与一个 R 串联后的电压之和为U ，显然 由 欧 姆 定 律 ， 得 1 UI R r   ， 3 4 UI I R r    ， 显 然 选 项 AB 正 确 ； 又 2 RI U U R r    1 2 2U U U IR r R r R r         ，选项 C 错误；由于 2I 与 3 4I I 分别是左右两个电路的总 电流，在电源电压相等时，比较总电流的大小关系，可以从比较两个电路的总电阻入手。左边电路 的 总 电 阻 ( ) ( ) R R rR rR R r   左 ， 右 边 电 路 的 总 电 阻 2 R rR 右 ， ( ) ( ) R R r rR R rR R    右左 2 02 2 R r Rr R r    ，可见 R R 右左 ，因此 2 3 4I I I  ，选项 D 正确。 17．D。 0R 与滑动变阻器的下半部分并联，并联部分的总电阻越接近 1 2 R ，并联部分所分的电 压就越接近电源电压的一半。 0 0 0 1 1 12 1 2 12 2 R R R RR R R R       并 ，可见，R 越小， 0R 越大，R并 越接近 1 2 R ， 选项 D 正确。 18．D。四个电阻的阻值不满足 31 2 4 RR R R  ，则 1A ， 2A 的读数均不为零。设在图 8.33(a)中，通过 1R ， 2R ， 3R ， 4R 的电流分别为 1I ， 2I ， 3I ， 4I ，显然，图 8.33(b)中各个电阻通过的电流也对应地 分别为 1I ， 2I ， 3I ， 4I ，各电阻电流方向均向右。则电流表 2A 的读数为 A2 1 2I I I  。通过 1A 的电 流 1AI 可能向上，也可能向下，若 A1I 向上，则 A1 2 4I I I  ；若 A1I 向下，则 A1 1 3I I I  ，故 2A 的读数 一定大于 1A 。 19．B。稳压管的电压为15 V 不变，则 1R 两端电压为10 V 不变。当 2R 的阻值为1000  时，通 过 2R 的电流为15 mA ，通过 1R 的电流范围是 20 mA 到 40 mA ，可求得 1R 的阻值范围为 250 ~ 500  。 当 2R 的阻值为无穷大时，通过 2R 的电流为零，通过 1R 的电流范围是 5 mA 到 25 mA ，可求得 1R 的阻 值范围为 400 ~ 2000  。而这两部分的公共部分是 400 ~ 500  ，选项 B 正确。 20．B。让 2R 通过的电流为1.2 A ，则电压表读数为 3.6 V ，通过 1R 的电流为 0.6 A ，电流表 1A 的示数为1.8 A 。 21．A。略。 22．D。提示：设 1 4 圆周导线的电阻为 R ，则 A ， B 两点接入电路时， A ， B 间的等效电阻 2 2 2 2AB R RR RR R   ，电流表的读数 0 AB U UI R R   。 A ， D 两点接入电路时， A ， D 间的等效电阻 3 3 3 4AD R RR RR R   ，电流表的读数 0 0 4 4 3 3AD U UI IR R     。 23．C。不妨设 0ab bc cdR R R R   ，则滑片在 b 点时，电路中的电流为 1 0 b UI R R   电压表的读 数为 0 0 1 0 1 Vab b URU I R R R    ；同理，滑片滑至 d 点时，电压表示数 03dadU I R  0 1 0 3 2 V3 U R R R   ， 可 解 得 1 03R R ， 4 VU  ， 则 滑 片 滑 至 c 点 时 ， 电 压 表 读 数 为 02cacU I R   0 0 1 0 0 0 2 4 V 2 2 3 2 U R R R R R R    1.6 V 。 24．B。变阻器连人电路的阻值为 60  时，总电阻最大值 max 60 30 20 60 30R     ，当变阻器通 过的电流为5 A 时，变阻器连人的电阻为 2  ，总电阻最小值 min 2 30 1.9 2 30R     。 25.7，3080。K 接b 时，电阻 1R 两端的电压等于电源电压U ，即 1.2 VU  。K 接 a 时， 1R 两端 的电压为1 V ，则 2R 两端的电压为 0.2 V ， 2 0.2 V 1 0.2 AR    ，且 0R ， 1R ， xR 的电流之和等于 0.2 A ， 有 1 1 1 1 0.2 A17.6 xR R    。在 K 接 b 时， 2R 两端的电压为 0.15 V ， 1R 两端的电压为1.05 V ，则 1 1.05 V 7 0.15 AR    ，由此可解得 3080 xR   。 26.3。提示：自右向左逐个求解等效阻值即可。 27.0.6。由电路图可知四个电阻并联， 3A 的示数等于通过 3R ， 4R 的电流之和， 2A 的示数等于 通过 2R ， 3R ， 4R 的电流之和，因此通过 2R 的电流为 2 0.2 AI  。并联的各支路电阻之比等于电阻的 反比，则 1 3 2 1 0.1 A2I I I   ， 4 2 0.2 AI I  ，则 1A 的示数为 1 2 3I I I  4 0.6 AI  。 28．1.2  ；9；10 3 。若要使得流过 3R 的电流为零，则其余四个电阻必须满足 4 2 1 RR R R  ，可解得 1.2 R   。当 a ，b 间接电压表时，电路的连接方式为 2R 与 3R 串联后再与 1R 并联，最后并联部分再 与 4R 串联。电压实际测量的是电阻 3R 与 4R 的电压之和，等效电路图如图 8.46(a)所示。易得 1R ， 2R ， 3R 的总阻值为 5  ，则由分压关系可知 4R 两端的电压为 4.5 V ， 3R 两端电压为 4.5 V ，因此电压表 读数为9 V 。当 a ，b 间接电流表时，电路的连接方式变为 3R ， 4R 并联，然后再与 1R 串联，最后这 整个部分再与 2R 并联，电流表测量的是通过电阻 2R 与 3R 的电流之和，等效电路图如图 8.46(b)所示。 容易求得通过 2R 的电流为 3 A ，通过 3R 的电流为 1 A3 ，则电流表的示数为 10 A3 3。 29．电阻 2R 两端的电压 2 1 1 1 0.3 10 V 3 VU U I R     ，通过 2R 的电流 2 2 2 3 V 30 UI R    0.1 A ， 通 过 变 阻 器 和 电 阻 3R 的 电 流 3 1 2 0.3 A 0.1 A 0.4 AI I I     ， 电 压 表 的 读 数 vU  2 3 3 3 V 0.4 A 10 7 VU I R      ，变阻器两端的电压 v 12 V 7 V 5 VRU U U     ，变阻 器连人电路的阻值 3 5 V 12.5 0.4 A RUR I     。 30．(1) 2 1 2 2 9 6 3 1 U U UR I I        。 (2) R 接入电路前，电路的总电阻 9 9 1R U I     总 ， R 接入电路后，电路的总电阻 9 6 1.5 UR I      总 ，可见，接入 R 后总电阻减小了 3  ， R 只能并联在电路中。 ①若 R 并联在 a ，b 之间，则并联后 a ，b 之间的阻值应为 3 3 abR R    总 ，故有 1 1 1 1 abR R R   ， 解得 6 R   。 ②若 R 并联在 a ，b 之间，则并联后 a ，b 之间的阻值应为 6 acR R  总 ，故有 1 acR  1 2 1 1 R R R  ， 解得 18 R   。 ③若 R 并联在 b ， c 之间，则并联后 b ， c 之间的阻值应为 1 0bcR R R  总 ，显然只有将无阻 值的导线接在 b ， c 之间才能满足 0bcR  ，这不符合题意。 (3)将 R 并联在不同的位置，电压表的读数不同。 ① 当 R 并 联 在 a ， b 之 间 时 ， 2 3 abR R   ， 根 据 串 联 分 压 规 律 ， 电 压 表 示 数 1 abU U 1 4.5 V2U  。 ②当 R 并联在 a ， b 之间时，并未影响 1R ， 2R 所在的这条支路，因此 1 6 VU  。