- 67.00 KB
- 2021-11-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
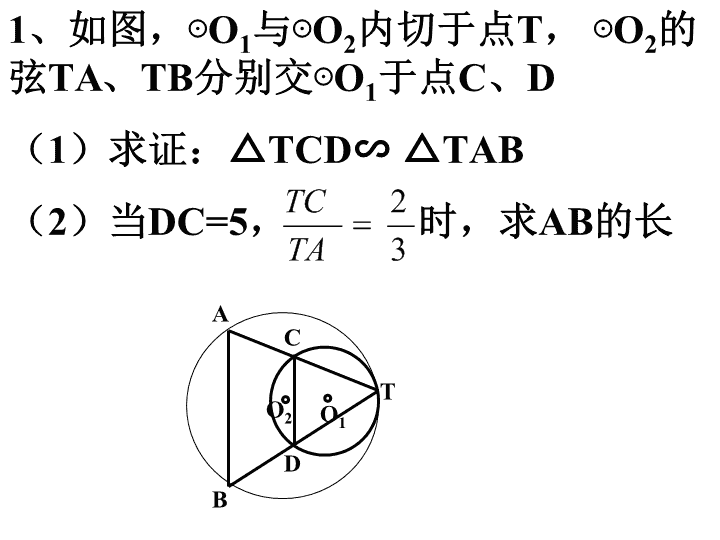
1、如图,⊙
O
1
与⊙
O
2
内切于点
T,
⊙
O
2
的弦
TA、TB
分别交⊙
O
1
于点
C、D
(1)
求证:△
TCD∽
△
TAB
(2)
当
DC=5,
时,求
AB
的长
O
1
O
2
T
A
B
C
D
2、如图,已知⊙
O
1
与⊙
O
2
内切于点
T,
⊙
O
2
的弦
AB
切⊙
O
1
于
C,
连结
CT,
求证:
TC
平分∠
ATB
C
O
1
O
2
T
A
B
变化:
“⊙
O
2
的弦
AB
与⊙
O
1
相交”会有什么结论?
3、如图,
⊙
O
1
与⊙
O
2
内切于点
A,O
2
在⊙
O
1
上,
B
是
O
2
A
上一点,
BD⊥OA
交⊙
O
2
于
D,
交⊙
O
1
于
C,
连结
AD
交⊙
O
1
于
E,
则(1)
E
是
AD
上一个怎样的点?试证明,(2)
AD
与
AC
是怎样的倍数关系?写出关系式,并证明。
O
2
O
1
A
D
E
B
C
4、如图,已知⊙
O
1
与⊙
O
2
外切于
M
点,
AC
是两圆的外公切线,
A、C
为切点,连
AM
并延长交⊙
O
2
于
D
(1)
求证:
CM
2
=AM·MD
D
A
C
M
O
1
O
2
4、如图,已知⊙
O
1
与⊙
O
2
外切于
M
点,
AC
是两圆的外公切线,
A、C
为切点,连
AM
并延长交⊙
O
2
于
D
(2)
如图,若移动点
A,AC
保持与相切⊙
O
2
于
C,AC
交⊙
O
1
于
B,
则
CM
2
=______(
请在横线上填写图中的两条线段的乘积)并证明之。
D
A
C
M
O
1
O
2
B
4、如图,已知⊙
O
1
与⊙
O
2
外切于
M
点,
AC
是两圆的外公切线,
A、C
为切点,连
AM
并延长交⊙
O
2
于
D。
(3)如图,将圆的外公切线变为两圆的割线,交点分别为
A、B、C、E,
则
MC·ME=______(
请在横线上填写图中的某两条线段的乘积)并证明之。
D
A
C
M
O
1
O
2
B
E
变式:
如图, ⊙
O
1
与⊙
O
2
外切于
P,AB
过点
P,
分别交⊙
O
1
和⊙
O
2
于
A、B,BH
切⊙
O
2
于
B,
交⊙
O
1
于
C、H。
(1)
求证:△
BCP∽
△
HAP
(2)若
AP:PB=3:2,
且
C
为
HB
的中点,求
AH:BC
A
C
P
O
1
O
2
B
H
相关文档
- 鄂尔多斯专版2020中考数学复习方案2021-11-1110页
- 2020年北京市燕山区中考数学一模试2021-11-1137页
- 2012年江苏省连云港中考数学试题(含2021-11-1123页
- 2018年广西玉林市中考数学试卷2021-11-1126页
- 2018中考数学试题分类:考点6 分式2021-11-114页
- 2020年山东省泰安市中考数学试卷2021-11-1133页
- 2020年四川省成都市中考数学试卷2021-11-1127页
- 2021年中考数学复习《中考压轴题中2021-11-118页
- 必备中考数学专题复习课件第一部分2021-11-1142页
- 2020年河南省开封市中考数学二模试2021-11-1126页