2019江苏省南京市中考数学试题（word版，含答案） 11页

南京市 2019 年初中学业水平考试 数 学 一、选择题（本大题共 6 小题，每小题 2 分，共 12 分．在每小题所给出的四个选项中，只 有一项是正确的，请把正确选项前的字母代号填涂在答题卡相应位置．．．．．．．上） 1．2018 年中国与“一带一路”沿线国家货物贸易进出口总额达到 13 000 亿美元．用科学记 数法表示 13 000 是 A． 50.13 10 B． 41.3 10 C． 313 10 D． 2130 10 2．计算 2 3( )a b 的结果是 A． 2 3a b B． 5 3a b C． 6a b D． 6 3a b 3．面积为 4 的正方形的边长是 A．4 的平方根 B．4 的算术平方根 C．4 开平方的结果 D．4 的立方根 4．实数 a、b、c 满足 a＞b 且 ac＜bc，它们在数轴上的对应点的位置可以是 5．下列整数中，与10 13 最接近的是 A．4 B．5 C．6 D．7 6．如图，△A′B′C′是由△ABC 经过平移得到的，△A′B′C′还可以看作是△ABC 经过怎样的 图形变化得 到？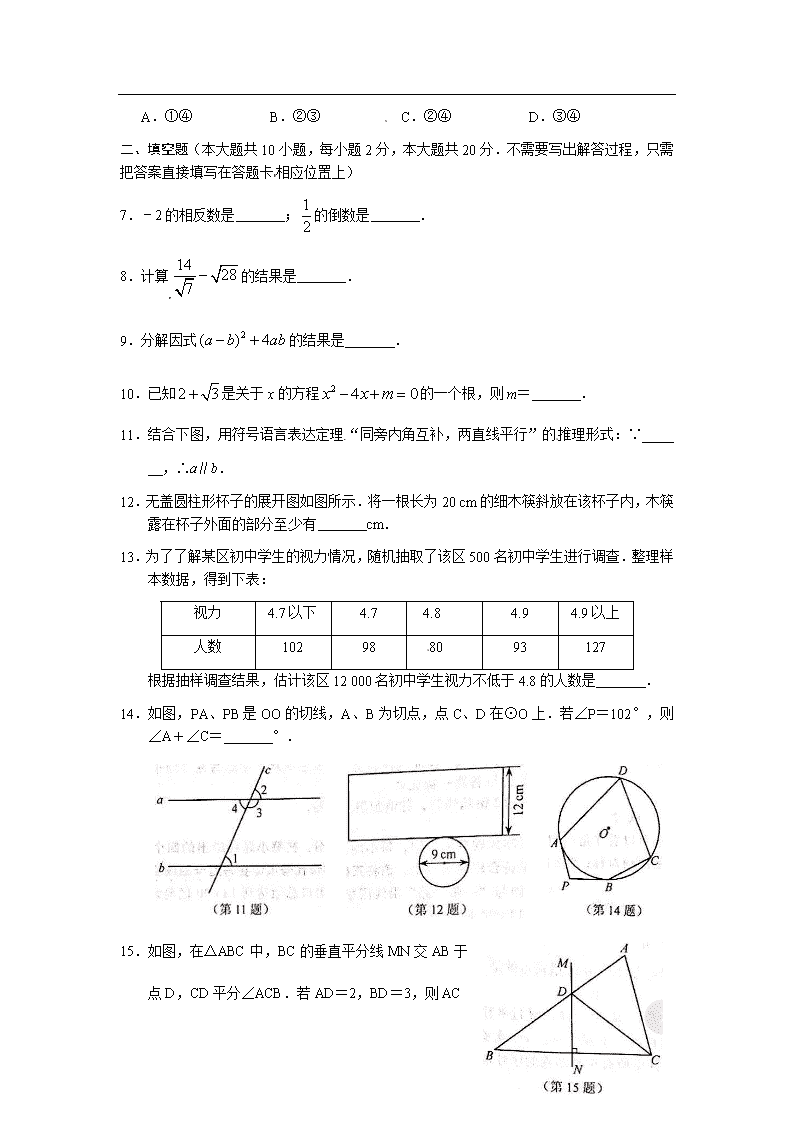下列结论： ①1 次旋转； ②1 次旋转和 1次轴对称； ③2 次旋转； ④2 次轴对称． 其中所有正确结论的序号是 A．①④ B．②③ C．②④ D．③④ 二、填空题（本大题共 10 小题，每小题 2 分，本大题共 20 分．不需要写出解答过程，只需 把答案直接填写在答题卡．．．相应位置．．．．上） 7．﹣2 的相反数是 ； 1 2 的倒数是 ． 8．计算 14 28 7  的结果是 ． 9．分解因式 2( ) 4a b ab  的结果是 ． 10．已知 2 3 是关于 x 的方程 2 4 0x x m   的一个根，则 m＝ ． 11．结合下图，用符号语言表达定理“同旁内角互补，两直线平行”的推理形式：∵ ，∴a∥b． 12．无盖圆柱形杯子的展开图如图所示．将一根长为 20 cm 的细木筷斜放在该杯子内，木筷 露在杯子外面的部分至少有 cm． 13．为了了解某区初中学生的视力情况，随机抽取了该区 500 名初中学生进行调查．整理样 本数据，得到下表： 视力 4.7 以下 4.7 4.8[来源:学科网 ZXXK] 4.9 4.9 以上 人数 102 98 80[来源:Zxxk.Com] 93 127 根据抽样调查结果，估计该区 12 000 名初中学生视力不低于 4.8 的人数是 ． 14．如图，PA、PB 是 OO 的切线，A、B 为切点，点 C、D 在⊙O 上．若∠P＝102°，则 ∠A＋∠C＝ °． 15．如图，在△ABC 中，BC 的垂直平分线 MN 交 AB 于 点 D，CD 平分∠ACB．若 AD＝2，BD＝3，则 AC 的长为 ． 16．在△ABC 中，AB＝4，∠C＝60°，∠A＞∠B，则 BC 的长的取值范围是 ． 三、解答题（本大题共 11 小题，共 88 分．请在答题卡．．．指定区域．．．．内作答，解答时应写出文字 说明、证明过程或演算步骤） 17．（7 分）计算 2 2( )( )x y x xy y   ． 18．（7 分）解方程 2 311 1 x x x    ． 19．（7 分）如图，D 是△ABC 的边 AB 的中点，DE∥BC，CE∥AB，AC 与 DE 相交于点 F．求 证△ADF≌△CEF． 20．（8 分）下图是某市连续 5 天的天气情况． （1）利用方差判断该市这 5 天的日最高气温波动大还是日最低气温波动大； （2）根据上图提供的信息，请再写出两个不同类型的结论． 21．（8 分）某校计划在暑假第二周的星期一至星期四开展社会实践活动，要求每位学生选 择两天参加活动． （1）甲同学随机选择两天，其中有一天是星期二的概率是多少？ （2）乙同学随机选择连续的两天，其中有一天是星期二的概率是 ． 22．（7 分）如图，⊙O 的弦 AB、CD 的延长线相交于点 P，且 AB＝CD．求证 PA＝PC． 23．（8 分）已知一次函数 1 2y kx  （k 为常数，k≠0）和 2 3y x  ． （1）当 k＝﹣2 时，若 1y ＞ 2y ，求 x 的取值范围； （2）当x＜1 时， 1y ＞ 2y ．结合图像，直接写出 k 的取值范围． 24．（8 分）如图，山顶有一塔 AB，塔高 33 m．计划在塔的正下方沿直线 CD 开通穿山隧 道 EF．从与 E 点相距 80 m 的 C 处测得 A、B 的仰角分别为 27°、22 °，从与 F 点相距 50 m 的 D 处测得 A 的仰角为 45°．求隧道 EF 的长度． （参考数据：tan22°≈0.40，tan27°≈0.51） 25．（8 分）某地计划对矩形广场进行扩建改造．如图，原广场长 50m，宽 40m，要求扩充 后的矩形广场长与宽的比为 3：2．扩充区域的扩建费用每平方米 30 元，扩建后在原广 场和扩充区域都铺设地砖，铺设地砖费用每平方米 100 元．如果计划总费用 642 000 元， 扩充后广场的长和宽应分别是多少米？ 26．（9 分）如图①，在 Rt△ABC 中，∠C＝90°，AC＝3，BC＝4．求作菱形 DEFG，使点 D 在边 AC 上，点 E、F 在边 AB 上，点 G 在边 BC 上． （1）证明小明所作的四边形 DEFG 是菱形； （2）小明进一步探索，发现可作出的菱形的个数随着点 D 的位置变化而变化……请你 继续探索，直接写出菱形的个数及对应的 CD 的长的取值范围． [来源:学科网 ZXXK] 27．（11 分） 【概念认知】[来源:学科网 ZXXK] 城市的许多街道是相互垂直或平行的，因此，往往不能沿直线行走到达目的地，只能按 直角拐弯的方式行走．可以按照街道的垂直和平行方向建立平面直角坐标系 xOy，对两 点 A( 1x ， 1y )和 B( 2x ， 2y )，用以下方式定义两点间距离：d(A，B)＝ 1 2x x ＋ 1 2y y ． 【数学理解】 （1）①已知点 A(﹣2，1)，则 d(O，A)＝ ； ②函数 2 4y x   (0≤x≤2)的图像如图① 所示，B 是图像上一点，d(O，B)＝3， 则点 B 的坐标是 ． （2）函数 4y x  (x＞0)的图像如图②所示，求证：该函数的图像上不存在点 C，使 d(O， C)＝3． （3）函数 2 5 7y x x   (x≥0)的图像如图③所示，D 是图像上一点，求 d(O，D)的最 小值及对应的点 D 的坐标． 【问题解决】 （4）某市要修建一条通往景观湖的道路，如图④，道路以 M 为起点，先沿 MN 方向到 某处，再在该处拐一次直角弯沿直线到湖边，如何修建能使道路最短？（要求： 建立适当的平面直角坐标系，画出示意图并简要说明理由） [来源:学+科+网 Z+X+X+K]