山东省日照市2017年中考数学试题 12页

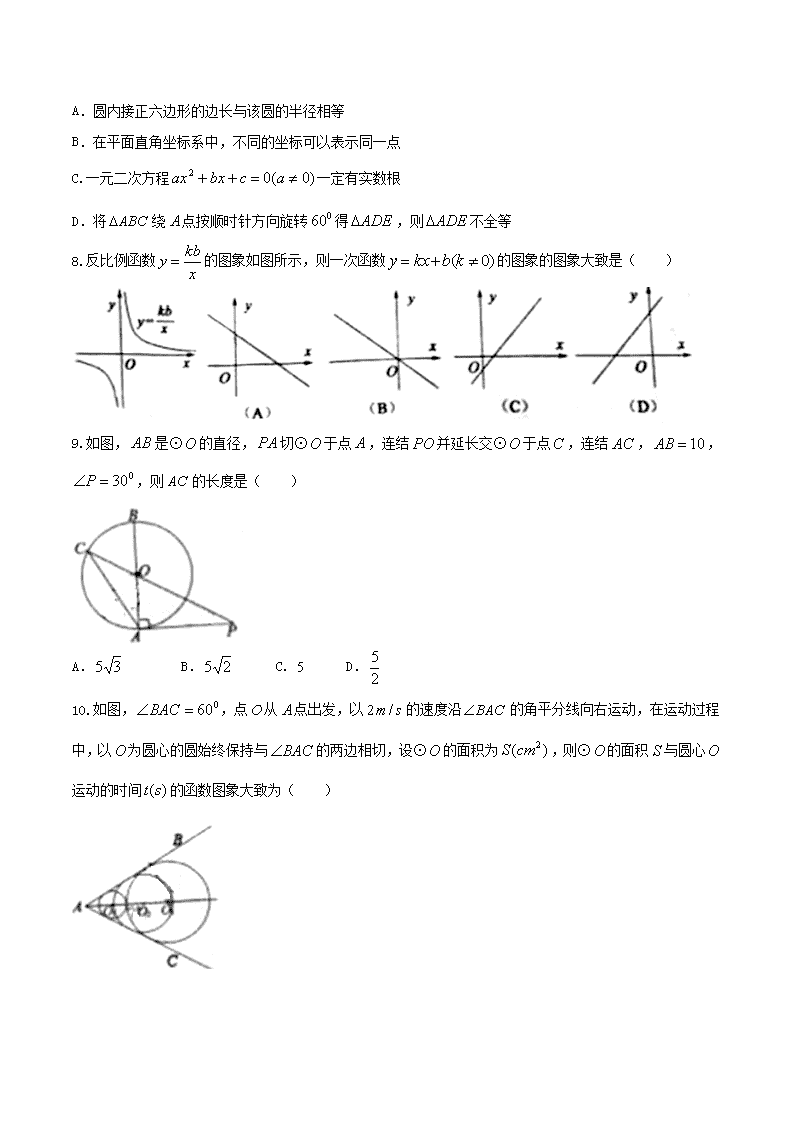
‎2017年山东省日照市学业水平考试 数学试题 一、选择题：‎ ‎1.的绝对值是（ ）‎ A． B．3 C． D．‎ ‎2.剪纸是我国传统的民间艺术.下列剪纸作品既不是中心对称图形，也不是轴对称图形的是（ ）‎ A B C D ‎ ‎3.铁路部门消息：2017年“端午节”小长假期间，全国铁路客流量达到4640万人次.4640万用科学记数法表示为（ ）‎ A． B． C． D．‎ ‎4.在中，，，，则的值为（ ）‎ A． B． C． D．‎ ‎5.如图，，直线交于点，交于点，若，则等于（ ）‎ A． B． C． D．‎ ‎6.式子有意义，则实数的取值范围是（ ）‎ A． B． C. 且 D．‎ ‎7.下列说法正确的是（ ）‎ A．圆内接正六边形的边长与该圆的半径相等 ‎ B．在平面直角坐标系中，不同的坐标可以表示同一点 ‎ C.一元二次方程一定有实数根 ‎ D．将绕点按顺时针方向旋转得，则不全等 ‎8.反比例函数的图象如图所示，则一次函数的图象的图象大致是（ ）‎ ‎9.如图，是⊙的直径，切⊙于点，连结并延长交⊙于点，连结，，，则的长度是（ ）‎ A． B． C. 5 D．‎ ‎10.如图，，点从点出发，以的速度沿的角平分线向右运动，在运动过程中，以为圆心的圆始终保持与的两边相切，设⊙的面积为，则⊙的面积与圆心运动的时间的函数图象大致为（ ）‎ ‎11.观察下面“品”字形中各数之间的规律，根据观察到的规律得出的值为（ ）‎ A．23 B．75 C. 77 D．139‎ ‎12.已知抛物线的对称轴为直线，与轴的一个交点坐标为，其部分图象如图所示，向量结论：‎ ‎①抛物线过原点；‎ ‎②；‎ ‎③‎ ‎④抛物线的顶点坐标为；‎ ‎⑤当时，随增大而增大.‎ 其中结论正确的是（ ）‎ A．①②③ B．③④⑤ C. ①②④ D．①④⑤‎ 二、填空题 ‎13.分解因式： ．‎ ‎14.为了解某初级中学附近路口的汽车流量，交通管理部门调查了某周一至周五下午放学时间段通过该路口的汽车数量（单位：辆），结果如下：‎ ‎183 191 169 190 177‎ 则在该时间段中，通过这个路口的汽车数量的平均数是 ．‎ ‎15. 如图，四边形中，，，以点为圆心，为半径的圆弧与交于点，四边形是平行四边形，，则扇形（图中阴影部分）的面积是 .‎ ‎16.如图，在平面直角坐标系中，经过点的双曲线同时经过点，且点在点的左侧，点的横坐标为，，则的值为 .‎ 三、解答题 ‎ ‎17.（1）计算：；‎ ‎（2）先化简，再求值：，其中.‎ ‎18.如图，已知，，，垂足为.‎ ‎（1）求证：≌； ‎ ‎（2）只需添加一个条件，即 ，可使四边形为矩形.请加以证明.‎ ‎19.若是一个两位正整数，且的个位数字大于十位数字，则称为“两位递增数”（如13,35,56等）.在某次数学趣味活动中，每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数，且只能抽取一次.‎ ‎（1）写出所有个位数字是5的“两位递增数”；‎ ‎（2）请用列表法或树状图，求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率.‎ ‎20.某市为创建全国文明城市，开展“美化绿化城市”活动，计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后，实际每年绿化面积是原计划的1.6倍，这样可提前4年完成任务.‎ ‎（1）问实际每年绿化面积多少万平方米？ ‎ ‎（2）为加大创城力度，市政府决定从2016年起加快绿化速度，要求不超过2年完成，那么实际平均每年绿化面积至少还要增加多少万平方米？‎ ‎21.阅读材料：‎ 在平面直角坐标系中，点到直线的距离公式为：.‎ 例如：求点到直线的距离.‎ 解：由直线知，，，，‎ ‎∴点到直线的距离为.‎ 根据以上材料，解决下列问题：‎ 问题1：点到直线的距离为 ；‎ 问题2：已知：⊙是以点为圆心，1为半径的圆，⊙与直线相切，求实数的值；‎ 问题3：如图，设点为问题2中⊙上的任意一点，点为直线上的两点，且 ‎，请求出的最大值和最小值.‎ ‎22.如图所示，在平面直角坐标系中，⊙经过坐标原点，且与轴，轴分别相交于两点.已知抛物线开口向上，与⊙交于三点，为抛物线的顶点，抛物线的对称轴经过点且垂直轴于点.‎ ‎（1）求线段的长及顶点的坐标； ‎ ‎（2）求抛物线的函数表达式；‎ ‎（3）设抛物线交轴于两点，在抛物线上是否存在点，使得，且∽成立，若存在，请求出点的坐标；若不存在，请说明理由.‎