2014年1月宝山中考数学一模试题 9页

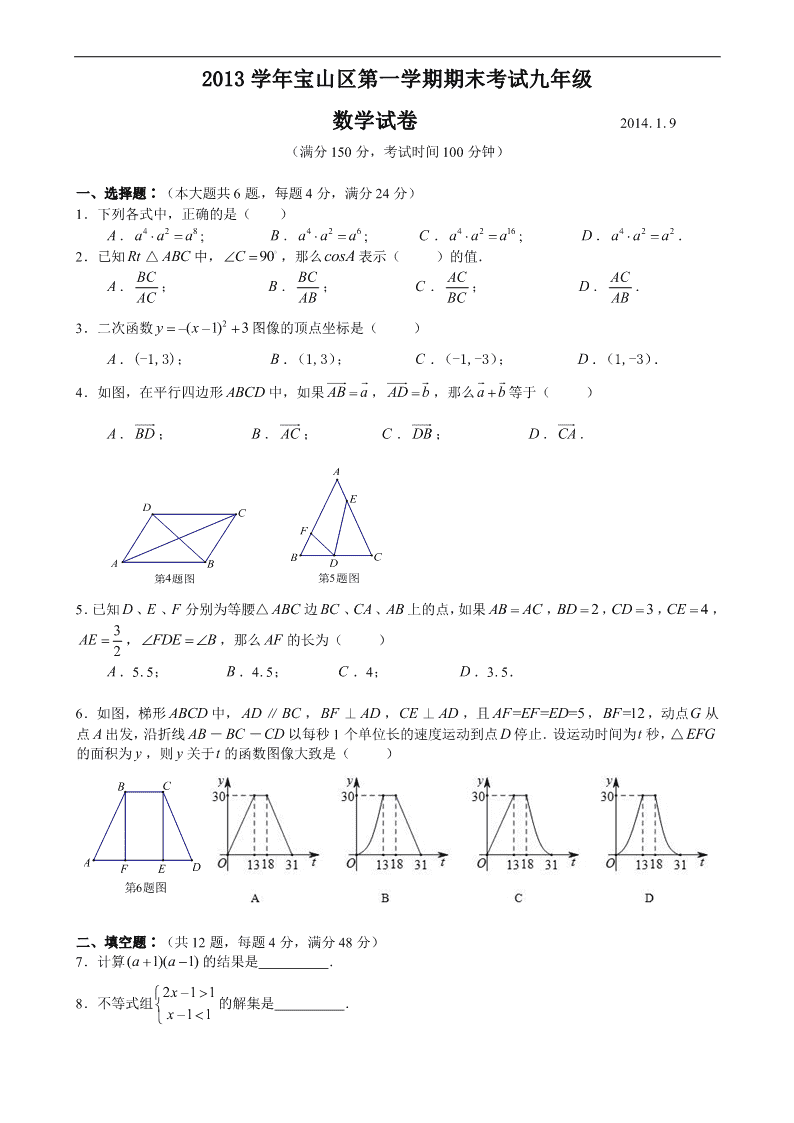
2013 学年宝山区第一学期期末考试九年级 数学试卷 2014.1.9 （满分 150 分，考试时间 100 分钟） 一、选择题∶（本大题共 6 题，每题 4 分，满分 24 分） 1．下列各式中，正确的是（ ） A． 4 2 8a a a; B ． 4 2 6a a a; C． 4 2 16a a a ; D ． 4 2 2a a a． 2．已知 Rt △ ABC 中， 90C ，那么cosA 表示（ ）的值． ． BC AC ； ． BC AB ； ． AC BC ； ． AC AB ． 3．二次函数 2( 1) 3yx    图像的顶点坐标是（ ） ．(-1,3)； ．（1,3）； ．（-1,-3）； ．（1,-3）． 4．如图，在平行四边形 ABCD 中，如果 AB a ， AD b ，那么 ab 等于（ ） ． BD ； ． AC ； ． DB ； ．CA． 第4题图 D A C B 第5题图 A B C F D E 5．已知 D 、E 、F 分别为等腰△ ABC 边 BC 、CA、AB 上的点，如果 AB AC ， 2BD  ， 3CD  ， 4CE  ， 3 2AE  ， FDE B   ，那么 AF 的长为（ ） ．5.5； ．4.5； ．4； ．3.5． 6．如图，梯形 中， AD ∥ BC ， BF ⊥ AD ，CE ⊥ ，且 = = =5AF EF ED ， =12BF ，动点G 从 点 A出发，沿折线 AB － BC －CD 以每秒 1 个单位长的速度运动到点 D 停止．设运动时间为t 秒，△ EFG 的面积为 y ，则 关于 的函数图像大致是（ ） 第6题图 B A C DF E 二、填空题∶（共 12 题，每题 4 分，满分 48 分） 7．计算 ( 1)( 1)aa的结果是 ． 8．不等式组 2 1 1 11 x x    的解集是 ． 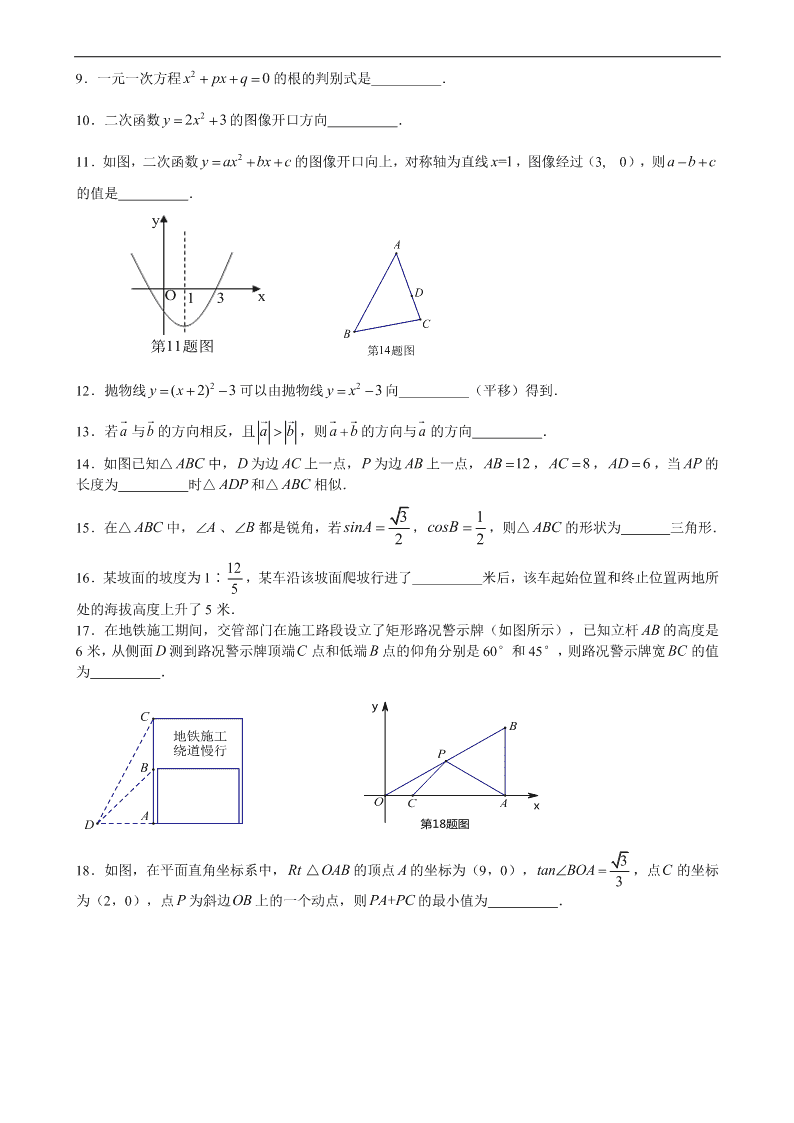9．一元一次方程 2 0x px q   的根的判别式是 ． 10．二次函数 223yx的图像开口方向 ． 11．如图，二次函数 2y ax bx c   的图像开口向上，对称轴为直线 =1x ，图像经过（3, 0），则 a b c 的值是 ． 第11题图 O y x31 第14题图 A B C D 12．抛物线 2( 2) 3yx   可以由抛物线 2 3yx向 （平移）得到． 13．若 a 与b 的方向相反，且 ab ，则 ab 的方向与 的方向 ． 14．如图已知△ ABC 中，D 为边 AC 上一点，P 为边 AB 上一点， 12AB  ， 8AC  ， 6AD  ，当 AP 的 长度为 时△ ADP 和△ 相似． 15．在△ 中， A 、 B 都是锐角，若 3 2sinA  ， 1 2cosB  ，则△ 的形状为 三角形． 16．某坡面的坡度为 1∶12 5 ，某车沿该坡面爬坡行进了 米后，该车起始位置和终止位置两地所 处的海拔高度上升了 5 米． 17．在地铁施工期间，交管部门在施工路段设立了矩形路况警示牌（如图所示），已知立杆 AB 的高度是 6 米，从侧面 测到路况警示牌顶端C 点和低端 B 点的仰角分别是 60°和 45°，则路况警示牌宽 BC 的值 为 ． 地铁施工 绕道慢行 C AD B 第18题图 y xO B A P C 18．如图，在平面直角坐标系中， Rt △OAB 的顶点 A 的坐标为（9，0）， 3 3tan BOA，点C 的坐标 为（2，0），点 P 为斜边OB 上的一个动点，则 +PA PC 的最小值为 ． 三、解答题∶（共 8 题，第 19—22 题每题 8 分；第 23、24 题每题 10 分；第 25 题 12 分；第 26 题 14 分， 共 78 分） 19．（本题满分 8 分） 化简并求值： 2 1 1 2()24x x x ，其中 2 45 45x cos tan． 20．（本题 4+4=8 分） 已知一个二次函数的顶点 A 的坐标为（1，0），且图像经过点 B （2，3）． （1）求这个二次函数的解析式. （2）设图像与 y 轴的交点为C ，记 =OA a ，试用 a 表示OC OB （直接写出答案）． 21．（本题 4+4=8 分） 已知抛物线 1l ： 2 23y x x    和抛物线 2l ： 2 23y x x   相交于 、 ，其中 点的横坐标比 点 的横坐标大． （1）求 、 两点的坐标. （2）射线OA 与 x 轴正方向所相交成的角的正弦值． 22．（本题满分 8 分） 如图已知： AD AB BD AE AC CE，求证： =ABC ADE． A D C E B 23．（本题满分 4+2+4=10 分） 通过锐角三角比的学习，我们已经知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯 一确定，因此边长比与角的大小之间可以相互转化．类似的我们可以在等腰三角形中建立边角之间的联系. 我们定义：等腰三角形中底边与腰的比叫做顶角的正对（ sad ）．如下图在△ ABC 中，AB AC ，顶角 A 的正对记作 sadA ，这时 ==BCsad A AB 底边 腰 . 我们容易知道一个角的大小与这个角的正对值也是互相唯一 确定的．根据上述角的正对定义，解下列问题： （1） 60 =sad _____________； 90 =sad _____________； （2）对于0 180A ， A 的正对值 的取值范围是_____________； （3）试求 36sad 的值． A B C 24．（本题满分 6+4=10 分） 如图 E 为正方形 ABCD 边 BC 延长线上一点， AE 交 DC 于 F ， FG ∥ BE 交 DE 于G ． （1）求证： FG FC ； （2）若 1FG  ， 3AD  ，求tan GFE 的值． F A B D C E G 25、（4+3+2+3=12 分） 如图，已知抛物线 21 44y x bx    与 x 轴相交于 A 、B 两点，与 y 轴相交于点C ，若已知 点的坐 标为 （8，0）． （1）求抛物线的解析式及其对称轴方程； （2）连接 AC 、 BC ，试判断△ AOC 与△ COB 是否相似？并说明理由； （3） M 为抛物线上 之间的一点， N 为线段 上的一点，若 MN ∥ 轴，求 MN 的最大值； （4）在抛物线的对称轴上是否存在点Q ，使△ ACQ 为等腰三角形？若存在，求出符合条件的Q 点坐标； 若不存在，请说明理由． y xA B C O 26．（本题 6+8=14 分） 如图△ ABC 中， =C 90°， =A 30°， 5BC cm ；在△ DEF 中， =D 90°， =E 45°， 3DE cm ．现 将△ 的直角边 DF 与△ 的斜边 AB 重合在一起，并将△ 沿 方向移动（如图）．在移动 过程中， D 、 F 两点始终在 边上（移动开始时点 与点 A 重合，一直移动至点 与点 B 重合为止）． （1）在△ 沿 方向移动的过程中，有人发现： E 、 两点间的距离随 AD 的变化而变化，现设 AD x ， BE y ，请你写出 y 与 x 之间的函数关系式及其定义域； （2）请你进一步研究如下问题∶ 问题①∶当△ 移动至什么位置，即 的长为多少时， 、 的连线与 AC 平行？ 问题②∶在△ 的移动过程中，是否存在某个位置，使得 22.5EBD ？如果存在，求出 的长度； 如果不存在，请说明理由； 问题③∶当△ 移动至什么位置，即 的长为多少时，以线段 、 EB 、 BC 的长度为三边长的三 角形是直角三角形？ A C B E D F 2013 学年宝山区第一学期期末考试九年级 数学试卷答案与评分标准 一、选择题∶ 1． B ． 2． D ． 3． ． 4． ． 5． ． 6． A ． 二、填空题∶ 7． 2 1a  ． 8．12x． 9． 2 4pq ． 10．向上． 11．0． 12．左移两个单位． 13．相同． 14．4 或 9． 15．等边． 16．13． 17．6 3 6 ． 18． 67 ． 三、解答题∶ 19．解：原式       2 2 2 22 x x x x xx     2x x  将 2 45 45 2 1x cos tan    代入，原式 213 2 2 21     ． 20．解：（1）根据题意设抛物线解析式为    210y a x a   ． 将 B 点坐标（2,3）代入得： 3a  ． ∴该抛物线解析式为  231yx． （2）易得∶  0,3C ． ∴ 2OC OB BC a    ． 21．解：（1）根据题意得∶ 2 2 23 23 y x x y x x         ． 解得∶ 1 1 3 23 x y    ， 2 2 3 23 x y    ． 由点 比点 B 的横坐标大，得：  3,2 3A ，  3, 2 3B  ． （2）过 A 作 AH ⊥ x 轴于 H ． 易得 23AH  ， 15AO  ． 2 3 2 5 515 AHsin AOH AO    ． 射线OA 与 x 轴正方向所相交成的角的正弦值为 25 5 ． 22．证明：∵ AD AB BD AE AC CE， ∴△ ABD ∽△ ACE ． ∴ =DAB EAC， ∵ =EAB DAB EAB EAC      ， ∴ =DAE BAC． ∵ AD AB AE AC ， ∴△ ADE ∽△ ABC ． ∴ =ABC ADE． 23．解：（1）1,2 2 ； （2）02sadA； （3）作 A 的平分线交边 AC 于 D ． 利用角度证△ ABC ∽△ BCD和 BC BD AD． 5136 2 BCsad sadA AD    ． 24．证明：（1）∵CF ∥ AB ， ∴ CF EF AB EA ． ∵ FG ∥ AD ， ∴ FG EF AD EA ． ∴ CF FG AB AD ． ∵ AB AD ，∴CF FG ． （2）根据题意得∶ 2DF  ． ∴ 2 3 DFtan GFE tan DAF AD     ． 25、解：（1）∵抛物线 21 44y x bx    经过点 B （8，0）， ∴ 3 2b  ． ∴抛物线的解析式为 213442y x x    ． 又∵  221 3 1 25434 2 4 4y x x x        ， ∴对称轴方程为直线 3x  ． （2）△ AOC ∽△COB ． 易得C （0，4）， ( 2,0) , (8,0)AB 在△AOC 和△COB 中， 90AOC BOC     2 , 4 , 8 , OA OCOA OC OB OC OB     ∴△AOC∽△COB （3）∵M 为抛物线 213442y x x    上一点，N 为线段 BC： 1 42yx   上的一点， 22112 ( 4) 444MN x x x       当 4x  时 MN 有最大值 4。 （4）∵抛物线的对称轴方程为 3x  ，可设点 (3, )Qt，则有： 222 4 20 2 5AC     ； 2 2 25 25AQ t t    ， 223 ( 4)CQ t   ①当 AQ=CQ 时，有 2225 ( 4) 9tt    ，解得 10 , (3,0)tQ ②当 AC=AQ 时，有 2225 2 5 , 5tt    ，此方程无实数根，∴此时不能构成等腰三角形； ③当 AC＝CQ 时，有 2(t 4) 9 2 5   ，解得 4 11t  ， ∴Q 点坐标为 23(3,4 11) , (3,4 11)QQ 综上所述，点 Q 的坐标为 1(3,0) ,Q 。 26、（1）∵△ABC 中，∠C＝90°，∠A＝30°，BC＝5，∴AB＝10 AD＝x，BD＝10-x， 2 2 2 20 109 (0 x 7)BE BD DE x x       （2）①当 BE∥AC 时，则∠EBD＝∠A＝30° 3 3 DE BD 3(10 ) 9 , 10 3 3xx     ②当∠EBF＝22.5°时，∵∠EFD＝45°，∴EF＝BF 3 2 10 3 , 7 3 2xx      ③AD＝x， 2 20 109 , 5BE x x BC    当 AD 为斜边时， 2 2 2 2 2, 20 109 25AD BE BC x x x      ，解得 6.7x  ； 当 BE 为斜边时， 2 2 2 2 2, 20 109 25BE AD BC x x x      ，解得 4.2x  ； 当 BC 为斜边时， 2 2 2 2 2, 25 20 109BC BE AD x x x      ，无实数解。