2020九年级数学下册 第三章 圆 8页

课时作业(二十八)‎ ‎[第三章　8　圆内接正多边形]‎ 一、选择题 ‎1．2017·株洲下列圆的内接正多边形中，一条边所对的圆心角最大的图形是(　　)‎ A．正三角形 B．正方形 C．正五边形 D．正六边形 ‎2．2017·滨州若正方形的外接圆半径为2，则其内切圆半径为(　　)‎ A. B．2 C. D．1‎ ‎3．2017·达州以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是(　　)‎ A. B. C. D. ‎4．若正六边形的两条平行边相距‎12 cm，则它的边长为()‎ A．‎6 cm B．‎12 cm C．‎4 cm D. 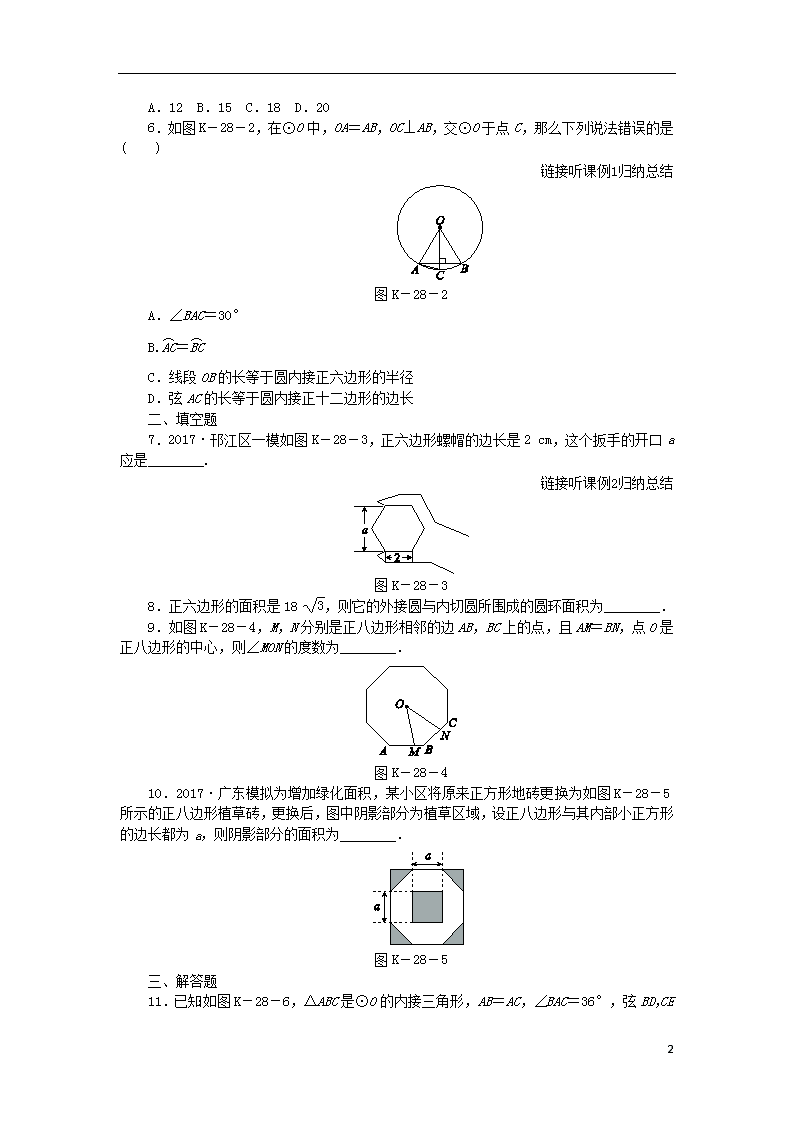cm ‎5．2017·慈溪市期末如图K－28－1，A，B，C三点在⊙O上，AB是⊙O内接正六边形的一边，BC是⊙O内接正十边形的一边，若AC是⊙O内接正n边形的一边，则n等于(　　)‎ 图K－28－1‎ 8‎ A．12 B．‎15 C．18 D．20‎ ‎6．如图K－28－2，在⊙O中，OA＝AB，OC⊥AB，交⊙O于点C，那么下列说法错误的是(　　)‎ ‎　　　　‎ 图K－28－2‎ A．∠BAC＝30°‎ B.＝ C．线段OB的长等于圆内接正六边形的半径 D．弦AC的长等于圆内接正十二边形的边长 二、填空题 ‎7．2017·邗江区一模如图K－28－3，正六边形螺帽的边长是‎2 cm，这个扳手的开口a应是________.‎ 图K－28－3‎ ‎8．正六边形的面积是18 ，则它的外接圆与内切圆所围成的圆环面积为________．‎ ‎9．如图K－28－4，M，N分别是正八边形相邻的边AB，BC上的点，且AM＝BN，点O是正八边形的中心，则∠MON的度数为________．‎ 图K－28－4‎ ‎10．2017·广东模拟为增加绿化面积，某小区将原来正方形地砖更换为如图K－28－5所示的正八边形植草砖，更换后，图中阴影部分为植草区域，设正八边形与其内部小正方形的边长都为a，则阴影部分的面积为________．‎ ‎　‎ 图K－28－5‎ 三、解答题 ‎11．已知：如图K－28－6，△ABC是⊙O的内接三角形，AB＝AC，∠BAC＝36°，弦BD，‎ 8‎ CE分别平分∠ABC，∠ACB.求证：五边形AEBCD是正五边形．‎ 图K－28－6‎ ‎12．2018·平房区二模如图K－28－7，在正六边形ABCDEF中，对角线AE与BF相交于点M，BD与CE相交于点N.‎ ‎(1)求证：AE＝BF；‎ ‎(2)在不添加任何辅助线的情况下，请直接写出图中所有与△ABM全等的三角形．‎ 图K－28－7‎ ‎13．用一个长‎60米的篱笆围成一个羊圈，分别计算所围羊圈是正三角形、正方形、正六边形、圆时的面积(结果精确到1平方米)．‎ ‎(1)比较这些面积的大小；‎ ‎(2)归纳出周长相等的正多边形、圆面积大小的规律(不需证明)．‎ 8‎ 探究题(1)如图K－28－8①所示，M，N分别是⊙O的内接正三角形ABC的边AB，BC上的点，且BM＝CN，连接OM，ON，求∠MON的度数；‎ ‎(2)如图②，③，…，，M，N分别是⊙O的内接正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB，BC上的点，且BM＝CN，连接OM，ON，则图②中∠MON的度数是________，图③中∠MON的度数是________，由此可猜测在图中，∠MON的度数是________．‎ 图K－28－8‎ 8‎ 详解详析 ‎【课时作业】‎ ‎[课堂达标]‎ ‎1．[解析] A　∵正三角形一条边所对的圆心角是360°÷3＝120°，‎ 正方形一条边所对的圆心角是360°÷4＝90°，‎ 正五边形一条边所对的圆心角是360°÷5＝72°，‎ 正六边形一条边所对的圆心角是360°÷6＝60°，‎ ‎∴一条边所对的圆心角最大的图形是正三角形．故选A.‎ ‎2．[解析] A　如图所示，E为切点，连接OA，OE，‎ ‎∵AB是小圆的切线，∴OE⊥AB.∵四边形ABCD是正方形，∴AE＝OE，‎ ‎∴△AOE是等腰直角三角形，‎ ‎∴OE＝OA＝.故选A.‎ ‎3．[解析] A　如图①，‎ ‎∵OC＝2，∴OD＝2×sin30°＝1；‎ 图①‎ 如图②，‎ 图②‎ ‎∵OB＝2，∴OE＝2×sin45°＝；‎ 如图③，‎ 图③‎ ‎∵OA＝2，‎ ‎∴OD＝2×cos30°＝，‎ 则该三角形的三边长分别为1，，.‎ 8‎ ‎∵12＋()2＝()2，‎ ‎∴该三角形是直角三角形，‎ ‎∴该三角形的面积是×1×＝.‎ 故选A.‎ ‎4．[解析] C　两条平行边相距‎12 cm，即可得边心距为‎6 cm，从而可得正六边形的边长为‎4 cm.‎ ‎5．[解析] B　连接OC，OA，OB，‎ ‎∵AB是⊙O内接正六边形的一边，‎ ‎∴∠AOB＝360°÷6＝60°.‎ ‎∵BC是⊙O内接正十边形的一边，‎ ‎∴∠BOC＝360°÷10＝36°，‎ ‎∴∠AOC＝∠AOB－∠BOC＝60°－36°＝24°，‎ ‎∴n＝360°÷24°＝15.‎ 故选B.‎ ‎6．[解析] A　∵OA＝OB，OA＝AB，∴OA＝AB＝OB，∴△AOB是等边三角形，∴∠AOB＝60°.显然∠BAC＝∠BOC＝∠AOB＝×60°＝15°.故选项A说法错误．∵OC⊥AB，∴＝，故选项B说法正确．易知△AOB为等边三角形，∠AOB＝60°，以AB为一边正好可以构成正六边形，故选项C说法正确．∵OC⊥AB，∴＝，∴∠AOC＝30°，＝12，∴弦AC的长等于圆内接正十二边形的边长，故选项D说法正确．故选A.‎ ‎7．[答案] ‎2 cm ‎[解析] 过正六边形的中心O作一边的垂线，垂足为B，连接OA.‎ 则∠O＝30°，AB＝1 cm，‎ ‎∴OB＝＝ cm，‎ ‎∴a＝2OB＝2 cm.‎ 故答案为2 cm.‎ 8‎ ‎8．[答案] 3π ‎[解析] 如图所示，设正六边形的边长为a，‎ ‎∵正六边形的面积是18 ，‎ ‎∴△OAB的面积是3 ，‎ 即AB·OA·sin60°＝3 ，a2·＝3 ，‎ ‎∴a＝2 ，∴OD＝OA·sin60°＝2 ×＝3，‎ ‎∴S圆环＝S外接圆－S内切圆＝π×(2 )2－π×32＝12π－9π＝3π.‎ ‎9．[答案] 45°‎ ‎[解析] 连接OA，OB，OC.‎ ‎∵正八边形是中心对称图形，‎ ‎∴中心角为360°÷8＝45°，‎ ‎∴∠OAM＝∠OBN＝＝67.5°.‎ ‎∵OA＝OB, ∠OAM＝∠OBN，AM＝BN，‎ ‎∴△OAM≌△OBN，‎ ‎∴∠AOM＝∠BON，‎ ‎∴∠MOB＝∠NOC.‎ ‎∵∠AOC＝∠AOM＋∠MOB＋∠BON＋∠NOC＝90°，‎ ‎∴∠MON＝∠MOB＋∠BON＝(∠AOM＋∠MOB＋∠BON＋∠NOC)＝∠AOC＝45°.‎ ‎10．[答案] ‎2a2‎ ‎[解析] △ABC是等腰直角三角形，且AB＝a，则AC＝BC＝a，‎ 则S△ABC＝AC·BC＝×·＝，中间的正方形的面积是a2，则阴影部分的面积是4×＋a2＝2a2.‎ ‎11．证明：∵AB＝AC，∠BAC＝36°，‎ ‎∴∠ABC＝∠ACB＝72°.‎ ‎∵BD，CE分别平分∠ABC，∠ACB，‎ 8‎ ‎∴∠ABD＝∠DBC＝∠ACE＝∠ECB＝∠BAC＝36°，‎ ‎∴＝＝＝＝，‎ 即点A，E，B，C，D把⊙O五等分，‎ ‎∴五边形AEBCD是正五边形．‎ ‎12．解：(1)证明：∵六边形ABCDEF是正六边形，‎ ‎∴AF＝FE＝BA，∠AFE＝∠BAF.‎ 在△AFE与△BAF中，∵AF＝BA，∠AFE＝∠BAF，FE＝AF，‎ ‎∴△AFE≌△BAF，∴AE＝BF.‎ ‎(2)与△ABM全等的三角形有△DEN，△FEM，△CBN.‎ ‎∵六边形ABCDEF是正六边形，‎ ‎∴AB＝AF＝FE，∠BAF＝∠AFE＝120°，‎ ‎∴∠ABM＝∠FAE＝30°，‎ ‎∴∠BAM＝90°.‎ 同理可得∠DEN＝30°，∠EDN＝90°，‎ ‎∴∠ABM＝∠DEN，∠BAM＝∠EDN.‎ 在△ABM和△DEN中，∵∠BAM＝∠EDN，AB＝DE，∠ABM＝∠DEN，‎ ‎∴△ABM≌△DEN.‎ 同理可证明△FEM≌△ABM，△CBN≌△ABM.‎ ‎13．解：①当所围羊圈是正三角形时，其边长为‎20米，‎ S正三角形＝×20×10 ＝100 ≈173(米2)；‎ ‎②当所围羊圈是正方形时，其边长为15米，‎ S正方形＝152＝225(米2)；‎ ‎③当所围羊圈是正六边形时，其边长为10米，‎ S正六边形＝6××10×＝150 ≈260(米2)；‎ ‎④当所围羊圈是圆形时，其半径为米，‎ S圆＝π·()2＝≈286(米2)．‎ ‎(1)S正三角形