人教版中考数学二轮复习专题练习上函数中的面积问题 42页

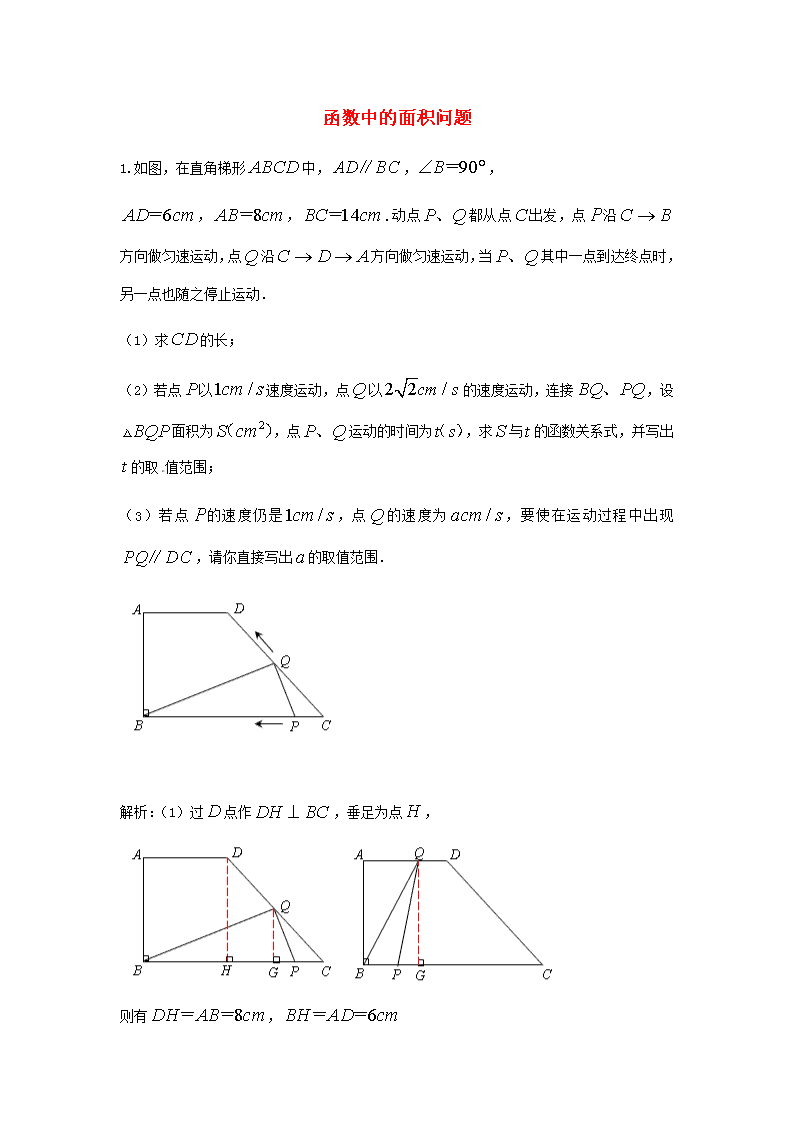
函数中的面积问题 ‎1.如图，在直角梯形中，，，‎ ‎，，.动点都从点出发，点沿方向做匀速运动，点沿方向做匀速运动，当其中一点到达终点时，另一点也随之停止运动．‎ ‎（1）求的长；‎ ‎（2）若点以速度运动，点以的速度运动，连接，设面积为，点运动的时间为，求与的函数关系式，并写出的取值范围；‎ ‎（3）若点的速度仍是，点的速度为，要使在运动过程中出现，请你直接写出的取值范围．‎ 解析：（1）过点作，垂足为点，‎ 则有，‎ ‎∴‎ 在中，．‎ ‎（2）当点运动的时间为，则.‎ ‎①当在上时，过点作，垂足为点，‎ 则由点的速度为，得.‎ 又∵，，‎ ‎∴.‎ ‎∴在中，.‎ 又∵，‎ ‎∴‎ 当运动到点时所需要的时间 ‎∴．‎ ‎②当在上时，过点作，垂足为点，‎ 则，.‎ ‎∴‎ 当运动到点时所需要的时间 ‎∴‎ 综合上述，所求的函数关系式是：.‎ ‎（3）要使运动过程中出现，的取值范围是.‎ ‎2.如图，，点在的两边上，，，连接．点从点出发，以每秒个单位长度的速度沿方向运动，到点停止．当点与两点不重合时，作交于，作于．为射线上一点，且．设点的运动时间为（秒）．‎ ‎（1）用含有的代数式表示的长．‎ ‎（2）求点与点重合时的值．‎ ‎（3）当点在线段上时，设四边形与四边形重叠部分图形的面积为（平方单位）．求与之间的函数关系式．‎ ‎（4）当为某个值时，沿将以为顶点的四边形剪开，得到两个图形，用这两个图形拼成不重叠且无缝隙的图形恰好是三角形．请直接写出所有符合上述条件的值．‎ 解析：（1）由题意知，，四边形为矩形.‎ ‎∴，‎ ‎∴.‎ ‎∵‎ ‎∴‎ ‎（2）由题意知，，‎ ‎∴．‎ ‎∴．‎ 当点与点重合时，，．解得.‎ ‎（3）当点与点重合时，，，得.‎ 当时，如图①，.‎ 当时，如图②，‎ ‎∴与之间的函数关系式为 ‎（4）‎ ‎【分析】‎ ‎（1）由，即可得出比例式从而得出表示的长.‎ ‎（2）根据当点与点重合时，，即可得出答案.‎ ‎（3）分和列出与之间的函数关系式.‎ ‎（4）根据三角形边长相等得出答案：′‎ 如图③，当时，．解得．为拼成的三角形；‎ 如图④，当点与点重合时，．解得．为拼成的三角形；‎ 如图⑤，当时，．解得．为拼成的三角形.‎ ‎3.如图，梯形中，,，于点,，,.从初始时刻开始，动点分别从点同时出发，运动速度均为,动点沿的方向运动，到点停止；动点沿的方向运动，到点停止，设运动时间为，的面积为，（这里规定：线段是面积为的三角形)‎ 解答下列问题：‎ ‎(1)当时，_____;当时，_______ (2)当时，求与之间的函数关系式.‎ ‎(3)当动点在线段上运动时，求出时的值.‎ ‎(4)直接写出在整个运动过程中，使与四边形的对角线平行的所有的值．‎ 解析：（1）；（2）分三种情况：‎ ‎①当时（如图），‎ ‎②当时（如图），‎ ‎③当时（如图），‎ ‎（3）当动点在线段上运动时， ‎ ‎∵，‎ ‎∴，即，解得.‎ ‎∴当时，‎ ‎（4）‎ ‎4.如图，矩形中，，点是的中点，点在的延长线上，且．一动点从点出发，以每秒个单位长度的速度沿匀速运动，到达点后，立即以原速度沿返回；另一动点从点发发，以每秒个单位长度的速度沿射线匀速运动，点同时出发，当两点相遇时停止运动，在点的运动过程中，以为边作等边，使和矩形在射线的同侧．设运动的时间为秒（）．‎ ‎（1）当等边的边恰好经过点时，求运动时间的值；‎ ‎（2）在整个运动过程中，设等边和矩形重叠部分的面积为，请直接写出与之间的函数关系式和相应的自变量的取值范围；‎ ‎（3）设与矩形的对角线的交点为，是否存在这样的，使是等腰三角形？若存大，求出对应的的值；若不存在，请说明理由．‎ 解析：（1）当边恰好经过点时，，，‎ 在中，，，即 解得，即 ‎∴当边恰好经过点时，‎ ‎（2）当时，；‎ 当时，；‎ 当时，；‎ 当时，‎ ‎（3）存在；理由如下：‎ 在中，，∴.‎ 又∵，∴.‎ ‎∴或.‎ ‎1）当时，（如图②），‎ 过点作于，则，‎ 在中，，即，∴，即或 ‎∴或 ‎2）当时，（如图③）‎ 则，又∵，‎ ‎∴，.‎ 又∵，∴，.‎ 即或.‎ ‎∴或.‎ ‎3）当时，（如图④），‎ 则，‎ ‎∴，∴点和点重合.‎ ‎∴，即或，‎ ‎∴（舍去）或.‎ 综上所述，存在个这样的值，使是等腰三角形，即，，，，‎ ‎5.如图，在平行四边形中，，，，一动点从出发以每秒的速度沿的路线匀速运动，过点作直线，使于点，‎ ‎（1）当点运动时，设直线与相交于点，求的面积.‎ ‎（2）当点运动时，另一动点也从出发沿的路线运动，在上以每秒的速度匀速运动，过作直线，使，设点运动的时间为秒（），直线与截平行四边形所得图形的面积为，求关于的函数关系式.‎ 解析：（1）当点运动时，，由 ‎∴‎ ‎∴‎ ‎（2）∵点速度为，点在上的速度为 又，‎ ‎∴‎ ‎∴点在上运动秒钟，而点晚秒钟开始运动 ‎∴点在上运动秒钟 ‎①当时，点与点都在上运动，设与交于点，与交于点，如图②‎ 则 ‎，‎ ‎∴此时两平行线截平行四边形的面积为：‎ ‎②当时，点在运动，点仍在上运动，如图③‎ 设与交于点，与交于点，‎ 则 而 ‎∴‎ ‎③当，点和点都在上运动，如图④‎ 则 ‎∴‎ ‎∴此时两平行线截平行四边形的面积为：‎ ‎∴代入化简得：‎ ‎6.菱形的对角线相交于点，，，动点在线段上从点向点运动，于点，四边形关于对称，四边形与四边形关于对称．设菱形被这两个四边形盖住部分的面积为，未被盖住部分的面积为，．‎ ‎（1）用含的代数式分别表示；‎ ‎（2）若，求的值．‎ 解析：（1）①当点在上时，如图1所示．‎ ‎∵四边形是菱形，，，‎ ‎∴，，，‎ 且．‎ ‎∴．‎ ‎∴．‎ 在中，‎ ‎∵，，，‎ ‎∴．‎ ‎∴．‎ ‎∴．‎ ‎∵四边形关于对称，四边形与四边形关于对称，‎ ‎∴．‎ ‎∴．‎ ‎∴．‎ ‎②当点在上时，如图2所示．‎ ‎∵，，‎ ‎∴．‎ 在中，‎ ‎∵，，．‎ ‎∴．‎ ‎∴．‎ ‎∴‎ ‎．‎ ‎∵四边形关于对称，四边形与四边形关于对称，‎ ‎∴．‎ ‎∴．‎ ‎∴．‎ 综上所述：‎ 当点在上时，，；‎ 当点在上时，，．‎ ‎（2）①当点在上时，．‎ ‎∵，，‎ ‎∴．‎ ‎∴．‎ 解得：，．‎ ‎∵，，‎ ‎∴当点在上时，的情况不存在．‎ ‎②当点在上时，．‎ ‎∵，，‎ ‎∴．‎ ‎∴．‎ 解得：，．‎ ‎∵，，‎ ‎∴．‎ 综上所述：若，则的值为 ‎7.如图，已知矩形的边长，，点是边上的一动点（异于），是边上的任意一点.连、，过作交AQ于，作交于.‎ ‎（1）求证：；‎ ‎（2）设的长为，试求的面积关于的函数关系式，并求当在何处时，取得最大值？最大值为多少？‎ ‎（3）当在何处时，的周长最小？（须给出确定在何处的过程或方法，不必给出证明）‎ 解析：（1）证明：∵，‎ ‎∴‎ ‎∴‎ ‎（2）作中边点的高 ‎∵，‎ ‎∴.‎ ‎∵四边形ABCD是矩形，‎ ‎∴‎ ‎∴‎ ‎∴‎ ‎∴‎ ‎∵，‎ ‎∴，即 ‎∴‎ ‎∵，，‎ ‎∴，即 又∵，，‎ ‎∴，‎ ‎∴‎ ‎∴‎ 又∵，‎ ‎∴，‎ 即.‎ 又∵，，‎ ‎∴四边形是平行四边形 ‎∴.‎ ‎∴‎ 又∵，‎ ‎∴当，即是的中点时，取得最大值.‎ ‎（3）作关于直线的对称点，连交于，则这个点就是使周长最小的点，此时是的中点.‎ ‎8.已知：，都是等边三角形，是与的中点，连接.‎ ‎（1）如图1，当与在同一条直线上时，直接写出与的数量关系和位置关系；‎ ‎（2）固定不动，将图1中的绕点顺时针旋转（）角，如图2所示，判断（1）中的结论是否仍然成立，若成立，请加以证明；若不成立，说明理由；‎ ‎（3）固定不动，将图1中的绕点旋转（）角，作于点．设，线段，，，所围成的图形面积为．当时，求关于的函数关系式，并写出相应的的取值范围．‎ 解析：（1），．‎ ‎（2）证明：连接．‎ 在等边三角形中，为的中点，‎ ‎∴，，．‎ ‎∴．‎ 同理，，．‎ ‎∴，．‎ ‎∴．‎ ‎∴．‎ 延长交于点，交于点．‎ ‎∴，．‎ ‎∴．‎ ‎∴．‎ ‎（3）解：(ⅰ)当绕点顺时针旋转（）角时，‎ ‎∵，‎ ‎∴．‎ ‎∴‎ ‎∴‎ ‎．‎ ‎∴（）．‎ ‎(ⅱ)当绕点逆时针旋转（）角时，可证，‎ ‎∴．‎ ‎∴．‎ ‎∴‎ ‎．‎ ‎∴（)．‎ 综上，（)．‎ ‎9.如图，在中，，，点在射线上，交射线于点，点在的延长线上，且，以为邻边作，连接．‎ ‎（1）当时，求的面积；‎ ‎（2）设，与重叠部分的面积为，求与的函数关系式；‎ ‎（3）当点在线段上时，若是等腰三角形，求的长．‎ 解析：（1）作于 在中，，‎ ‎∴，‎ ‎∴‎ ‎∵，‎ ‎∴‎ ‎∴‎ ‎∵，，‎ ‎∴‎ ‎∵，‎ ‎∴，‎ ‎∴‎ ‎∴‎ ‎（2）设交于点 ‎∵，‎ ‎∴‎ ‎∵，‎ ‎∴，‎ ‎∵‎ ‎①当点在线段上时 ‎∴‎ ‎②当点在延长线上时，则 ‎∴‎ 综合得：‎ ‎（3）∵，‎ ‎∴‎ ‎∵，‎ ‎∴‎ ‎∴‎ 作于，于 在中，‎ ‎，，‎ ‎∴，，‎ ‎∴‎ ‎∴‎ 在中，，‎ ‎①若，则，解得 ‎②若，则 解得（舍去），‎ 综上所述，若是等腰三角形，的长为或 ‎10.已知：如图①，在平行四边形中，，．以为斜边在平行四边形的内部作，，．‎ ‎（1）求的周长；‎ ‎（2）若以每秒个单位长度的速度沿向右平行移动，得到，当与重合时停止移动．设移动时间为秒，与重叠部分的面积为，请直接写出与之间的函数关系式，并写出的取值范围；‎ ‎（3）如图②，在（2）中，当停止移动后得到，将饶点按顺时针方向旋转，在旋转过程中，的对应点为，的对应点为，设直线与直线交于点、与直线交于点．是否存在这样的，使为等腰三角形？若存在，求出的度数；若不存在，请说明理由．‎ 解析：（1）在中，‎ ‎∴，‎ ‎∴的周长为 ‎（2）‎ ‎（3）存在，使为等腰三角形 理由如下：经探究，得 故当为等腰三角形时，也为等腰三角形 ‎①当时（如答图①）‎ 则，∴‎ 即，∴‎ ‎②当时，则 若点在线段的延长线上时（如答图②）‎ ‎∵，‎ ‎∴‎ 即 若点在线段的延长线上时（如答图③）‎ ‎∵，‎ ‎∴，‎ ‎∴‎ ‎∴‎ ‎③当时（如答图④），‎ 则 ‎∵，∴‎ 又∵点在直线上，‎ ‎∴点与点重合 此时三点不能构成三角形 综上所述，的度数为或或时，为等腰三角形 ‎11.如图1，在梯形中，，，，，‎ ‎，边长为的正方形的边在直线上，且与重合，并沿直线以每秒个单位长度的速度向右运动，当与重合时停止运动，设运动时间为秒．‎ ‎（1）当正方形的顶点分别落在线段和上时，求运动时间和的值；‎ ‎（2）在整个运动过程中，设正方形与重合部分的面积为，直接写出与之间的函数关系式和自变量的取值范围；‎ ‎（3）如图2，将沿翻折，得到，取的中点，连接、、，是否存在某一时刻，使是直角三角形，若存在，求出相应的值；若不存在，请说明理由．‎ 解析：（1）当点落在线段上时，设交于，‎ 则 ‎∴，即 ‎∴‎ 当点落在线段上时过作于，‎ 则 ‎∵，∴‎ ‎∴‎ ‎∴，即 ‎∴‎ ‎（2）‎ ‎（3）连接，过作于 由面积法可得 易证，得，‎ ‎①若 过作的平行线，作于，于 易证，∴‎ ‎∴，解得 ‎②若 作于，于 易证，∴‎ ‎∴，解得 ‎③若 过作的平行线，作于，于 易证，∴‎ ‎，解得 综上所述，存在时刻，使是直角三角形 或或或 ‎12.已知，在矩形中，为边上一点，，，，为线段上一点，，连接．如图①，现有一张硬质纸片，，，，斜边与边在同一直线上，点与点重合，点在线段上．如图②，从图①的位置出发，以每秒个单位的速度沿向点匀速移动，同时，点从点出发，以每秒个单位的速度沿向点匀速移动，点为直线与线段的交点，连接．当点到达终点时，和点同时停止运动．设运动时间为秒，解答下列问题：‎ ‎（1）在整个运动过程中，当点在线段上时，求的值．‎ ‎（2）在整个运动过程中，是否存在点，使是等腰三角形．若存在，求出的值；若不存在，说明理由．‎ ‎（3）在整个运动过程中，设与重叠部分的面积为，请直接写出与之间的函数关系式以及自变量的取值范围．‎ 解析：（1）在中，，‎ 由勾股定理，得.‎ ‎∵，,‎ ‎∴，‎ ‎∴当点运动到上时，点与点重合，运动路程为，‎ 又∵运动速度为每秒一个单位长度，‎ ‎∴.‎ ‎（2）存在满足条件的．理由如下：‎ 在中，，‎ 由勾股定理，得：.‎ 由（1）可知，，‎ ‎∴，‎ ‎∴，‎ ‎∴，‎ 又∵，‎ ‎∴‎ ‎∴，即，‎ ‎∴,‎ ‎∴.‎ ‎①当时，如图①，过点作于点，得.‎ 由，得，即，解得.‎ ‎②当时，如图②，由，解得.‎ ‎③当时，如图③，过点作于，可得.‎ 由，得，即，解得.‎ 综上所述，当或或时，△APQ是等腰三角形．‎ ‎（3）‎ 当时，重合部分是一个直角三角形，其斜边长为，两直角边分别长为和，；‎ 当时，重合部分是一个四边形，如图①所示，设与交于点，则是一个等腰三角形，底边，作于点，则，由，可得高，‎ ‎∴的面积为．‎ ‎∴；‎ 当时，重合部分是一个四边形，此时点在内部，如图②所示，；‎ 当时，重合部分是一个三角形，此时点在内部，‎ ‎，，‎ 此时，而的面积为，‎ ‎∴，‎ ‎∴．‎