2019浙江温州中考数学试题 19页

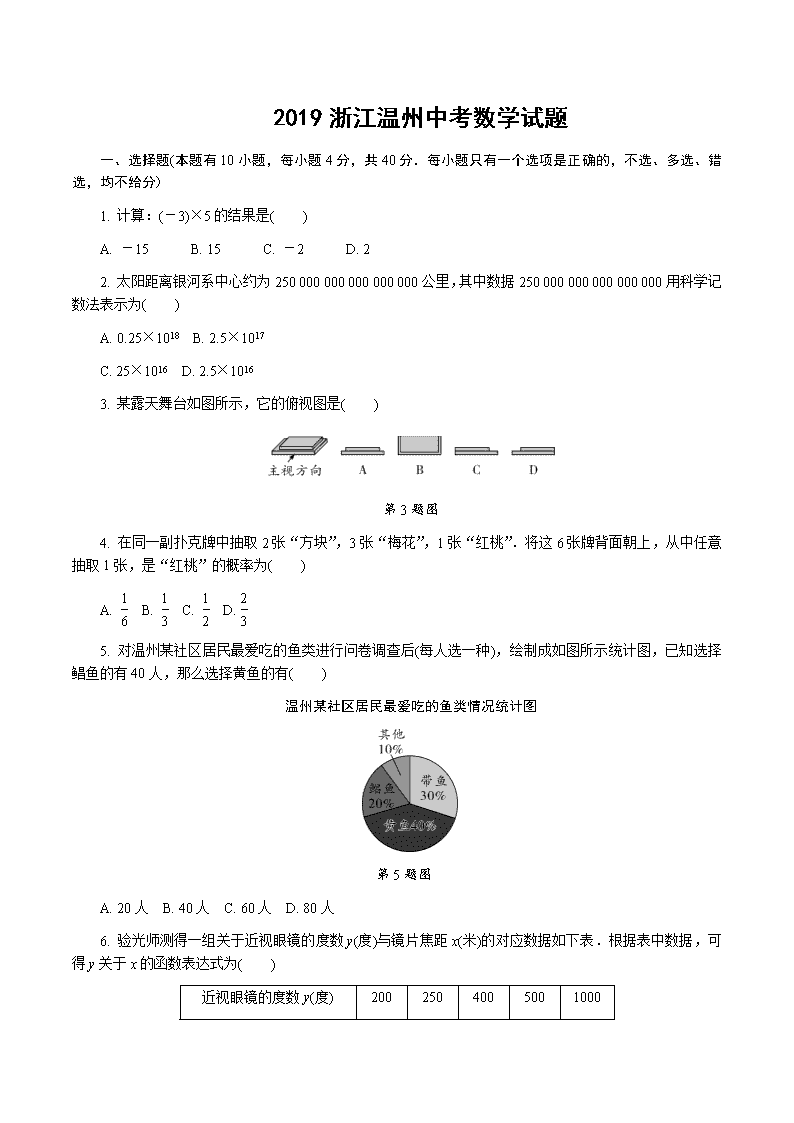
‎2019浙江温州中考数学试题 一、选择题(本题有10小题，每小题4分，共40分．每小题只有一个选项是正确的，不选、多选、错选，均不给分)‎ ‎1. 计算：(－3)×5的结果是(　　)‎ A. －15　　　B. 15　　　C. －2　　　D. 2‎ ‎2. 太阳距离银河系中心约为250 000 000 000 000 000公里，其中数据250 000 000 000 000 000用科学记数法表示为(　　)‎ A. 0.25×1018 B. 2.5×1017‎ C. 25×1016 D. 2.5×1016‎ ‎3. 某露天舞台如图所示，它的俯视图是(　　)‎ 第3题图 ‎4. 在同一副扑克牌中抽取2张“方块”，3张“梅花”，1张“红桃”．将这6张牌背面朝上，从中任意抽取1张，是“红桃”的概率为(　　)‎ A. B. C. D. ‎5. 对温州某社区居民最爱吃的鱼类进行问卷调查后(每人选一种)，绘制成如图所示统计图，已知选择鲳鱼的有40人，那么选择黄鱼的有(　　)‎ 温州某社区居民最爱吃的鱼类情况统计图 ‎ 第5题图 A. 20人 B. 40人 C. 60人 D. 80人 ‎6. 验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表．根据表中数据，可得y关于x的函数表达式为(　　)‎ 近视眼镜的度数y(度)‎ ‎200‎ ‎250‎ ‎400‎ ‎500‎ ‎1000‎ 镜片焦距x(米)‎ ‎0.50‎ ‎0.40‎ ‎0.25‎ ‎0.20‎ ‎0.10‎ A. y＝ B. y＝ C. y＝ D. y＝ ‎7. 若扇形的圆心角为90°，半径为6，则该扇形的弧长为(　　)‎ A. π B. 2π C. 3π D. 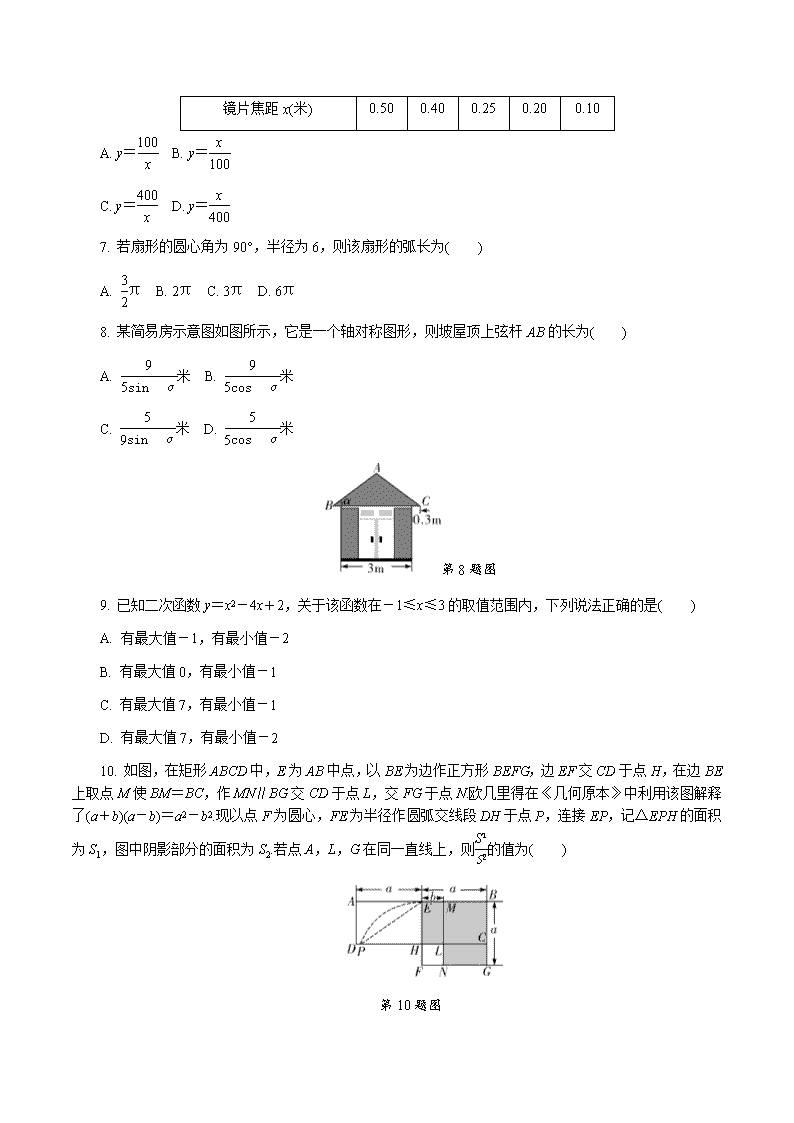6π ‎8. 某简易房示意图如图所示，它是一个轴对称图形，则坡屋顶上弦杆AB的长为(　　)‎ A. 米 B. 米 C. 米 D. 米 第8题图 ‎9. 已知二次函数y＝x2－4x＋2，关于该函数在－1≤x≤3的取值范围内，下列说法正确的是(　　)‎ A. 有最大值－1，有最小值－2‎ B. 有最大值0，有最小值－1‎ C. 有最大值7，有最小值－1‎ D. 有最大值7，有最小值－2‎ ‎10. 如图，在矩形ABCD中，E为AB中点，以BE为边作正方形BEFG，边EF交CD于点H，在边BE上取点M使BM＝BC，作MN∥BG交CD于点L，交FG于点N.欧几里得在《几何原本》中利用该图解释了(a＋b)(a－b)＝a2－b2.现以点F为圆心，FE为半径作圆弧交线段DH于点P，连接EP，记△EPH的面积为S1，图中阴影部分的面积为S2.若点A，L，G在同一直线上，则的值为(　　)‎ ‎　　‎ 第10题图 A. B. C. D. 二、填空题(本题有6小题，每小题5分，共30分)‎ ‎11. 分解因式：m2＋4m＋4＝________．‎ ‎12. 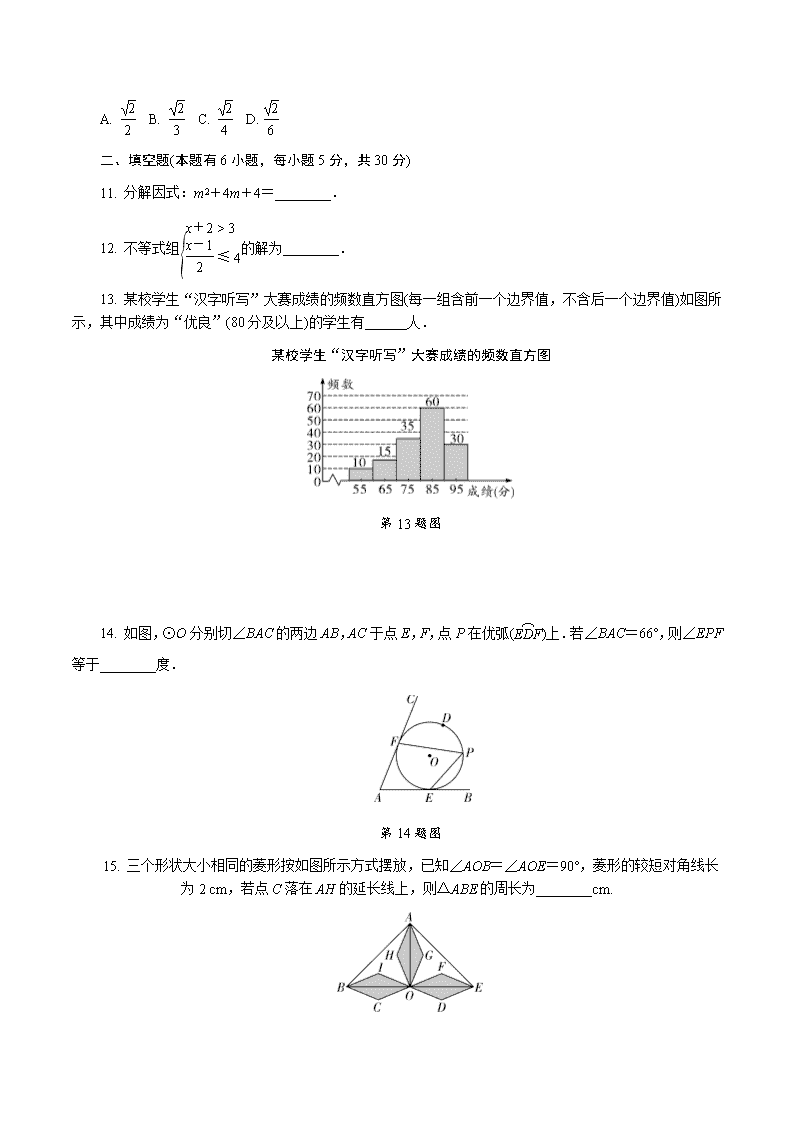不等式组的解为________．‎ ‎13. 某校学生“汉字听写”大赛成绩的频数直方图(每一组含前一个边界值，不含后一个边界值)如图所示，其中成绩为“优良”(80分及以上)的学生有______人．‎ 某校学生“汉字听写”大赛成绩的频数直方图 第13题图 ‎14. 如图，⊙O分别切∠BAC的两边AB，AC于点E，F，点P在优弧()上．若∠BAC＝66°，则∠EPF等于________度．‎ ‎　　‎ 第14题图 ‎15. 三个形状大小相同的菱形按如图所示方式摆放，已知∠AOB＝∠AOE＝90°，菱形的较短对角线长为2 cm，若点C落在AH的延长线上，则△ABE的周长为________cm.‎ 第15题图 ‎16. 图①是一种折叠式晾衣架．晾衣时，该晾衣架左右晾衣臂张开后示意图如图②所示，两支脚OC＝OD＝10分米，展开角∠COD＝60°，晾衣臂OA＝OB＝10分米，晾衣臂支架HG＝FE＝6分米，且HO＝FO＝4分米．当∠AOC＝90°时，点A离地面的距离AM为________分米；当OB从水平状态旋转到OB′(在CO延长线上)时，点E绕点F随之旋转至OB′上的点E′处，则B′E′－BE为________分米．‎ 第16题图 三、解答题(本题有8小题，共80分．解答需写出必要的文字说明、演算步骤或证明过程)‎ ‎17. (本题10分)‎ 计算：(1)|－6|－＋(1－)0－(－3)；‎ ‎(2)－ .‎ ‎18. (本题8分)‎ 如图，在△ABC中，AD是BC边上的中线，E是AB边上一点，过点C作CF∥AB交ED的延长线于点F.‎ ‎(1)求证：△BDE≌△CDF.‎ ‎(2)当AD⊥BC，AE＝1，CF＝2时，求AC的长．‎ 第18题图 ‎19. (本题8分)‎ 车间有20名工人，某一天他们生产的零件个数统计如下表．‎ 车间20名工人某一天生产的零件个数统计表 生产零件的 个数(个)‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎15‎ ‎16‎ ‎19‎ ‎20‎ 工人人数(人)‎ ‎1‎ ‎1‎ ‎6‎ ‎4‎ ‎2‎ ‎2‎ ‎2‎ ‎1‎ ‎1‎ ‎(1)求这一天20名工人生产零件的平均个数．‎ ‎(2)为了提高大多数工人的积极性，管理者准备实行“每天定额生产，超产有奖”的措施．如果你是管理者，从平均数、中位数、众数的角度进行分析，你将如何确定这个“定额”？‎ ‎20. (本题8分)‎ 如图，在7×5的方格纸ABCD中，请按要求画图，且所画格点三角形与格点四边形的顶点均不与点A，B，C，D重合．‎ ‎(1)在图中画一个格点△EFG，使点E，F，G分别落在边AB，BC，CD上，且∠EFG＝90°.‎ ‎(2)在图中画一个格点四边形MNPQ，使点M，N，P，Q分别落在边AB，BC，CD，DA上，且MP＝NQ.‎ 第20题图 ‎21. (本题10分)‎ 如图，在平面直角坐标系中，二次函数y＝－x2＋2x＋6的图象交x轴于点A，B(点A在点B的左侧)．‎ ‎(1)求点A，B的坐标，并根据该函数图象写出y≥0时x的取值范围．‎ ‎(2)把点B向上平移m个单位得点B1.若点B1向左平移n个单位，将与该二次函数图象上的点B2重合；若点B1向左平移(n＋6)个单位，将与该二次函数图象上的点B3重合．已知m>0，n>0，求m，n的值．‎ 第21题图 ‎22. (本题10分)‎ 如图，在△ABC中，∠BAC＝90°，点E在BC边上，且CA＝CE，过A，C，E三点的⊙O交AB于另一点F，作直径AD，连接DE并延长交AB于点G，连接CD，CF.‎ ‎(1)求证：四边形DCFG是平行四边形．‎ ‎(2)当BE＝4，CD＝AB时，求⊙O的直径长．‎ 第22题图 ‎23. (本题12分)‎ 某旅行团32人在景区A游玩，他们由成人、少年和儿童组成．已知儿童10人，‎ 成人比少年多12人．‎ ‎(1)求该旅行团中成人与少年分别是多少人？‎ ‎(2)因时间充裕，该团准备让成人和少年(至少各1名)带领10名儿童去另一景区B游玩，景区B的门票价格为100元/张，成人全票，少年8折，儿童6折，一名成人可以免费携带一名儿童．‎ ‎①若由成人8人和少年5人带队，则所需门票的总费用是多少元？‎ ‎②若剩余经费只有1200元可用于购票，在不超额的前提下，最多可以安排成人和少年共多少人带队？求所有满足条件的方案，并指出哪种方案购票费用最少．‎ ‎24. (本题14分)‎ 如图，在平面直角坐标系中，直线y＝－x＋4分别交x轴、y轴于点B，C，正方形AOCD的顶点D在第二象限内，E是BC中点，OF⊥DE于点F，连接OE.动点P在AO上从点A向终点O匀速运动，同时，动点Q在直线BC上从某一点Q1向终点Q2匀速运动，它们同时到达终点．‎ ‎(1)求点B的坐标和OE的长．‎ ‎(2)设点Q2为(m，n)，当＝tan∠EOF时，求点Q2的坐标．‎ ‎(3)根据(2)的条件，当点P运动到AO中点时，点Q恰好与点C重合．‎ ‎①延长AD交直线BC于点为Q3，当点Q在线段Q2Q3上时，设Q3Q＝s，AP＝t，求s关于t的函数表达式．‎ ‎②当PQ与△OEF的一边平行时，求所有满足条件的AP的长．‎ 第24题图 ‎2019浙江温州中考数学解析 ‎1. A　【解析】原式＝－3×5＝－15.‎ ‎2. B　【解析】将一个大于10的数用科学记数法表示，其形式为a×10n，其中1≤a＜10，n为原数整数位数减1.则250000000000000000＝2.5×1017.‎ ‎3. B　【解析】俯视图是一个几何体由上向下看所得到的视图．从这个几何体的上面看，可得到如选项B所示的图形．‎ ‎4. A　【解析】从6张牌中随机抽取1张，共有6种等可能的情况，其中恰好抽到“红桃”的情况有1种，∴P(恰好抽到红桃)＝.‎ ‎5. D　【解析】∵由扇形统计图可知，选择鲳鱼的占20%，选择黄鱼的占40%，∵选择鲳鱼的有40人，∴总共调查的人数有40÷20%＝200人，∴选择黄鱼的人数有200×40%＝80人．‎ ‎6. A　【解析】根据题意，200×0.5＝100，250×0.4＝100，400×0.25＝100，∴可猜想y关于x的函数表达式是反比例函数，设y＝，则k＝xy＝100，∴y关于x的函数表达式为y＝.‎ ‎7. C　【解析】∵扇形的圆心角为90°，半径为6，∴弧长为＝3π.‎ ‎8. B　【解析】如解图，过点A作AD⊥BC于点D，由轴对称性质可知，BC＝3＋0.3×2＝3.6 m，∴BD＝1.8 m，∵cosα＝，∴AB＝＝＝.‎ 第8题解图 ‎9. D　【解析】∵y＝x2－4x＋2＝(x－2)2－2，∴抛物线的对称轴为x＝2，∵－1＜2＜3，∴当x＝2时抛物线有最小值为－2，当x＝－1时，抛物线有最大值，最大值为(－1－2)2－2＝7.故选D.‎ ‎10. C　【解析】如解图，连接AG，在△ABG中，AB＝2a，BG＝a，∴AB∶BG＝2.∵LC∥AB，∴△LCG∽△ABG，∴LC∶CG＝AB∶BG＝2，∴(a－b)＝2b，‎ 第10题解图 即a＝3b，∴S2＝a2－b2＝8b2，连接PF，则PF＝FE＝a＝3b，在Rt△PFH中，由勾股定理得PH＝＝＝2b，∴S1＝PH·HE＝×2b·2b＝2b2，∴＝＝.‎ ‎11. (m＋2)2　【解析】由完全平方式可知m2＋4m＋4＝(m＋2)2.‎ ‎12. 1＜x≤9　【解析】解不等式x＋2＞3得x＞1，解不等式≤4得x≤9，∴不等式组的解集1＜x≤9.‎ ‎13. 90　【解析】由条形统计图可知，成绩为“优良”(80分及以上)的学生有60＋30＝90人．‎ ‎14. 57　【解析】如解图，连接OE，OF，∵AE，AF分别与⊙O相切于点E，F，∴∠AEO＝∠AFO＝90°，∵四边形内角和为360°，∴∠EAF＋∠EOF＝180°，∵∠BAC＝66°，∴∠EOF＝114°，∴∠EPF＝∠EOF＝57°.‎ 第14题解图 ‎15. 12＋8　【解析】如解图，连接HC，GD，HG，IC，CD，过点O作OM⊥CD，设BO＝OE＝AO＝2b，∴AB＝AE＝2b.由菱形性质可知∠HOA＝∠BOC，∵∠BOA＝90°，∴∠BOH＋∠BOC＝∠BOH＋∠HOA＝90°，∴∠COH＝90°，∴CH＝OH＝AH，∴＝.由菱形对称性可知，HG∥CD，∴△AHG∽△ACD，∴＝，即＝，解得b＝＋1，∴△ABE的周长为2AB＋2BO＝2×2b＋4b＝4×(＋1)＋4×(＋1)＝12＋8.‎ 第15题解图 ‎16. 5＋5；4　【解析】如解图，过点O分别作OK⊥AM，OT⊥CD，垂足分别为K，T，则四边形MTOK是矩形，∴MK＝OT，∵△OCD中OC＝OD，∠COD＝60°，∴△OCD是等边三角形，∴∠OCD＝60°，OT＝OCsin∠OCT＝10sin60°＝5.∵OK∥MC，∴∠KOC＝∠OCT＝60°，∵∠AOC＝90°，∴∠AOK＝30°，∴AK ‎＝AO＝5，∴AM＝AK＋KM＝AK＋OT＝(5＋5)分米．过点F作FN⊥OB于点N，作FR⊥OC于点R，∵∠FON＝∠FOR＝60°，OF＝OF，∠FNO＝∠FRO，∴△FON≌△FOR，∴ON＝OR，FN＝FR，∵FE＝FE′，∴Rt△FEN≌Rt△FE′R，∴E′R＝EN，∵BE＝BO－ON－NE，B′E′＝BO－OE′＝BO－(RE′－OR)＝BO＋OR－RE′，∴B′E′－BE＝(BO＋OR－RE′)－(BO－ON－NE)＝2ON.∵在Rt△ONF中，OF＝4，∠FON＝60°，∴ON＝2，∴B′E′－BE＝4.‎ 第16题解图 ‎17. 解：(1)原式＝6－3＋1＋3＝7；‎ ‎(2)原式＝＝＝.‎ ‎18. (1)证明：∵CF∥AB，‎ ‎∴∠B＝∠FCD，∠BED＝∠F.‎ ‎∵AD是BC边上的中线，∴BD＝CD，‎ 在△BDE与△CDF中，‎ ，‎ ‎∴△BDE≌△CDF(AAS)；‎ ‎(2)解：∵△BDE≌△CDF，∴BE＝CF＝2，‎ ‎∴AB＝AE＋BE＝1＋2＝3.‎ ‎∵AD⊥BC，BD＝CD，‎ ‎∴AC＝AB＝3.‎ ‎19. 解：(1)x＝(9×1＋10×1＋11×6＋12×4＋13×2＋15×2＋16×2＋19×1＋20×1)＝13(个)；‎ 答：这一天20名工人生产零件的平均个数为13个．‎ ‎(2)中位数为12个，众数为11个．‎ 当定额为13个时，有8人达标，6人获奖，不利于提高工人的积极性；‎ 当定额为12个时，有12人达标，8人获奖，不利于提高大多数工人的积极性；‎ 当定额为11个时，有18人达标，12人获奖，有利于提高大多数工人的积极性；‎ ‎∴定额为11个时，有利于提高大多数工人的积极性．‎ ‎20. 解：(1)画法不唯一，如解图①或解图②等；‎ ‎(2)画法不唯一，如解图③或解图④等．‎ 第20题解图 ‎21. 解：(1)令y＝0，则－x2＋2x＋6＝0，‎ ‎∴x1＝－2，x2＝6，‎ ‎∴A(－2，0)，B(6，0)．‎ 由函数图象得，当y≥0时，－2≤x≤6；‎ ‎(2)由题意得B2(6－n，m)，B3(－n，m)，‎ 函数图象的对称轴为直线x＝＝2.‎ ‎∵点B2，B3在二次函数图象上且纵坐标相同，‎ ‎∴＝2.∴n＝1.‎ ‎∴m＝－×(－1)2＋2×(－1)＋6＝.‎ ‎∴m，n的值分别为，1.‎ ‎22. ‎ 第22题解图 ‎(1)证明：如解图，连接AE，‎ ‎∵∠BAC＝90°，‎ ‎∴CF为⊙O的直径．‎ ‎∵AC＝EC，∴CF⊥AE.‎ ‎∵AD为⊙O的直径，‎ ‎∴∠AED＝90°，即GD⊥AE，∴CF∥DG.‎ ‎∵AD为⊙O的直径，‎ ‎∴∠ACD＝90°.∴∠ACD＋∠BAC＝180°.‎ ‎∴AB∥CD.‎ ‎∴四边形DCFG为平行四边形；‎ ‎(2)解：由CD＝AB，可设CD＝3x，AB＝8x，‎ ‎∴CD＝FG＝3x.‎ ‎∵∠AOF＝∠COD，∴AF＝CD＝3x.‎ ‎∴BG＝8x－3x－3x＝2x.‎ ‎∵GE∥CF，‎ ‎∴＝＝.‎ 又∵BE＝4，∴AC＝CE＝6.‎ ‎∴BC＝6＋4＝10.‎ ‎∴AB＝＝8＝8x.‎ ‎∴x＝1.‎ 在Rt△ACF中，AF＝3，AC＝6，‎ ‎∴CF＝＝3，即⊙O的直径长为3.‎ ‎23. 解：(1)设该旅行团中成人x人，少年y人，根据题意，得 ，解得.‎ 答：该旅行团中成人17人，少年5人．‎ ‎(2)①∵成人8人可免费带8名儿童，‎ ‎∴所需门票的总费用为：100×8＋100×0.8×5＋100×0.6×(10－8)＝1320(元)；‎ ‎②设可以安排成人a人、少年b人带队，则1≤a≤17，1≤b≤5.‎ 当10≤a≤17时，‎ ‎(ⅰ)当a＝10时，100×10＋80b≤1200，∴b≤，‎ ‎∴b最大值＝2，此时a＋b＝12，费用为1160元；‎ ‎(ⅱ)当a＝11时，100×11＋80b≤1200，∴b≤，‎ ‎∴b最大值＝1，此时a＋b＝12，费用为1180元；‎ ‎(ⅲ)当a≥12时，100a≥1200，即成人门票至少需要1200元，不合题意，舍去．‎ 当1≤a＜10时，‎ ‎(ⅰ)当a＝9时，100×9＋80b＋60≤1200，∴b≤3，‎ ‎∴b最大值＝3，此时a＋b＝12，费用为1200元；‎ ‎(ⅱ)当a＝8时，100×8＋80b＋2×60≤1200，∴b≤，‎ ‎∴b最大值＝3，此时a＋b＝11＜12.不合题意，舍去；‎ ‎(ⅲ)同理，当a＜8时，a＋b＜12，不合题意，舍去；‎ 综上所述，最多可以安排成人和少年共12人带队，有三个方案：成人10人，少年2人；成人11人，少年1人；成人9人，少年3人；其中当成人10人，少年2人时购票费用最少．‎ ‎24. 解：(1)令y＝0，则－x＋4＝0，‎ ‎∴x＝8，∴B为(8，0)．‎ ‎∴C为(0，4)．‎ 在Rt△BOC中，BC＝＝4.‎ 又∵E为BC中点，‎ ‎∴OE＝BC＝2；‎ 第24题解图①‎ ‎(2)如解图①，作EM⊥OC于点M，DE交y轴于N点，则EM∥CD，‎ ‎∴△CDN∽△MEN，‎ ‎∴＝＝1，‎ ‎∴CN＝MN＝1，‎ ‎∴EN＝＝.‎ ‎∵EN·OF＝ON·EM，‎ ‎∴OF＝＝，‎ 由勾股定理得EF＝，‎ ‎∴tan∠EOF＝＝，∴＝×＝.‎ ‎∵n＝－m＋4，∴m＝6，n＝1，‎ ‎∴Q2为(6，1)；‎ ‎(3)①∵动点P，Q同时作匀速直线运动，‎ ‎∴s关于t成一次函数关系，设s＝kt＋b，‎ 将和代入得，解得，‎ ‎∴s＝t－；‎ 第24题解图②‎ ‎②(ⅰ)当PQ∥OE时(如解图②)，∠QPB＝∠EOB＝∠OBE，‎ 作QH⊥x轴于点H，则PH＝BH＝PB.‎ ‎∵BQ＝6－s＝6－t＋ ‎＝7－t，‎ 又∵cos∠QBH＝＝，‎ ‎∴BH＝14－3t，∴PB＝28－6t，‎ ‎∴t＋28－6t＝12，∴t＝；‎ ‎(ⅱ)当PQ∥OF时(如解图③)，过点Q作QG⊥AQ3于点G，过点P作PH⊥GQ于点H，‎ 由△Q3QG∽△CBO得Q3G∶QG∶Q3Q＝1∶2∶.‎ ‎∵Q3Q＝s＝t－，‎ 第24题解图③‎ ‎∴Q3G＝t－1，QG＝3t－2，‎ ‎∴PH＝AG＝AQ3－Q3G ‎＝6－(t－1)＝7－t，‎ QH＝QG－AP＝3t－2－t＝2t－2.‎ ‎∵∠HPQ＝∠CDN.‎ ‎∴tan∠HPQ＝tan∠CDN＝.‎ ‎∴2t－2＝(7－t)，‎ ‎∴t＝；‎ ‎(ⅲ)由图形可知PQ不可能与EF平行．‎ 综上所述，当PQ与△OEF的一边平行时，AP的长为或.‎