上海市2017中考数学试题 6页

‎2017 年上海市初中毕业统一学业考试 数学试卷 考生注意：‎ ‎1．本试卷共 25 题；‎ ‎2．试卷满分 150 分，考试时间 100 分钟 ‎3．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题 一律无效；‎ ‎4．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明 或计算的主要步骤．‎ 一、选择题：（本大题共 6 题，每题 4 分，满分 24 分）‎ ‎【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答 题纸的相应位置上】‎ ‎1．下列实数中，无理数是 ‎（A） 0 ； （B） 2 ； （C） - 2 ； （D） 2 ．‎ ‎7‎ ‎2．下列方程中，没有实数根的是 ‎（A） x 2 - 2 x = 0 ； （B） x 2 - 2 x - 1 = 0 ；‎ ‎（C） x 2 - 2 x + 1 = 0 ； （D） x 2 - 2 x + 2 = 0 ．‎ ‎3．如果一次函数 y = kx + b （k 、b 是常数，k ¹ 0 ）的图像经过第一、二、四象限，那么k 、b 应满足的条件是 ‎（A） k > 0 ，且 b > 0 ； （B） k < 0 ，且 b > 0 ；‎ ‎（C） k > 0 ，且 b < 0 ； （D） k < 0 ，且 b < 0 ．‎ ‎4．数据 2、5、6、0、6、1、8 的中位数和众数分别是 ‎（A）0 和 6； （B）0 和 8； （C）5 和 6； （D）5 和 8．‎ ‎5．下列图形中，既是轴对称又是中心对称图形的是 ‎（A）菱形； （B）等边三角形； （C）平行四边形； （D）等腰梯形．‎ ‎6．已知平行四边形 ABCD，AC、BD 是它的两条对角线，那么下列条件中，能判断这个 平行四边形为矩形的是 ‎（A）∠BAC=∠DCA； （B）∠BAC=∠DAC；‎ ‎（C）∠BAC=∠ABD； （D）∠BAC=∠ADB．‎ ‎[来源:学科网]‎ 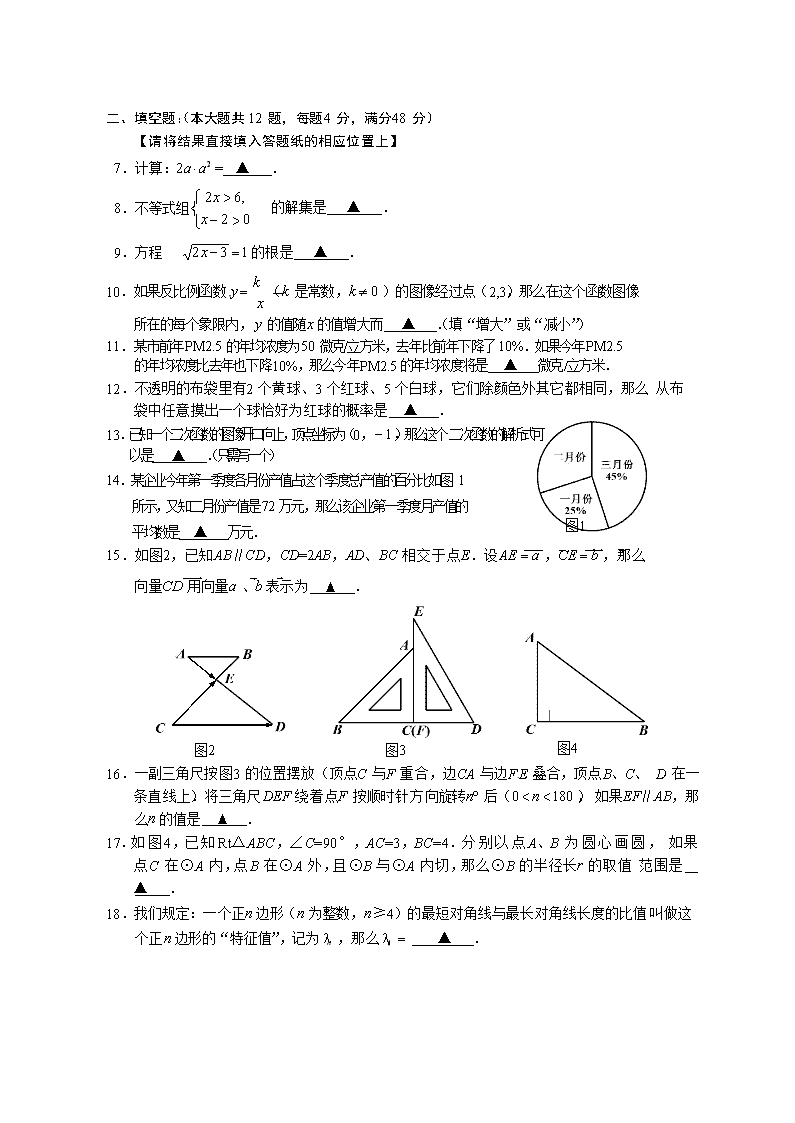二、填空题：（本大题共 12 题，每题 4 分，满分 48 分）‎ ‎【请将结果直接填入答题纸的相应位置上】‎ ‎7．计算： ‎2a × a 2 = ▲ ．‎ ì 2 x > 6,‎ ‎8．不等式组 í îx - 2 > 0‎ ‎的解集是 ▲ ．‎ ‎9．方程 ‎2 x - 3 = 1 的根是 ▲ ．‎ ‎10．如果反比例函数 y = k （ k 是常数， k ¹ 0 ）的图像经过点（2,3），那么在这个函数图像 x 所在的每个象限内， y 的值随 x 的值增大而 ▲ ．（填“增大”或“减小”）‎ ‎11．某市前年 PM2.5 的年均浓度为 50 微克/立方米，去年比前年下降了 10%．如果今年 PM2.5‎ 的年均浓度比去年也下降 10%，那么今年 PM2.5 的年均浓度将是 ▲ 微克/立方米．‎ ‎12．不透明的布袋里有 2 个黄球、3 个红球、5 个白球，它们除颜色外其它都相同，那么 从布袋中任意摸出一个球恰好为红球的概率是 ▲ ．‎ ‎13．已知一个二次函数的图像开口向上，顶点坐标为（0，- 1 ），那么这个 二次函数的解析式可以是 ▲ ．（只需写一个）‎ ‎14．某企业今年第一季度各月份产值占这个季度总产值的百分比如图 1‎ 所示，又知二月份产值是 72 万元，那么该企业第一季度月产值的 平均数是 ▲ 万元． 图 1‎ ‎15．如图 2，已知 AB∥CD，CD=2AB，AD、BC 相交于点 E．设 AE = a ， CE = b ，那么 向量 CD 用向量 a 、 b 表示为 ▲ ．‎ ‎[来源:学科网]‎ 图 2 图 3 图 4‎ ‎16．一副三角尺按图 3 的位置摆放（顶点 C 与 F 重合，边 CA 与边 FE 叠合，顶点 B、C、 D 在一条直线上）．将三角尺 DEF 绕着点 F 按顺时针方向旋转 n° 后（ 0 < n < 180 ）， 如果 EF∥AB，那么 n 的值是 ▲ ．‎ ‎17．如图 4，已知 Rt△ABC ，∠C=90 °，AC=3，BC =4．分别以点 A、B 为圆心画圆， 如果点 C 在⊙A 内，点 B 在⊙A 外，且⊙B 与⊙A 内切，那么⊙B 的半径长 r 的取值 范围是 ▲ ．‎ ‎18．我们规定：一个正 n 边形（ n 为整数， n ≥4）的最短对角线与最长对角线长度的比值 叫做这个正 n 边形的“特征值”，记为ln ，那么l6 = ▲ ．‎ 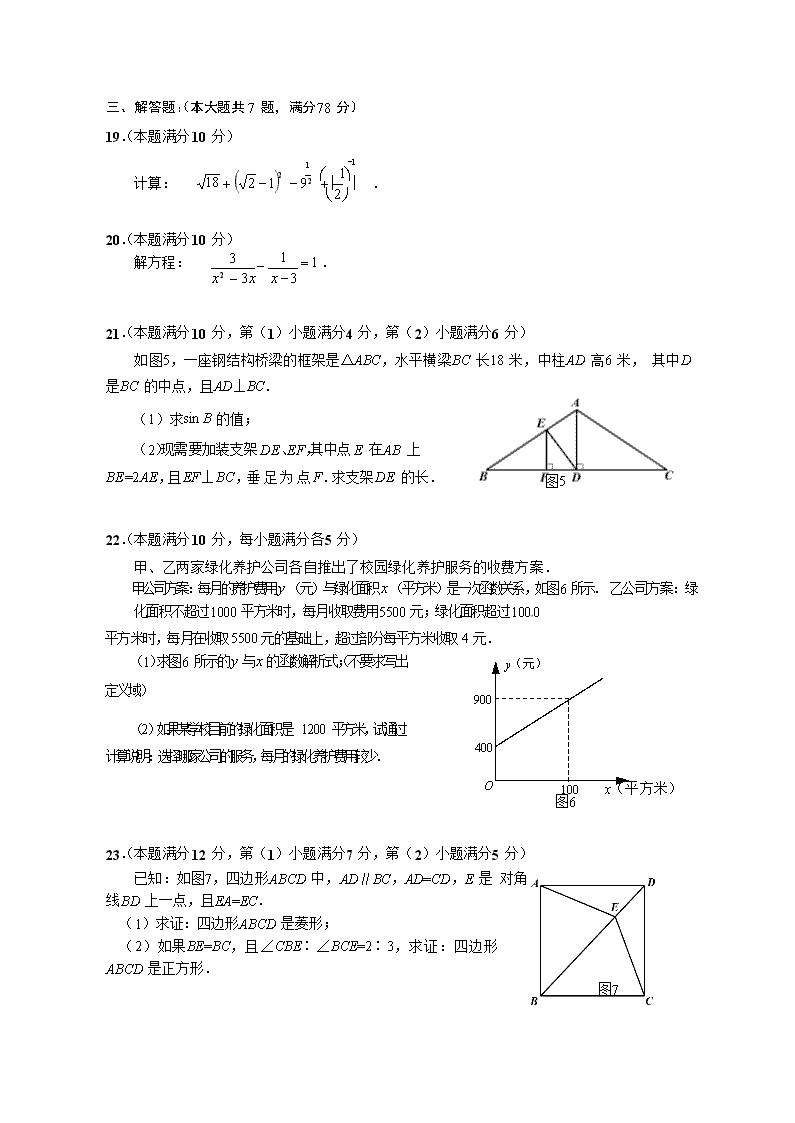三、解答题：（本大题共 7 题，满分 78 分）‎ ‎19．（本题满分 10 分）‎ ‎1‎ -1‎ æ ö 计算：‎ ‎18 + ( ‎2 - 1)2 - 9 2 + ç 1 ÷ ．‎ è 2 ø ‎20．（本题满分 10 分）[来源:Zxxk.Com]‎ 解方程：‎ ‎3 - x 2 - 3x ‎1‎ x - 3‎ ‎‎ = 1 ．‎ ‎21．（本题满分 10 分，第（1）小题满分 4 分，第（2）小题满分 6 分）‎ 如图 5，一座钢结构桥梁的框架是△ABC，水平横梁 BC 长 ‎18 米，中柱 AD 高 ‎6 米， 其中 D 是 BC 的中点，且 AD⊥BC．‎ ‎（1）求 sin B 的值；‎ ‎（2）现需要加装支架 DE 、EF，其中点 E 在 AB 上 BE=2AE，且 EF ⊥BC ，垂足为点 F．求支架 DE 的长． 图 5‎ ‎[来源:学科网ZXXK]‎ ‎22．（本题满分 10 分，每小题满分各 5 分）‎ 甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案．‎ 甲公司方案：每月的养护费用 y （元）与绿化面积 x （平方米）是一次函数关系，如图 6 所示． 乙公司方案：绿化面积不超过 ‎1000 平方米时，每月收取费用 5500 元；绿化面积超过 1000‎ 平方米时，每月在收取 5500 元的基础上，超过部分每平方米收取 4 元．‎ ‎（1）求图 6 所示的 y 与 x 的函数解析式；（不要求写出 定义域）‎ ‎‎ ‎900‎ ‎‎ y（元）[来源:学#科#网Z#X#X#K]‎ ‎（2）如果某学校目前的绿化面积是‎1200 平方米，试通过 计算说明：选择哪家公司的服务，每月的绿化养护费用较少．‎ ‎‎ ‎400‎ O ‎‎ ‎100‎ 图 6‎ ‎‎ x（平方米）‎ ‎23．（本题满分 12 分，第（1）小题满分 7 分，第（2）小题满分 5 分）‎ 已知：如图 7，四边形 ABCD 中，AD∥BC，AD=CD，E 是 对角线 BD 上一点，且 EA=EC．‎ ‎（1）求证：四边形 ABCD 是菱形；‎ ‎（2）如果 BE=BC，且∠CBE∶∠BCE=2∶3，求证：四边形 ABCD 是正方形．‎ 图 7‎ ‎24．（本题满分 12 分，每小题满分各 4 分）‎ 已知在平面直角坐标系 xOy 中（如图 8），已知抛物线 y = - x 2 + bx + c 经过点 A（2,2），对称轴是直线 x = 1 ， y 顶点为 B．‎ ‎（1）求这条抛物线的表达式和点 B 的坐标；‎ ‎（2）点 M 在对称轴上，且位于顶点上方，设它的 1‎ 纵坐标为 m，联结 AM，用含 m 的代数式表示∠ABM O 1 x 的余切值；‎ ‎（3）将该抛物线向上或向下平移，使得新抛物线 的顶点 C 在 x 轴上．原抛物线上一点 P 平移后的对应 点为点 Q，如果 OP=OQ，求点 Q 的坐标． 图 8‎ ‎25．（本题满分 14 分，第（1）小题满分 4 分，第（2）小题满分 5 分，第（3）小题满分 5 分）‎ 如图 9，已知⊙O 的半径长为 1，AB、AC 是⊙O 的两条弦，且 AB=AC，BO 的延长 线交 AC 于点 D，联结 OA、OC．‎ ‎（1）求证：△OAD∽△ABD；‎ ‎（2）当△OCD 是直角三角形时，求 B、C 两点的距离；‎ ‎（3）记△AOB、△AOD、△COD 的面积分别为 S1 、 S2 、 S3 ，如果 S2 是 S1 和 S3 的比例 中项，求 OD 的长．‎ 图 9 备用图