2020九年级数学上册与圆有关的位置关系讲义（新版）新人教版 5页

与圆有关的位置关系（讲义）‎ 与圆有关的位置关系，关键是找 d．和 ．r．‎ Ø 知识点睛 1. 点与圆的位置关系 O C d 表示 的距离，r 表示 ．‎ ‎①点在圆外Û ； A ‎②点在圆上Û ；‎ ‎③点在圆内Û ．‎ 三点定圆定理： ． B O O 注：三角形的三个顶点确定一个圆，这个圆叫做三角形的外接圆，外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心．‎ 2. 直线与圆的位置关系 O d 表示 的距离，r 表示 ．‎ ‎①直线与圆相交Û ；‎ ‎②直线与圆相切Û ；‎ O1O2‎ O2‎ O1‎ ‎③直线与圆相离Û ．‎ 切线的判定定理： ‎ ‎ ； 切线的性质定理： ．‎ O1O2‎ O1‎ O2‎ ‎*切线长定理： ‎ ‎ ． 注：与三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心．‎ O1‎ O2‎ ‎*3. 圆与圆的位置关系 d 表示 的距离，R 表示 ，r 表示 ．‎ ‎①圆与圆外离Û ；‎ ‎②圆与圆外切Û ；‎ ‎③圆与圆内切Û ；‎ ‎④圆与圆内含Û ；‎ ‎⑤圆与圆相交Û ．‎ ‎4. 圆内接正多边形 只要把一个圆分成相等的一些弧，就可以作出这个圆的内接正多边形．‎ ‎ 叫做圆内接正多边形，这个圆叫做该正多边形的 .‎ 正多边形的中心： ；‎ 5‎ 正多边形的半径： ； 正多边形的中心角： ； 正多边形的边心距： ．‎ 5‎ Ø 精讲精练 ‎5‎ 1. 矩形ABCD 中，AB=8，BC = 3‎ ‎‎ ‎，点P 在AB 边上，且BP=3AP，‎ 5‎ 如果圆 P 是以点 P 为圆心，PD 为半径的圆，那么下列判断正确的是（ ）‎ A．点 B，C 均在圆 P 外 B．点 B 在圆 P 外、点 C 在圆 P 内C．点 B 在圆 P 内、点 C 在圆 P 外D．点 B，C 均在圆 P 内 2. 如图，在 5×5 的正方形网格中，一条圆弧经过 A，B，C 三点， 那么这条圆弧所在圆的圆心是点 ．‎ A B C P Q R M ‎② ①‎ ‎③‎ ‎④‎ 第 2 题图 第 3 题图 3. 小明不慎把家里的圆形玻璃打碎了，其中四块碎片如图所示， 为配到与原来大小一样的圆形玻璃，小明带到商店去的一块玻璃碎片应该是（ ）‎ A．第①块 B．第②块 C．第③块 D．第④块 A 4. 如图，在 Rt△ABC 中，∠C=90°，‎ ‎∠A=60°，BC=‎4 cm，以点 C 为圆心，以 ‎3 cm 长为半径作圆，则⊙C 与 AB 的位置关系是 ． C B 5. 在 Rt△ABC 中，∠C=90°，AC=3，BC=4．以 C 为圆心，R 为半径所作的圆与斜边 AB 有且只有一个公共点，则 R 的取值范围是 ．‎ 6. 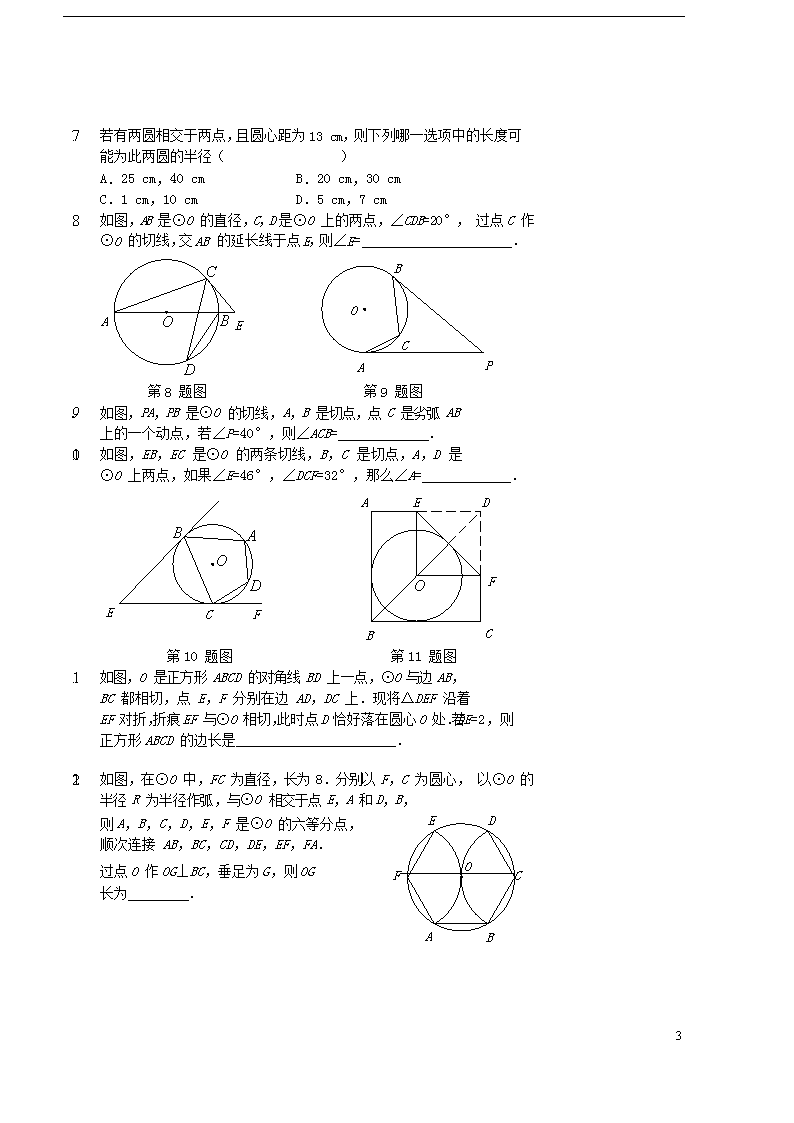在△ABC 中，∠C=90°，AC=‎3 cm，BC=‎4 cm．若⊙A，⊙B 的半径分别为 ‎1 cm，‎4 cm，则⊙A，⊙B 的位置关系是 ．‎ 5‎ 1. 若有两圆相交于两点，且圆心距为 ‎13 cm，则下列哪一选项中的长度可能为此两圆的半径（ ）‎ A．‎25 cm，‎40 cm B．‎20 cm，‎‎30 cm C．‎1 cm，‎10 cm D．‎5 cm，‎‎7 cm 2. 如图，AB 是⊙O 的直径，C，D 是⊙O 上的两点，∠CDB=20°， 过点 C 作⊙O 的切线，交 AB 的延长线于点 E，则∠E= ．‎ C O B D B A E O C A P 第 8 题图 第 9 题图 3. 如图，PA，PB 是⊙O 的切线，A，B 是切点，点 C 是劣弧 AB 上的一个动点，若∠P=40°，则∠ACB= ．‎ 4. 如图，EB，EC 是⊙O 的两条切线，B，C 是切点，A，D 是 ‎⊙O 上两点，如果∠E=46°，∠DCF=32°，那么∠A= ．‎ B A O D O A E D F E C F B C 第 10 题图 第 11 题图 5. 如图，O 是正方形 ABCD 的对角线 BD 上一点，⊙O 与边 AB，‎ BC 都相切，点 E，F 分别在边 AD，DC 上．现将△DEF 沿着 EF 对折，折痕EF 与⊙O 相切，此时点D 恰好落在圆心O 处．若DE=2，则正方形 ABCD 的边长是 ．‎ 6. 如图，在⊙O 中，FC 为直径，长为 8．分别以 F，C 为圆心， 以⊙O 的半径 R 为半径作弧，与⊙O 相交于点 E，A 和 D，B，‎ 则 A，B，C，D，E，F 是⊙O 的六等分点， E D 顺次连接 AB，BC，CD，DE，EF，FA．‎ 过点 O 作 OG⊥BC，垂足为 G，则 OG F O C 长为 ．‎ A B 5‎ 1. 如图，正六边形 ABCDEF 内接于⊙O，半径为 4，则这个正 ‎︵‎ A F O M C D 六边形的边心距 OM 和BC 的长分别为（ ）‎ 5‎ ‎，‎ A． 2 p ‎3‎ ‎B． 2 3 ，p 5‎ ‎3‎ ‎，‎ C． 2p 3‎ ‎D． 2 4p B E ‎3‎ ‎，‎ ‎3‎ 5‎ 2. 如图，⊙O 的直径为 AB，点 C 在圆周上（异于 A，B）， AD⊥CD．‎ ‎（1）若 BC=3，AB=5，求 AC 的长；‎ ‎（2）若 AC 是∠DAB 的平分线，求证：直线 CD 是⊙O 的切线．‎ D C A O B 3. 如图，在△ABC 中，∠C=90°，点 O 在 AC 上，以 OA 为半径的⊙O 交 AB 于点 D，BD 的垂直平分线交 BC 于点 E，交 BD 于点 F，连接 DE．‎ ‎（1）判断直线 DE 与⊙O 的位置关系，并说明理由；‎ ‎（2）若 AC=6，BC=8，OA=2，求线段 DE 的长．‎ C E O A D F B 5‎ ‎【参考答案】‎ Ø 知识点睛 1. 点到圆心；圆的半径； d > r ； d = r ； d < r ． 不在同一条直线上的三个点确定一个圆．‎ 2. 圆心 O 到直线 l；圆的半径； d < r ； d = r ； d > r ． 经过半径的外端且垂直于该半径的直线是圆的切线； 圆的切线垂直于过切点的半径．‎ 从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角．‎ 3. 圆心之间；大圆半径；小圆半径．‎ d > R + r ； d = R + r ； d = R - r ； 0 ≤ d < R - r ；‎ R - r < d < R + r ．‎ 4. 顶点都在同一圆上的正多边形；外接圆．‎ 一个正多边形的外接圆的圆心叫做这个正多边形的中心； 外接圆的半径叫做正多边形的半径；‎ 正多边形每一边所对的圆心角叫做正多边形的中心角； 中心到正多边形的一边的距离叫做正多边形的边心距．‎ Ø 精讲精练 1. C 2. Q 3. B 4. 相交 ‎5. 3 < R ≤ 4 或 R = 12‎ ‎5‎ 6. 外切 7. B ‎8. 50°‎ ‎9. 110°‎ ‎10. 99°‎ ‎2‎ ‎11. 2 + ‎12. 2 3‎ ‎13. D ‎14. （1）AC=4；（2）证明略 ‎15. （1）直线 DE 与⊙O 相切，理由略；（2） DE = 19‎ ‎4‎ 5‎