初中数学中考总复习课件PPT：第25课时 点、直线与圆的位置关系 24页

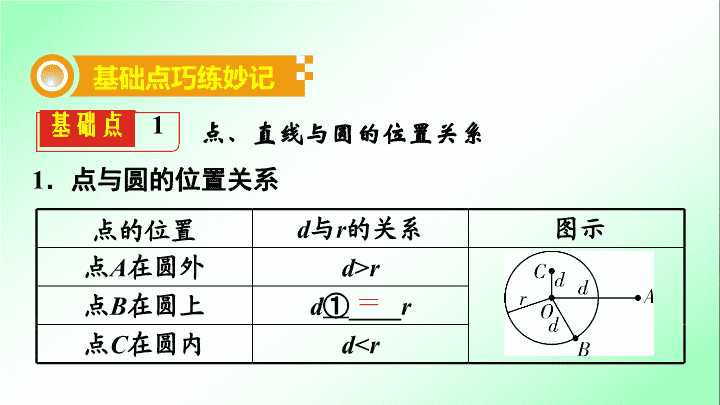
第一部分 夯实基础　提分多 第 六 单元 圆 第 2 5 课时 点、直线与圆的位置关系 基础点 1 点、直线与圆的位置关系 基础点巧练妙记 1 ．点与圆的位置关系 点的位置 d 与 r 的关系 图示 点 A 在圆外 d > r 点 B 在圆上 d ① ____ r 点 C 在圆内 d < r ＝ 2. 直线与圆的位置关系 设圆的半径为 r ，圆心到直线的距离为 d 直线与圆的位置关系 d 与 r 的关系 交点的个数 示意图 相离 d ＞ r 没有公共交点 直线与圆的位置关系 d 与 r 的关系 交点的个数 示意图 相切 d ＝ r 有且只有 ② ______ 公共点 相交 ③ ______ 有两个公共点 一个 d ＜ r 1 ．已知⊙ O 的半径是 4 ， OP ＝ 3 ，则点 P 与⊙ O 的位置关系是 ( 　　 ) A ．点 P 在圆内 B ．点 P 在圆上 C ．点 P 在圆外 D ．不能确定 2 ．已知⊙ O 的半径为 3 ，圆心 O 到直线 L 的距离为 2 ，则直线 L 与⊙ O 的位置关系是 ( 　　 ) A ．相交 B ．相切 C ．相离 D ．不能确定 练 提 分 必 A A 基础点 2 切线的性质与判定 1. 定义 ：直线和圆有 ④ ______ 公共点时，这条直线叫做圆的切线． 2. 性质 ：圆的切线垂直于过 ⑤ ______ 的半径． 3. 判定方法 (1) 已知切点：连接圆心和切点的半径，证明半径与要证的切线垂直，即“连半径，证垂直”． 一个 切点 (2) 未知切点：过圆心作出要证切线的垂线段，证明垂线 段的长等于半径，即“作垂线，证相等”． 4 ． 切线长 ：经过圆外一点作圆的切线，这点和 ⑥ _____ 之间线段的长，叫做这点到圆的切线长． 切点 5 ． 切线长定理 从圆外一点可以引圆的 ⑦ _____ 条切线，它们的切线长 ⑧ ______ ，这一点和圆心的连线平分两条切线的夹角．如图， PA 、 PB 切⊙ O 于 A 、 B 两点，则有 PA ＝ PB ，∠ APO ＝ ⑨ ______ ＝ ∠ APB . 相等 ∠ BPO 两 基础点 3 三角形的外接圆与内切圆 名称 三角形的外接圆 三角形的内切圆 圆心名称 三角形的外心 三角形的内心 描述 经过三角形的三个顶点的圆，外心是三角形三条边垂直平分线的交点 与三角形各边都相切的圆，内心是三角形三条角平分线的交点 名称 三角形的外接圆 三角形的内切圆 图形 性质 三角形的外心到三角形三个顶点的距离相等 三角形的内心到三角形三边的距离相等 重难点精讲优练 例 　 (2017 麓山国际实验学校三模 ) 如图，已知 AB 为⊙ O 的直径，点 E 在⊙ O 上，∠ EAB 的平分线交⊙ O 于点 C ，过点 C 作 AE 的垂线，垂足为 D ，直线 DC 与 AB 的延长线交于点 P. (1) 判断直线 PC 与⊙ O 的位置关系，并说明理由； 例 　 (2017 麓山国际实验学校三模 ) 如图，已知 AB 为⊙ O 的直径，点 E 在 ⊙ O 上，∠ EAB 的平分线交 ⊙ O 于点 C ，过点 C 作 AE 的垂线，垂足为 D ， 直线 DC 与 AB 的延长线交于点 P. (1) 判断直线 PC 与 ⊙ O 的位置关系，并说明理由； 【思维教练】 连接 OC ，要证 PC 是 ⊙ O 的切线，已 AD ⊥ DP ，只要证明 OC//AD ，推出 ∠ OCP =∠ D =90 °，即可得证 解： (1) PC 是 ⊙ O 的切线． 理由：如解图，连接 OC . ∵ AC 平分∠ EAB ，∴∠ EAC ＝∠ CAB ， 又∵ OA ＝ OC ，∴∠ CAB ＝∠ ACO ， ∴∠ EAC ＝∠ OCA ，∴ OC ∥ AD . ∵ AD ⊥ PD ，∴ OC ⊥ PD ，又∵ OC 是 ⊙ O 的半径， ∴ PC 是 ⊙ O 的切线； 例解图 (2) 若 tan ∠ P ＝ ， AD ＝ 6 ，求线段 AE 的长． 【 思维教练 】 由 OC ∥ AD ， 推出 ＝ ， 即 ＝ ， 连接 BE . 由 ∠ AEB ＝ 90° ， 推出 BE ∥ PD ，∠ ABE ＝ ∠ P ， AE ＝ AB · sin ∠ ABE ＝ AB · sin ∠ P ， 由此计算即可． 解： (2) 如解图，连接 BE . 在 Rt △ ADP 中，∠ ADP ＝ 90° ， AD ＝ 6 ， tan ∠ P ＝ ， ∴ PD ＝ 8 ， AP ＝ 10. 设半径为 r ，则 OP ＝ AP － AO ＝ 10 － r ， ∵ OC ∥ AD ， ∴ ＝ ，即 ＝ ， 解得 r ＝ . ∵ AB 是直径， ∴∠ AEB ＝∠ D ＝ 90° ，∴ BE ∥ PD ， ∴∠ ABE ＝∠ P ， ∴在 Rt △ ABE 中， AE ＝ AB · sin ∠ ABE ＝ AB · sin ∠ P ＝ ×2× ＝ . 练习 1 　如图，已知 AB 是 ⊙ O 的直径，点 C 在 ⊙ O 上，过点 C 的切线与 AB 的延长线交于点 P ，连接 AC . 若 ∠ A ＝ 30 ° ， PC ＝ 3 ，则 BP 的长为 ________ ． 练习 1 题图 【 解析 】 如解图，连接 OC ，∵ OA ＝ OC ，∠ A ＝ 30° ，∴∠ OCA ＝∠ A ＝ 30° ，∴∠ COB ＝∠ A ＋∠ ACO ＝ 60°.∵ PC 是⊙ O 的切线，∴∠ PCO ＝ 90° ，∠ P ＝ 30°.∵ PC ＝ 3 ，∴ OC ＝ PC · tan 30° ＝ 3× ＝ ， PO ＝ 2 OC ＝ 2 ，∴ PB ＝ PO － OB ＝ . 练习 1 解图 练习 2 　 (2017 株洲 ) 如图，已知 AM 是 ⊙ O 的直径，直线 BC 经过点 M ，且 AB ＝ AC ， ∠ BAM ＝ ∠ CAM ，线段 AB 和 AC 分别交 ⊙ O 于点 D 、 E ， ∠ BMD ＝ 40 ° ，则 ∠ EOM ＝ ________ 度． 练习 2 题图 【 解析 】 ∵ AB ＝ AC ，∠ BAM ＝∠ CAM ，∴ AM ⊥ BC ， ∴∠ AMD ＋∠ BMD ＝ 90° ，∴∠ AMD ＝ 50°. ∵ AM 是直径，∴∠ ADM ＝ 90° ，∠ AMD ＋∠ DAM ＝ 90° ， ∴∠ DAM ＝ 40° ，∴∠ MAE ＝ 40° ， ∴∠ EOM ＝ 2∠ MAE ＝ 80°. 练习 3 　如图， AB 是 ⊙ O 的直径，点 C 在 ⊙ O 上， AD 和过 C 点的切线互相垂直，垂足为 D . (1) 求证： AC 平分 ∠ DAB ； (2) 若点 M 是的中点， CM 交 AB 于点 N ， ⊙ O 的半径为 R ，求 MN · MC 的值． 练习 3 题图 【 解析 】 (1)证明：如解图，连接 OC ， ∵ CD 是 ⊙ O 的切线 ，∴ OC ⊥ CD . 又 ∵ AD ⊥ CD ，∴ OC ∥ AD ， ∴∠ OCA ＝ ∠ DAC. ∵ OA ＝ OC ， ∴∠ OAC ＝ ∠ OCA ， ∴∠ DAC ＝ ∠ OAC ，即 AC 平分 ∠ DAB ； 练习 3 解图 (2) 解： 如解图，连接 MA ， ∵点 M 是的中点， ∴ MA ＝ MB ，∠ MAB ＝∠ MBA ， 又∵∠ MBA ＝∠ MCA ， ∴∠ MAN ＝∠ MCA ， 又∵∠ NMA ＝∠ AMC ， ∴△ NMA ∽△ AMC ， 练习 3 解图 ∴ ＝ ， ∴ MN·MC ＝ MA 2 . ∵ AB 是⊙ O 的直径， MA ＝ MB, ∴△ MAB 是等腰直角三角形， ∴ MA 2 ＋ MB 2 ＝ AB 2 ＝ (2 R ) 2 ，即 2 MA 2 ＝ 4 R 2 ， ∴ MN·MC ＝ MA 2 ＝ 2 R 2 . 练习 3 解图