初中数学中考总复习课件PPT：第23课时　矩形、菱形、正方形 53页

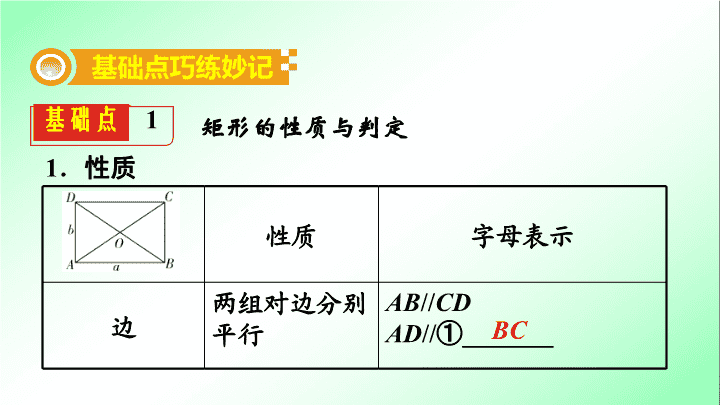
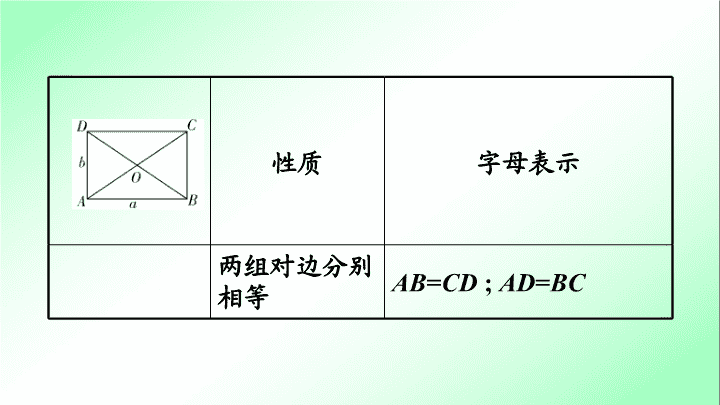
第一部分 夯实基础　提分多 第 五 单元 四边形 第 23 课时　矩形、菱形、正方形 1 ． 性质 基础点 1 矩形的性质与判定 性质 字母表示 边 两组对边分别平行 AB // CD AD // ① _______ BC 基础点巧练妙记 性质 字母表示 两组对边分别相等 AB = CD ; AD = BC 性质 字母表示 角 四个角都是直角 ∠ ABC = ∠ BCD= ∠ ABC = ∠ BCD=90° 对角线 对角线② __________ AC = BD ; OA = OB=OC = OD 互相平分且相等 性质 字母表示 对称性 既是中心对称图形又是轴对称图形，有两条对称轴 面积 S= ③ ______ ab 2. 判定 (1) 有一个角是直角的平行四边形是矩形； (2) 有三个角都是直角的四边形是矩形； (3) 对角线相等的平行四边形是矩形．            练 提 分 必 1 ．下列关于矩形的说法，正确的是 ( 　　 ) A ．对角线相等的四边形是矩形 B ．对角线互相平分的四边形是矩形 C ．矩形的对角线互相垂直且平分 D ．矩形的对角线相等且互相平分 D            练 提 分 必 2 ．如图， AB∥CD ，∠ A ＝∠ B ＝ 90 ° ， AB ＝ 3cm ， BC ＝ 2cm ，则 AB 与 CD 之间的距离为 ________cm. 第 2 题图 2 1 ． 性质 基础点 2 菱形的性质与判定 性质 字母表示 边 四边形④ _______ AB = BC=CD=DA 对边平行 AB // CD ; AD // BC 相等 性质 字母表示 角 对角相等 ∠ DAB = ∠ BCD ; ∠ ABC = ∠ ADC 对角线 对角线互相垂直且⑤ ______ AC ⊥⑥ _____ ； AO = OC,DO = OB 对角线平分一组对角 AC 平分∠ DAB 与∠ BCD;BD 平分∠ ABC 与∠ ADC 平分 BD 性质 字母表示 对称性 既是中心对称图形又是轴对称图形，有两条对称轴 面积 S= ⑦ ______ （ m 、 n 分别表示两条对角线的长）   2. 判定 (1) 有一组邻边相等的平行四边形是菱形； (2) 四条边都相等的平行四边形是菱形； (3) 对角线互相垂直的平行四边形是菱形．            练 提 分 必 3 ．下列四边形中不一定为菱形的是 ( 　　 ) A. 对角线相等的平行四边形 B. 每条对角线平分一组对角的四边形 C. 对角线互相垂直的平行四边形 D. 用两个全等的等边三角形拼成的四边形 A            练 提 分 必 4 ．如图，在菱形 ABCD 中， AB ＝ 3 ，∠ ACB ＝ 60 ° ，则对角线 AC 的长为 ( 　　 ) A ． 12 　　　　 B ． 9 C ． 6 　　 　 　 D ． 3 第 4 题图 D            练 提 分 必 5 ．如图，矩形 ABCD 的对角线 AC ， BD 相交于点 O ， CE ∥ BD ， DE ∥ AC ，若 AC ＝ 4 ，则四边形 CODE 的周长是 ________ ． 第 5 题图 8            练 提 分 必 6 ．一个平行四边形的一条边长为 5 ，两条对角线的长分别为 6 和 8 ，则它的面积为 ________ ． 24 1 ． 性质 基础点 3 正方形的性质与判定 性质 字母表示 边 四边形都⑧ _____ AB = BC=CD=AD 对边平行 AB // CD ; AD // BC 相等 性质 字母表示 角 四个角都是直角 ∠ ABC = ∠ ADC= ∠ BCD = ∠ BAD=90° 对角线 互相⑨ _______ 且相等 AC ⊥ BD , OA = OB=OC = OD 平分一组对角 AC 平分∠ DAB 与∠ BCD;BD 平分∠ ABC 与∠ ADC 垂直平分 性质 字母表示 对称性 既是中心对称图形又是轴对称图形，有 4 条对称轴 面积 S=a² （ a 表示正方形边长） 2. 判定 (1) 有一个角是直角的菱形是正方形； (2) 有一组邻边相等的矩形是正方形； (3) 对角线相等且互相垂直平分的平行四边形是正方形； (4) 四条边都相等且四个角都是直角的四边形是正方形．            练 提 分 必 7 ．如图，正方形 ABCD 的边长为 8 ，在各边上依次截取 AE ＝ BF ＝ CG ＝ DH ＝ 5 ，则四边形 EFGH 的面积是 ( 　　 ) A ． 30 　　　　　 B ． 34 C ． 36 　　　　　 D ． 40 第 7 题图 B 基础点 4 特殊四边形的关系 ( 掌握 ) 直角 相等 相等 直角 基础点 5 命题 命题： 判断一件事情的语句，叫做命题．命题分为题设和结论两部分． 真命题 ： 如果题设成立，那么结论一定成立，这样的命题叫做真命题． 假命题： 如果题设成立时，不能保证结论一定成立，这样的命题叫做假命题． 互逆命题 ： 在两个命题中，如果第一个命题的题设是另一个命题的结论，而第一个命题的结论是另一个命题的题设，那么这两个命题叫做互逆命题． 例 1 　如图，在▱ ABCD 中，∠ BAD 的平分线交 CD 于点 E ，交 BC 的延长线于点 F ，连接 BE ，∠ F ＝ 45 ° . (1) 求证：四边形 ABCD 是矩形； 重难点精讲优练 类型 1 矩形的相关证明与计算 例 1 题图 【 思维教练 】 要证四边形 ABCD 是矩形，根据已知条件▱ ABCD 的性质推出∠ F ＝∠ DAE ，由 AF 是∠ BAD 的平分线易得∠ DAB ＝ 90° ，结合矩形的判定方法，从而得证； 例 1 题图 证明 ：∵四边形 ABCD 是平行四边形， ∴ AD ∥ BC ，∴∠ DAE ＝∠ F ， ∵∠ F ＝ 45° ，∴∠ DAE ＝ 45° ， ∵ AF 是∠ BAD 的平分线， ∴∠ EAB ＝∠ DAE ＝ 45° ，∴∠ DAB ＝ 90° ，又∵四边形 ABCD 是平行四边形， ∴四边形 ABCD 是矩形； 例 1 题图   (2) 若 AB ＝ 14 ， DE ＝ 8 ，求 sin∠ AEB 的值． 例 1 题图 解 ：如解图，过点 B 作 BH ⊥ AE 于点 H ， ∵四边形 ABCD 是矩形， ∴ AB ＝ CD ， AD ＝ BC ，∠ DCB ＝∠ D ＝ 90° ， ∵ AB ＝ 14 ， DE ＝ 8 ，∴ CE ＝ 6 ， 在 Rt△ ADE 中，∠ DAE ＝ 45° ， ∴∠ DEA ＝∠ DAE ＝ 45° ， ∴ AD ＝ DE ＝ 8 ，∴ BC ＝ 8 ， 例 1 题解图   例 1 题解图 练习 1 　 (2017 咸宁 ) 如图，点 O 是矩形纸片 ABCD 的对称中心， E 是 BC 上一点，将纸片沿 AE 折叠后，点 B 恰好与点 O 重合，若 BE ＝ 3 ，则折痕 AE 的长为 ________ ． 练习 1 题图 6 【 解析 】 由折叠可知，∠ BAE ＝∠ OAE ，∠ EOA ＝∠ B ＝ 90° ，∵ O 是矩形 ABCD 的对称中心，∴ OA ＝ OC ，∴ EO 是 AC 的垂直平分线，易证∠ ECO ＝∠ EAO ，在三角形 ABC 中，可利用三角形内角和为 180° ，求得∠ BAE ＝ 30° ， 练习 1 题图 在直角三角形 ABE 中，∠ B ＝ 90° ，∠ BAE ＝ 30° ，由 30° 所对的直角边是斜边的一半，可得到 AE ＝ 6.            导 方 法 指 1 ．矩形判定的一般思路： （ 1 ）一个内角为 90° （ 2 ）对角线相等 四边形 + 有三个内角是直角 平行四边形 +            练 提 分 必 2 ．应用矩形性质计算的一般思路： (1) 根据矩形的四个角都是直角，一条对角线将矩形分成两个直角三角形，可用勾股定理或解直角三角形求线段的长； (2) 又根据矩形对角形相等且互相平分，故可借助对角线的关系得到全等三角形；            练 提 分 必 (3) 矩形的两条对角线把矩形分成四个等腰三角形，在矩形性质相关的计算和证明中要注意这个结论的运用，建立能够得到线段或角度的等量关系． 类型 2 菱形的相关证明与计算 例 2 　 如图，在平行四边形 ABCD 中，边 AB 的垂直平分线交 AD 于点 E ，交 CB 的延长线于点 F ，连接 AF ， BE . (1) 求证：△ AGE ≌△ BGF ； 【 思维教练 】 要证△ AGE ≌△ BGF ，根据平行四边形 ABCD 的性质，结合全等三角形的判定方法 AAS 即可求证； 例 2 题图 证明： 在平行四边形 ABCD 中， AD ∥ CF ， ∴∠ AEG ＝∠ BFG ， ∵ AB 的垂直平分线交 AD 于点 E ， ∴ AG ＝ BG ， 又∵∠ AGE ＝∠ BGF ， ∴△ AGE ≌△ BGF ( AAS ) ； 例 2 题图 (2) 试判断四边形 AFBE 的形状，并说明理由． 【 思维教练 】 要判断四边形 AFBE 的形状，由 (1) 易得 AE ＝ BF ， AE ∥ BF ，可推出四边形 AFBE 为平行四边形，结合 EF 垂直平分 AB 推出 AE ＝ BE ，从而得证． 例 2 题图 解： 四边形 AFBE 为菱形． 理由：由 (1) 得 AE ＝ BF ， AE ∥ BF , 则四边形 AFBE 为平行四边形， 又∵ EF 垂直平分 AB ， ∴ AE ＝ BE ， ∴四边形 AFBE 为菱形． 例 2 题图 练习 2 　 (2017 孝感 ) 如图，四边形 ABCD 是菱形， AC ＝ 24 ， BD ＝ 10 ， DH ⊥ AB 于点 H ，则线段 BH 的长为 ________ ． 练习 2 题图              导 方 法 指 菱形判定的一般思路： (1) 一组邻边相等 (2) 对角线互相垂直 四边形 + 四边相等 平行四边形 + 菱形            导 方 法 指 2 ．菱形的计算： (1) 求角度时，应注意菱形的四条边相等和对角相等、邻角互补等，可利用等腰三角形的性质和平行线的相交性质，转化要求的角，直到找到与已知的角存在的关系；            导 方 法 指 (2) 求长度 ( 线段或者周长 ) 时，应注意使用等腰三角形的性质．若菱形中有一个角为 60° ，则连接另外两点的对角线所分割的两个三角形为等边三角形，故在计算时，可借助等边三角形的性质求线段长； (3) 求面积时，可利用菱形的两条对角线互相垂直，面积等于对角线之积的一半求解． 类型 3 正方形的相关证明与计算 例 2 　 如图，四边形 ABCD 是正方形，△ EBC 是等边三角形． (1) 求证：△ ABE ≌△ DCE ； 【 思维教练 】 要证△ ABE ≌△ DCE ，根据正方形 ABCD 和等边△ EBC 的性质推出 AB ＝ CD ，∠ ABE ＝∠ DCE ，结合全等三角形的判定方法 SAS 即可求证； 例 2 题图 证明： ∵四边形 ABCD 是正方形， ∴ AB ＝ CD ，∠ ABC ＝∠ DCB ＝ 90° ， ∵△ EBC 是等边三角形， ∴ EB ＝ EC ，∠ EBC ＝∠ ECB ＝ 60° ， ∴∠ ABC －∠ EBC ＝∠ DCB －∠ ECB ＝ 30° ，即∠ ABE ＝∠ DCE ＝ 30° ， 在△ ABE 和△ DCE 中， AB=BC ∠ ABE = ∠ DCE =30° EB = EC ∴△ ABE ≌ DCE (SAS). (2) 求∠ AED 的度数． 【 思维教练 】 由已知条件推出△ ABE 、△ CDE 、△ ADE 都是等腰三角形，求得∠ EAB ＝∠ CDE ＝ 75° ，根据三角形内角和即可求解∠ AED 的度数． 解： ∵四边形 ABCD 是正方形，△ EBC 是等边三角形， ∴△ ABE 、△ CDE 、△ ADE 都是等腰三角形， ∵∠ ABE ＝∠ DCE ＝ 30° ， ∴∠ EAB ＝ (180° － 30°)÷2 ＝ 75° ， 同理∠ CDE ＝ 75° ， ∴∠ EAD ＝∠ EDA ＝ 90° － 75° ＝ 15° ， ∴∠ AED ＝ 180° － 2×15° ＝ 150°.   练习 3 题图 A 练习 3 题解图   练习 3 题解图   练习 3 题解图