九年级数学下册第25章投影与视图25-1投影课时作业新版沪科版 11页

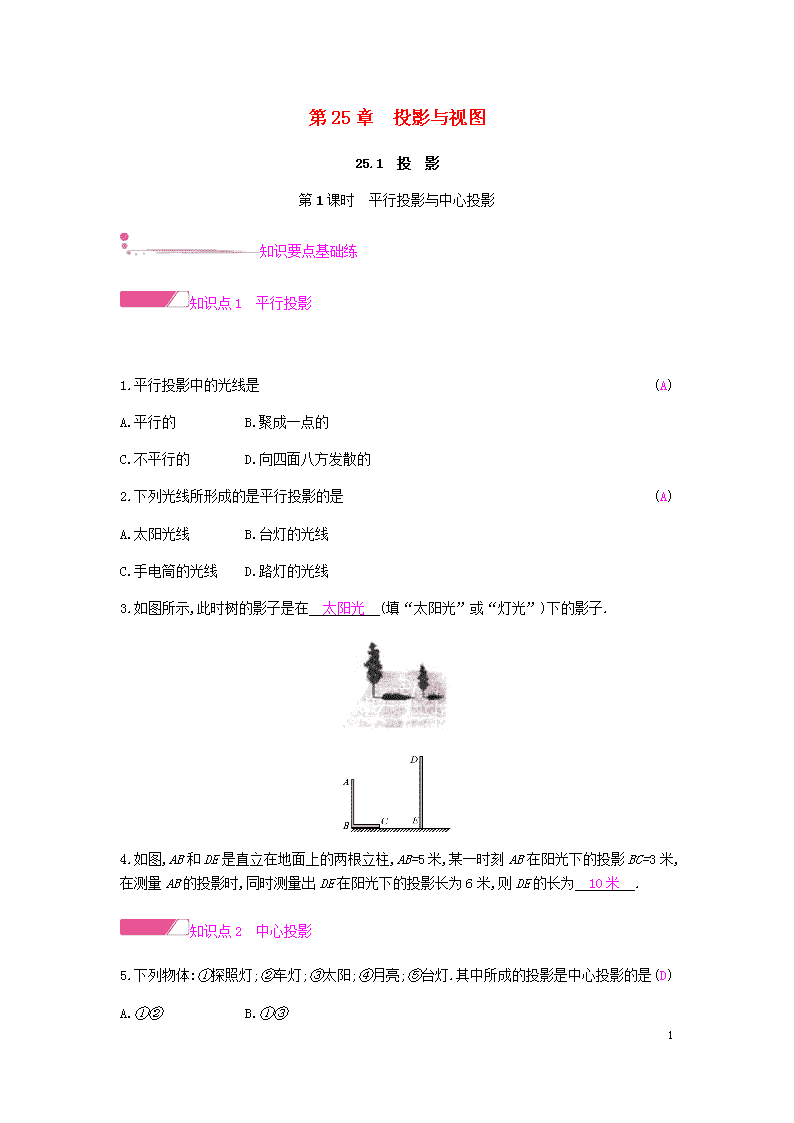
第25章　投影与视图 ‎25.1　投　影 第1课时　平行投影与中心投影 知识要点基础练 知识点1　平行投影 ‎1.平行投影中的光线是(A)‎ A.平行的 B.聚成一点的 C.不平行的 D.向四面八方发散的 ‎2.下列光线所形成的是平行投影的是(A)‎ A.太阳光线 B.台灯的光线 C.手电筒的光线 D.路灯的光线 ‎3.如图所示,此时树的影子是在　太阳光　(填“太阳光”或“灯光”)下的影子. ‎ ‎4.如图,AB和DE是直立在地面上的两根立柱,AB=5米,某一时刻AB在阳光下的投影BC=3米,在测量AB的投影时,同时测量出DE在阳光下的投影长为6米,则DE的长为　10米　. 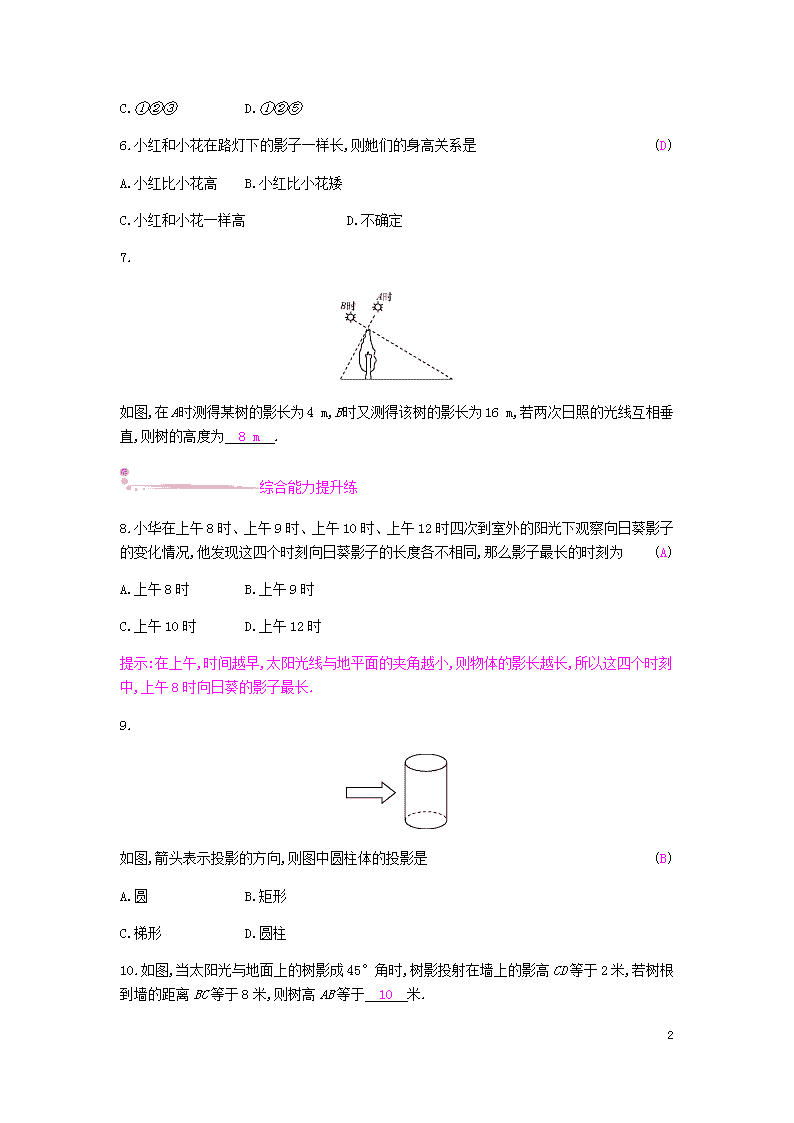‎ 知识点2　中心投影 ‎5.下列物体:①探照灯;②车灯;③太阳;④月亮;⑤台灯.其中所成的投影是中心投影的是(D)‎ A.①② B.①③‎ 11‎ C.①②③ D.①②⑤‎ ‎6.小红和小花在路灯下的影子一样长,则她们的身高关系是(D)‎ A.小红比小花高 B.小红比小花矮 C.小红和小花一样高 D.不确定 ‎7.‎ 如图,在A时测得某树的影长为4 m,B时又测得该树的影长为16 m,若两次日照的光线互相垂直,则树的高度为　8 m　. ‎ 综合能力提升练 ‎8.小华在上午8时、上午9时、上午10时、上午12时四次到室外的阳光下观察向日葵影子的变化情况,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为(A)‎ A.上午8时 B.上午9时 C.上午10时 D.上午12时 提示:在上午,时间越早,太阳光线与地平面的夹角越小,则物体的影长越长,所以这四个时刻中,上午8时向日葵的影子最长.‎ ‎9.‎ 如图,箭头表示投影的方向,则图中圆柱体的投影是(B)‎ A.圆 B.矩形 C.梯形 D.圆柱 ‎10.如图,当太阳光与地面上的树影成45°角时,树影投射在墙上的影高CD等于2米,若树根到墙的距离BC等于8米,则树高AB等于　10　米. 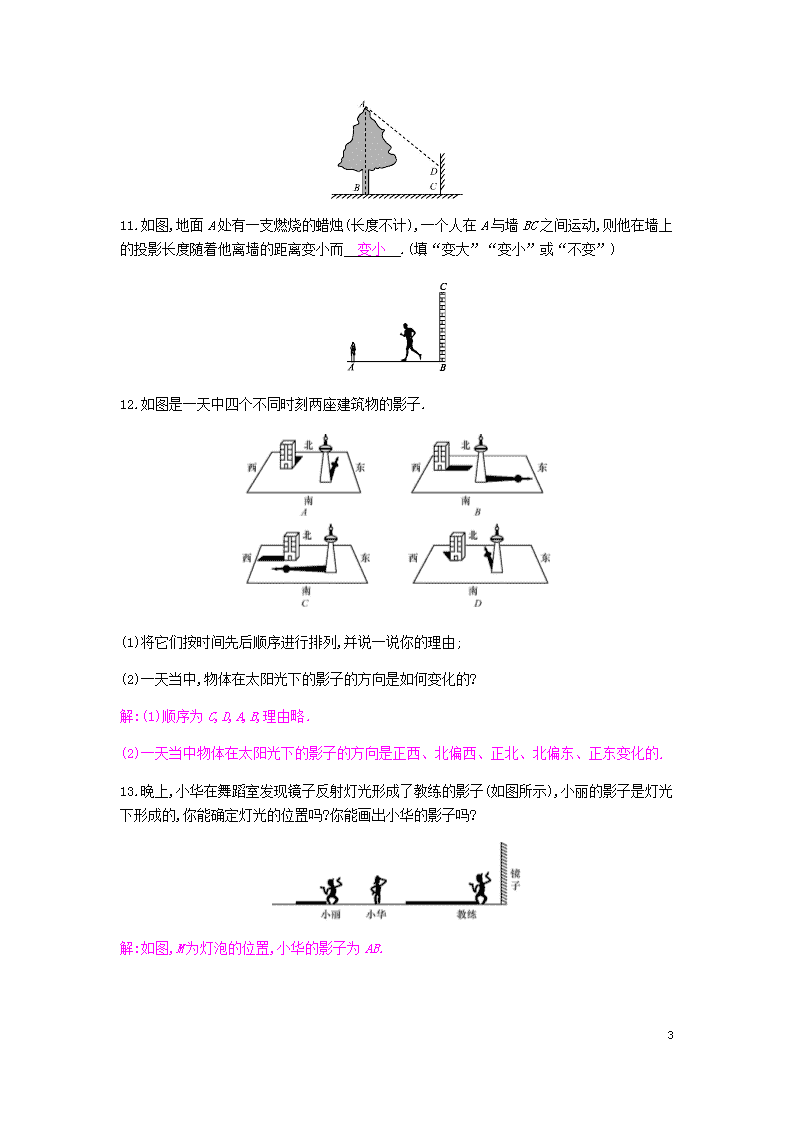‎ 11‎ ‎11.如图,地面A处有一支燃烧的蜡烛(长度不计),一个人在A与墙BC之间运动,则他在墙上的投影长度随着他离墙的距离变小而　变小　.(填“变大”“变小”或“不变”) ‎ ‎12.如图是一天中四个不同时刻两座建筑物的影子.‎ ‎(1)将它们按时间先后顺序进行排列,并说一说你的理由;‎ ‎(2)一天当中,物体在太阳光下的影子的方向是如何变化的?‎ 解:(1)顺序为C,D,A,B,理由略.‎ ‎(2)一天当中物体在太阳光下的影子的方向是正西、北偏西、正北、北偏东、正东变化的.‎ ‎13.晚上,小华在舞蹈室发现镜子反射灯光形成了教练的影子(如图所示),小丽的影子是灯光下形成的,你能确定灯光的位置吗?你能画出小华的影子吗?‎ 解:如图,M为灯泡的位置,小华的影子为AB.‎ 11‎ ‎14.如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,求树高AB.(结果保留根号)‎ 解:在Rt△ABD中,∵tan∠ADB=ABBD,‎ ‎∴BD=ABtan60°‎‎=‎AB‎3‎,‎ 在Rt△ACB中,∵tan∠ACB=ABBC,‎ ‎∴BC=ABtan30°‎‎=AB‎3‎‎3‎=‎‎3‎AB,‎ ‎∵BC-BD=8,∴‎3‎AB-AB‎3‎=8,∴AB=4‎3‎.‎ 答:树高AB为4‎3‎ 米.‎ ‎15.如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.‎ ‎(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.‎ ‎(2)如果小明的身高AB=1.6 m,他的影子长AC=1.4 m,且他到路灯的距离AD=2.1 m,求灯泡的高.‎ 解:(1)如图,点O为灯泡所在的位置,‎ 11‎ 线段FH为小亮在灯光下形成的影子.‎ ‎(2)根据题意,得ABOD‎=‎CACD,∴‎1.6‎OD‎=‎‎1.4‎‎1.4+2.1‎,‎ ‎∴OD=4 m.‎ 答:灯泡的高为4 m.‎ 拓展探究突破练 ‎16.为了利用太阳光线或其他方法测量一棵大树的高度,准备了如下测量工具:①镜子;②皮尺;③长为2 m的标杆;④高为1.5 m的测角仪.请你根据你所设计的测量方案,回答下列问题:‎ ‎(1)在你的设计方案中,选用的测量工具是　　　　;(填写工具序号) ‎ ‎(2)在图中画出你的方案示意图;‎ ‎(3)你需要测量示意图中哪些数据,并用a,b,c表示测得的数据;‎ ‎(4)写出求树高AB的算式.‎ 解:答案不唯一,合理即可.‎ 方案一:‎ ‎(1)①②.‎ ‎(2)测量方案示意图如图1.‎ ‎(3)CA=a,CD=b,DE(眼睛到地面的高度)=c.‎ ‎(4)AB=acb.‎ 11‎ 方案二:‎ ‎(1)②③.‎ ‎(2)测量方案示意图如图2(其中BC为太阳光线).‎ ‎(3)AC=a,CD=b,ED=c=2 m.‎ ‎(4)AB=‎2ab.‎ 第2课时　正投影 知识要点基础练 知识点1　正投影的概念 ‎1.如图所示,水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影图是(D)‎ ‎2.在平行投影中,如果投影线　垂直　于投影面,那么这种投影称为正投影. ‎ ‎3.下列投影是正投影的是　③④　.(填序号) ‎ 11‎ 知识点2　正投影的性质 ‎4.一支铅笔 (记为线段AB),它的正投影为线段CD,则下列各式中一定成立的是(D)‎ A.AB=CD B.AB≤CD C.AB>CD D.AB≥CD ‎5.一块圆形铁片,它的正投影是(D)‎ A.圆 B.椭圆 C.线段 D.不能确定 ‎【变式拓展】正方形在太阳光的投影下得到的几何图形一定是(B)‎ A.正方形 B.平行四边形或一条线段 C.矩形 D.菱形 ‎6.(绥化中考)正方形的正投影不可能是(D)‎ A.线段 B.矩形 C.正方形 D.梯形 ‎7.平行于投影面的平行四边形的面积　等于　它的正投影的面积.(填“大于”“小于”或“等于”) ‎ 综合能力提升练 ‎8.如图所示的圆台的上下底面与投影线平行,圆台的正投影是(C)‎ 11‎ A.矩形 B.两条线段 C.等腰梯形 D.圆环 ‎9.下列说法正确的是(B)‎ A.正投影是中心投影的一种特例 B.正投影是平行投影的一种特例 C.正投影既不是平行投影也不是中心投影 D.平行投影就是正投影 ‎10.一个圆柱形的茶叶盒在太阳光下旋转,其影子的变化过程可能是(D)‎ A.矩形、矩形、圆 B.正方形、圆、矩形 C.圆、矩形、矩形 D.无法确定 ‎11.如图所示是一个圆锥在某平面上的正投影,则该圆锥的侧面积是 ‎15‎‎4‎π　. ‎ ‎12.如图所示,地面上直立一根标杆AB,杆长为2 m.‎ ‎(1)当阳光垂直照射地面时,标杆在地面上的投影是什么图形?‎ ‎(2)当阳光与地面的倾斜角为60°时,标杆在地面上的投影是什么图形?并画出投影示意图.‎ 答案图 11‎ 解:(1)阳光垂直地面时,产生的投影是正投影,是一个与标杆的正切面相等的圆.‎ ‎(2)如图所示,标杆在地面上的投影为BC.在Rt△ABC中,BC=ABtan60°‎‎=‎2‎‎3‎=‎‎2‎‎3‎‎3‎,所以标杆在地面上的投影是长度为‎2‎‎3‎‎3‎ m的线段.‎ ‎13.指出如图所示的几何体各个面的正投影图形,并画出投影线的方向如箭头所示时该几何体的正投影.‎ 解:立体图形除正面和后面的正投影为五边形外,其他的正投影为大小不同的矩形(图略).‎ ‎14.一个水平放在桌面上的圆柱,从前向后形成的正投影是一个边长为20 cm的正方形,求此圆柱的表面积.‎ 解:依题意,该圆柱的高为20 cm,底面直径为20 cm.‎ 则S=2·‎20‎‎2‎‎2‎·π+20π·20=600π cm2,‎ 所以此圆柱的表面积为600π cm2.‎ ‎15.如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.‎ 11‎ 解:延长OD,∵DO⊥BF,∴∠DOE=90°.‎ ‎∵OD=0.8 m,OE=0.8 m,‎ ‎∴∠DEB=45°.‎ ‎∵AB⊥BF,‎ ‎∴∠BAE=45°,∴AB=BE.‎ 设AB=BE=x m,∵AB⊥BF,CO⊥BF,‎ ‎∴AB∥CO,‎ ‎∴△ABF∽△COF,∴ABBF‎=‎COOF,‎ 即xx+(3-0.8)‎‎=‎‎1.2+0.8‎‎3‎,‎ 解得x=4.4.‎ 经检验:x=4.4是原方程的解.‎ 答:围墙AB的高度是4.4 m.‎ 拓展探究突破练 ‎16.一个圆柱的轴截面平行于投影面,圆柱的正投影是邻边长分别为4 cm,3 cm的矩形,求圆柱的表面积和体积.‎ 解:由题可知,有两种情况:①当圆柱底面圆的半径为1.5 cm,高为4 cm时,‎ 11‎ 圆柱的表面积为2π×‎3‎‎2‎×4+2π×‎3‎‎2‎‎2‎=12π+‎9‎‎2‎π=‎33‎‎2‎π cm2,‎ 体积为π‎3‎‎2‎‎2‎×4=9π cm3;‎ ‎②当圆柱底面圆的半径为2 cm,高为3 cm时,‎ 圆柱的表面积为2π×2×3+2π×22=12π+8π=20π cm2,‎ 体积为π×22×3=12π cm3.‎ 11‎