2017-2018学年安徽省合肥市初中毕业班 第3次十校联考 数学试题（Word版 附答案） 5页

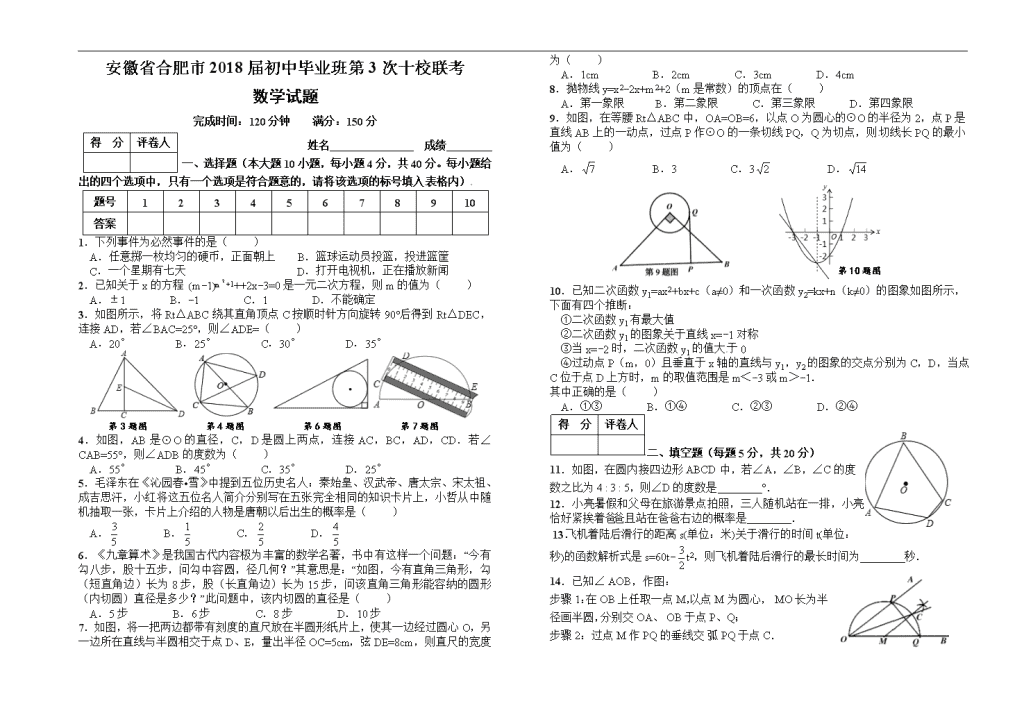
安徽省合肥市2018届初中毕业班第3次十校联考 数学试题 得 分 评卷人 完成时间：120分钟 满分：150分 姓名 成绩 ‎ 一、选择题（本大题10小题，每小题4分，共40分。每小题给出的四个选项中，只有一个选项是符合题意的，请将该选项的标号填入表格内） ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 ‎1．下列事件为必然事件的是（　 　） ‎ A．任意掷一枚均匀的硬币，正面朝上 B．篮球运动员投篮，投进篮筐[来源:学*科*网]‎ C．一个星期有七天 D．打开电视机，正在播放新闻 ‎2．已知关于x的方程 (m-1)m+1++2x-3=0是一元二次方程，则m的值为（　 　） ‎ A．±1 B．-1 C．1 D．不能确定 ‎3．如图所示，将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC，连接AD，若∠BAC=25°，则∠ADE=（　 　）‎ A．20° B．25° C．30° D．35°‎ ‎ ‎ ‎ 第3题图 第4题图 第6题图 第7题图 ‎4．如图，AB是⊙O的直径，C，D是圆上两点，连接AC，BC，AD，CD．若∠CAB=55°，则∠ADB的度数为（　 　）‎ A．55° B．45° C．35° D．25°‎ ‎5．毛泽东在《沁园春•雪》中提到五位历史名人：秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗，小红将这五位名人简介分别写在五张完全相同的知识卡片上，小哲从中随机抽取一张，卡片上介绍的人物是唐朝以后出生的概率是（　 　）‎ A． B． C． D．‎ ‎6．《九章算术》是我国古代内容极为丰富的数学名著，书中有这样一个问题：“今有勾八步，股十五步，问勾中容圆，径几何？”其意思是：“如图，今有直角三角形，勾（短直角边）长为8步，股（长直角边）长为15步，问该直角三角形能容纳的圆形（内切圆）直径是多少？”此问题中，该内切圆的直径是（　 　）‎ A．5步 B．6步 C．8步 D．10步 ‎7．如图，将一把两边都带有刻度的直尺放在半圆形纸片上，使其一边经过圆心O，另一边所在直线与半圆相交于点D、E，量出半径OC=5cm，弦DE=8cm，则直尺的宽度为（　 　）‎ A．1cm B．2cm C．3cm D．4cm ‎8．抛物线y=x2-2x+m2+2（m是常数）的顶点在（　 　） ‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎9．如图，在等腰Rt△ABC中，OA=OB=6，以点O为圆心的⊙O的半径为2，点P是直线AB上的一动点，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为（　 　） ‎ A． B．3 C．3 D．‎ 第10题图 ‎ ‎ ‎10．已知二次函数y1=ax2+bx+c（a≠0）和一次函数y2=kx+n（k≠0）的图象如图所示，下面有四个推断： ①二次函数y1有最大值 ②二次函数y1的图象关于直线x=-1对称 ③当x=-2时，二次函数y1的值大于0 ④过动点P（m，0）且垂直于x轴的直线与y1，y2的图象的交点分别为C，D，当点C位于点D上方时，m的取值范围是m＜-3或m＞-1． 其中正确的是（　 　）‎ A．①③ B．①④ C．②③ D．②④‎ 得 分 评卷人 二、填空题（每题5分，共20分）‎ ‎11．如图，在圆内接四边形ABCD中，若∠A，∠B，∠C的度数之比为4 : 3 : 5，则∠D的度数是 °．‎ ‎12．小亮暑假和父母在旅游景点拍照，三人随机站在一排，小亮恰好紧挨着爸爸且站在爸爸右边的概率是 ．‎ ‎ 13．飞机着陆后滑行的距离s(单位：米)关于滑行的时间t(单位：秒)的函数解析式是s=60t-t2，则飞机着陆后滑行的最长时间为 秒．‎ ‎14．已知∠ AOB，作图：  步骤1：在 OB上任取一点 M，以点 M为圆心， MO长为半径画半圆，分别交 OA、 OB于点 P、Q； 步骤2：过点 M作 PQ的垂线交 弧PQ于点 C．  ‎ 步骤3：画射线 OC．  则下列判断：① 弧PC=弧CQ；② MC∥ OA；③ OP＝PQ；④ OC平分∠AOB．其中正确的为（填序号） ．‎ 得 分 评卷人 三、（每小题8分，共16分）‎ ‎15．解方程：解方程：2x2-4x-1=0．‎ ‎[来源:学|科|网]‎ ‎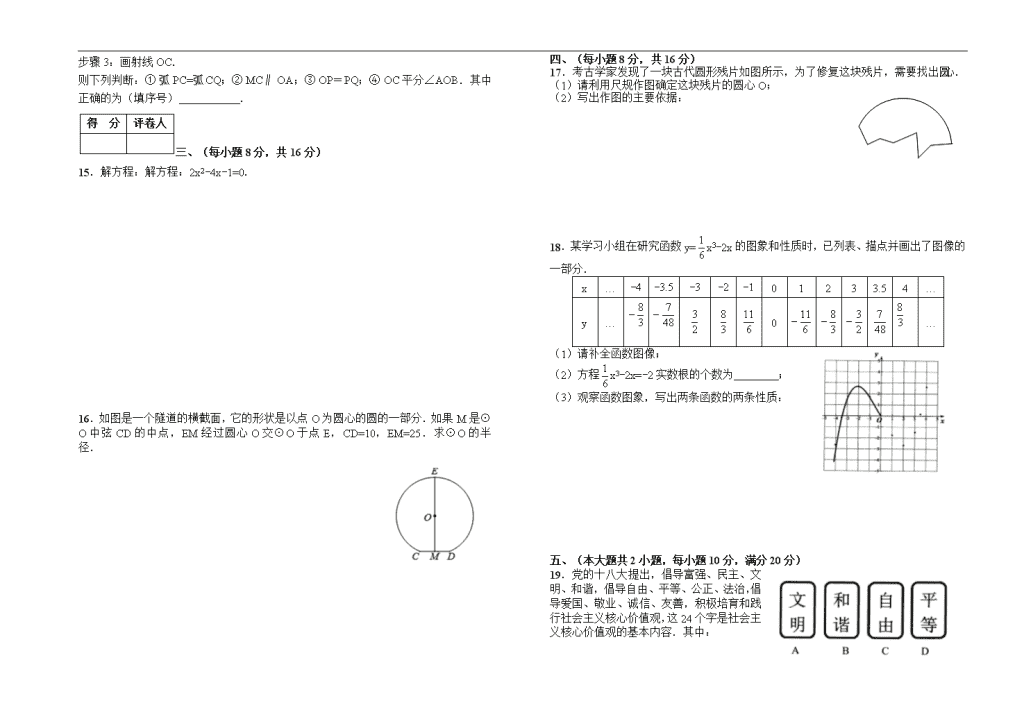16．如图是一个隧道的横截面，它的形状是以点O为圆心的圆的一部分．如果M是⊙O中弦CD的中点，EM经过圆心O交⊙O于点E，CD=10，EM=25．求⊙O的半径．‎ 四、（每小题8分，共16分）‎ ‎17．考古学家发现了一块古代圆形残片如图所示，为了修复这块残片，需要找出圆心． （1）请利用尺规作图确定这块残片的圆心O； （2）写出作图的主要依据：‎ ‎18．某学习小组在研究函数y=x3-2x的图象和性质时，已列表、描点并画出了图像的一部分．‎ x ‎…‎ ‎-4‎ ‎-3.5‎ ‎-3‎ ‎-2‎ ‎-1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎3.5‎ ‎4‎ ‎…‎ y ‎…‎ ‎0‎ ‎[来源:学科网]‎ ‎…‎ ‎（1）请补全函数图像；‎ ‎（2）方程x3-2x=-2实数根的个数为 ； （3）观察函数图象，写出两条函数的两条性质：‎ 五、（本大题共2小题，每小题10分，满分20分）‎ ‎19．党的十八大提出，倡导富强、民主、文明、和谐，倡导自由、平等、公正、法治，倡导爱国、敬业、诚信、友善，积极培育和践行社会主义核心价值观，这24个字是社会主义核心价值观的基本内容．其中： ‎ ‎ “富强、民主、文明、和谐”是国家层面的价值目标； “自由、平等、公正、法治”是社会层面的价值取向； “爱国、敬业、诚信、友善”是公民个人层面的价值准则． 小光同学将其中的“文明”、“和谐”、“自由”、“平等”的文字分别贴在4张硬纸板上，制成如图所示的卡片．将这4张卡片背面朝上洗匀后放在桌子上，从中随机抽取一张卡片，不放回，再随机抽取一张卡片． （1）小光第一次抽取的卡片上的文字是国家层面价值目标的概率是 ； （2）请你用列表法或画树状图法，帮助小光求出两次抽取卡片上的文字一次是国家层面价值目标、一次是社会层面价值取向的概率（卡片名称可用字母表示）．‎ ‎20．如图，等边三角形ABC内接于半径为1的⊙O，以BC为一边作⊙O的内接矩形BCDE，则矩形BCDE的面积．‎ ‎[来源:学科网]‎ 六、（本大题满分12分）‎ ‎21．如图，在边长为1的正方形组成的网格中建立直角坐标系，△AOB的顶点均在格点上，点O为原点，点A、B的坐标分别是A（3，2）、B（1，3）． （1）画出△AOB向下平移3个单位后得到的△A1O1B1，则点B1的坐标为 ； （2）将△AOB绕点O逆时针旋转90°后得到△A2OB2，请在图中作出△A2OB2，这时点A2的坐标为 ； （3）在（2）中的旋转过程中，求线段OA扫过的图形的面积．‎ 七、（本大题满分12分）‎ ‎22．如图，在直角梯形ABCD中，AB∥CD，∠B=90。，AB=AD，∠BAD的平分线交BC于E，连接DE．‎ ‎（1）说明点D在△ABE的外接圆上；‎ ‎（2）若∠AED=∠CED，试判断直线CD与△ABE外接圆的位置关系，并说明理由．‎ 八、（本大题满分14分）‎ ‎23．如图所示，在平面直角坐标系中，A、B为x轴上两点，C、D为y轴上两点，经过点A，C，B的抛物线的一部分C1与经过点A，D，B的抛物线的一部分C2组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”． 已知点C的坐标为（0，-），点M是抛物线C2：y=mx2-2mx-3m（m＜0）的顶点 （1）求A、B两点的坐标； （2）求经过点A，C，B的抛物线C1的函数表达式． （3）探究“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出点P的坐标及△PBC面积的最大值；若不存在，请说明理由．‎ 安徽省合肥市2018届初中毕业班第3次十校联考 数学试题 参考答案 一、选择题（本大题10小题，每小题4分，共40分） ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 C B A C C B C A D D 二、填空题（每题5分，共20分）‎ ‎11．120． 12． ．  13．20． 14．①②④．‎ 三、（每小题8分，共16分）‎ ‎15．解：原方程化为x2-2x=， 配方得x2-2x+1=+1， 即 (x-1)2=， 开方得x-1=±， x=1±，‎ ‎∴ x1=1+，x2=1-．‎ ‎16．解：如图，连接OC， ∵M是弦CD的中点，EM过圆心O， ∴EM⊥CD． ∴CM=MD． ∵CD=10， ∴CM=5． 设OC=x，则OM=25-x， 在Rt△COM中，根据勾股定理，得 52+(25-x) 2=x2． 解得 x=13． ∴⊙O的半径为13．‎ 四、（每小题8分，共16分）‎ ‎17．（1）如图所示，点O即为所求作的圆心； （2）作图的依据： 线段垂直平分线上的点与线段两个端点的距离相等；不在同一直线上的三个点确定一个圆．‎ ‎18．（1）函数图像如图；（2）3； （3）函数的性质：‎ ‎1．此函数在实数范围内既没有最大值，也没有最小值，‎ ‎2．此函数在x＜-2和x＞2时，y随x的增大而增大，‎ ‎3．此函数在-2＜x＜2时，y随x的增大而减小，[来源:Z#xx#k.Com]‎ ‎4．此函数图象过原点，‎ ‎5．此函数图象关于原点对称．‎ 五、（本大题共2小题，每小题10分，满分20分）‎ ‎19．（1）；（2）画树状图为： ‎ ‎ 共有12种等可能的结果数，其中两次抽取卡片上的文字一次是国家层面价值目标、一次是社会层面价值取向的结果数为8， 所以两次抽取卡片上的文字一次是国家层面价值目标、一次是社会层面价值取向的概率==．‎ ‎20．解：连接BD，如图所示： ∵△ABC是等边三角形， ∴∠BAC=60°， ∴∠BDC=∠BAC=60°， ∵四边形BCDE是矩形， ∴∠BCD=90°， ∴BD是⊙O的直径，∠CBD=90°-60°=30°， ∴BD=2，CD=BD=1， ∴BC==， ∴矩形BCDE的面积=BC•CD=×1=；‎ 六、（本大题满分12分）‎ ‎21．（1）（1，0）；（2）（-2，3）； 作图如图所示： （3）由勾股定理，得OA=， ∴线段OA扫过的图形的面积为：=π．‎ 七、（本大题满分12分）‎ ‎22．（1）证明：∵∠B=90°， ∴AE是△ABE外接圆的直径．           取AE的中点O，则O为圆心，连接OB、OD．          ∵AB=AD，∠BAO=∠DAO，AO=AO， ‎ ‎          ∴△AOB≌△AOD． ∴OD=OB．             ∴点D在△ABE的外接圆上； （2）证明：直线CD与△ABE的外接圆相切．       理由：∵AB∥CD， ∠B=90°． ∴∠C=90°．                   ∴∠CED+∠CDE=90°．             又∵OE=OD， ∴∠ODE=∠OED． 又∠AED=∠CED，            ∴∠ODE=∠DEC． ∴∠CDE+∠ODE=∠CDE+∠CED=90°．              ∴CD与△ABE的外接圆相切．‎ 八、（本大题满分14分）‎ ‎23．（1）∵y=mx2-2mx-3m=m(x-3)(x+1)，且m≠0， ∴当y=0时，可得m(x-3)(x+1)=0，解得x1=-1，x2=3， ∴A（-1，0），B（3，0）；‎ a=‎ 解得 b=−1‎ c=−‎ ‎（2）设过A、B、C三点的抛物线解析式为y=ax2+bx+c， 则有 a−b+c=0‎ ‎9a+3b+c=0‎ c=−，‎ ‎∴抛物线C1解析式为y=x2−x−； （3）如图，过点P作PQ∥y轴，交BC于Q， 设直线BC解析式为y=kx+s，则有 解得 k=‎ s=-‎ ‎3k+s=0‎ s=−， ∴直线BC的解析式为y=x-， 设P（x，x2-x-），则Q（x，x-）， ∴PQ=x--(x2-x-)=x2+x， ∴S△PBC=PQ•OB=×(x2+x)×3=(x)2+， ∵＜0， ∴当x=时，S△PBC有最大值，S最大=，此时P点纵坐标为×（）2=-， 此时P点坐标为（，-）．‎