- 265.00 KB
- 2021-11-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
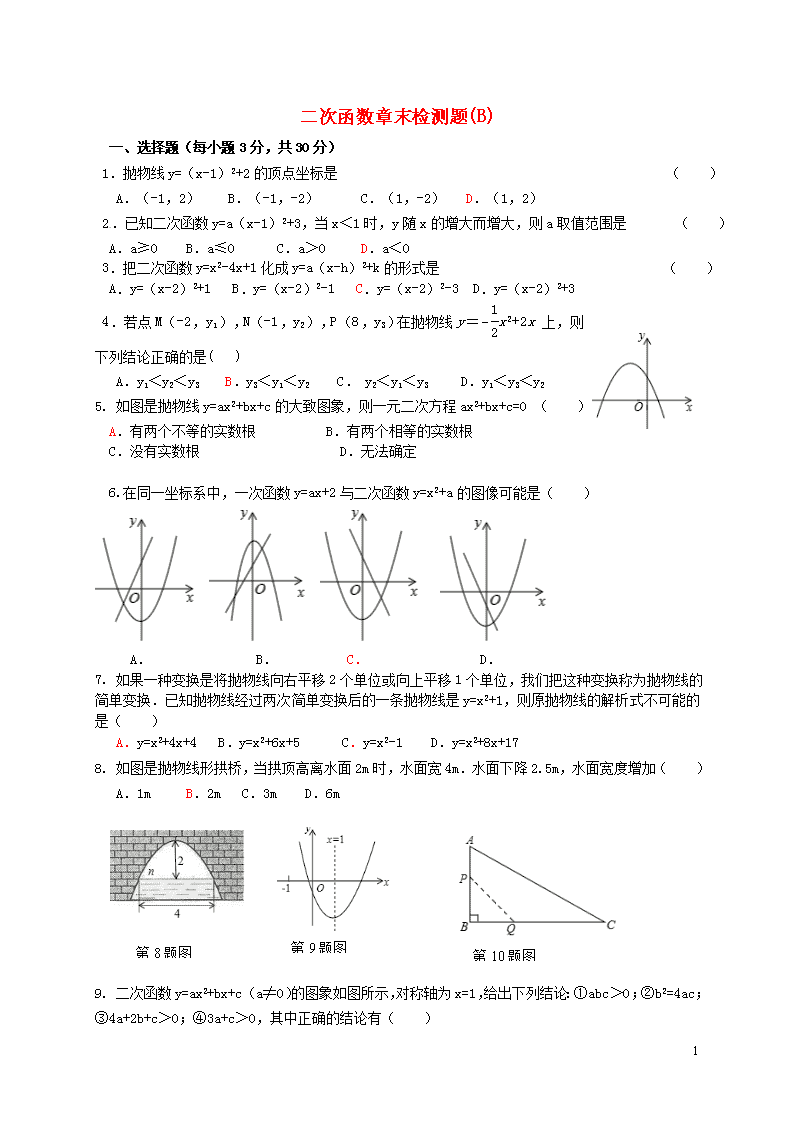
二次函数章末检测题(B)
一、选择题(每小题3分,共30分)
1.抛物线y=(x-1)2+2的顶点坐标是 ( )
A.(-1,2) B.(-1,-2) C.(1,-2) D.(1,2)
2.已知二次函数y=a(x-1)2+3,当x<1时,y随x的增大而增大,则a取值范围是 ( )
A.a≥0 B.a≤0 C.a>0 D.a<0
3.把二次函数y=x2-4x+1化成y=a(x-h)2+k的形式是 ( )
A.y=(x-2)2+1 B.y=(x-2)2-1 C.y=(x-2)2-3 D.y=(x-2)2+3
4.若点M(-2,y1),N(-1,y2),P(8,y3)在抛物线y=−x2+2x上,则下列结论正确的是( )
A.y1<y2<y3 B.y3<y1<y2 C. y2<y1<y3 D.y1<y3<y2
5. 如图是抛物线y=ax2+bx+c的大致图象,则一元二次方程ax2+bx+c=0 ( )
A.有两个不等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
6.在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图像可能是( )
A. B. C. D.
7. 如果一种变换是将抛物线向右平移2个单位或向上平移1个单位,我们把这种变换称为抛物线的简单变换.已知抛物线经过两次简单变换后的一条抛物线是y=x2+1,则原抛物线的解析式不可能的是( )
A.y=x2+4x+4 B.y=x2+6x+5 C.y=x2-1 D.y=x2+8x+17
8. 如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m.水面下降2.5m,水面宽度增加( )
A.1m B.2m C.3m D.6m
第8题图
第10题图
第9题图
9. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论有( )
6
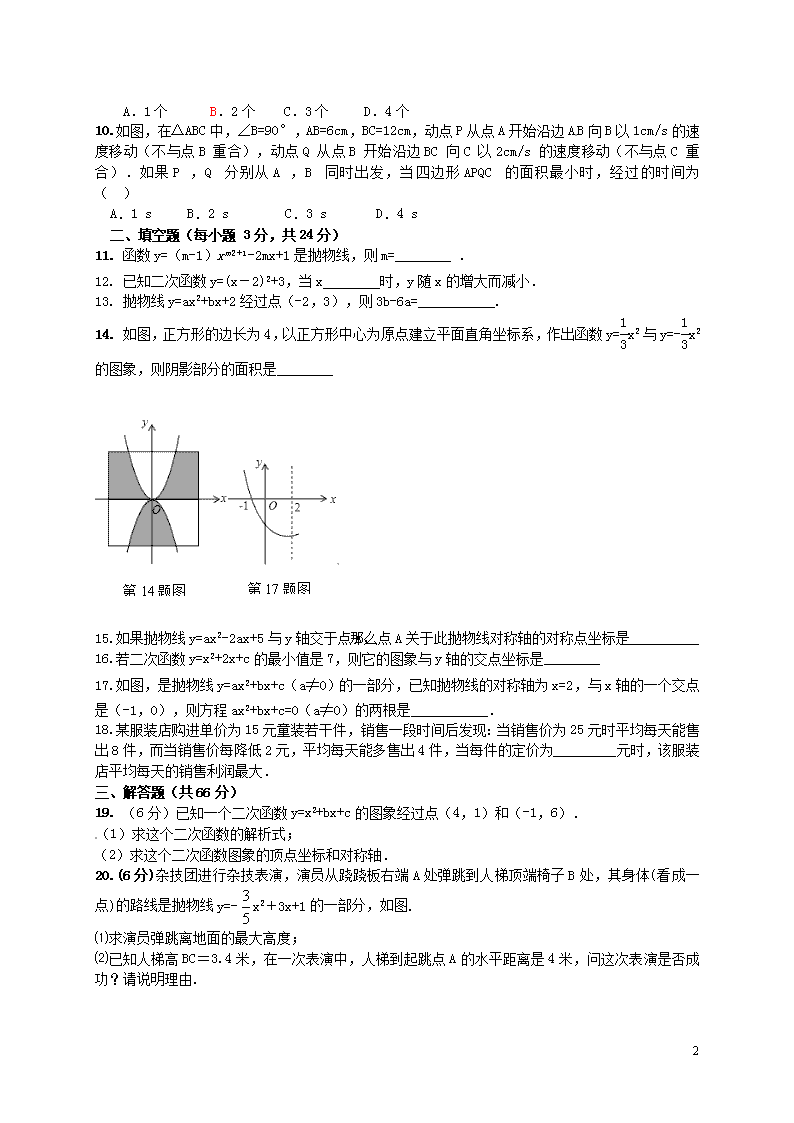
A.1个 B.2个 C.3个 D.4个
10. 如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P,Q分别从A,B同时出发,当四边形APQC的面积最小时,经过的时间为 ( )
A.1 s B.2 s C.3 s D.4 s
二、填空题(每小题 3分,共24分)
11. 函数y=(m-1)xm2+1-2mx+1是抛物线,则m=________ -1
.
12. 已知二次函数y=(x-2)2+3,当x 时,y随x的增大而减小.
13. 抛物线y=ax2+bx+2经过点(-2,3),则3b-6a=___________.
14. 如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数y=x2与y=-x2的图象,则阴影部分的面积是________
第17题图
第14题图
15.如果抛物线y=ax2-2ax+5与y轴交于点A,那么点A关于此抛物线对称轴的对称点坐标是__________
16.若二次函数y=x2+2x+c的最小值是7,则它的图象与y轴的交点坐标是________
17.如图,是抛物线y=ax2+bx+c(a≠0)的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),则方程ax2+bx+c=0(a≠0)的两根是___________.
18.某服装店购进单价为15元童装若干件,销售一段时间后发现:当销售价为25元时平均每天能售出8件,而当销售价每降低2元,平均每天能多售出4件,当每件的定价为_________22
元时,该服装店平均每天的销售利润最大.
三、解答题(共66分)
19. (6分)已知一个二次函数y=x2+bx+c的图象经过点(4,1)和(-1,6).
(1)求这个二次函数的解析式;
(2)求这个二次函数图象的顶点坐标和对称轴.
20.(6分)杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=-x2+3x+1的一部分,如图.
⑴求演员弹跳离地面的最大高度;
⑵已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
6
图5
C
B
A
第20题图
21. (6分)已知二次函数y=x2-2mx+m2+3(m是常数).
(1)求证:不论m为何值,该函数的图象与x轴没有公共点;
(2)把该函数的图象沿y轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点?
22. (6分)如图8,在平面直角坐标系中,正方形OABC的边长为4,顶点A、C分别在x轴、y轴的正半轴,抛物线y=-x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC,BD,CD.
(1)求此抛物线的解析式.
第23题图
(2)求此抛物线顶点D的坐标和四边形ABCD的面积.
第22题图
23.(8分)如图9,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.
24.(8分)为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图10所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)x为何值时,y有最大值?最大值是多少?
6
25.(8分)某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下:
x
30
32
34
36
y
40
36
32
28
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
第26题图
26.(8分)如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=-x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
6
二次函数章末检测题(B)
参考答案
一、1.D 2.D 3.C 4.B 5.A 6.C 7.A 8.B 9.B 10.C
二、11. -1 12. y=-2x2-4x-3. 13. -. 14.8 15. (2,5) 16. (0,8) 17. x1=-1,x2=5
18.22
三、19.解:(1)由题意得,解这个方程组得,
所以所求二次函数的解析式是y=x2-4x+1;
(2)y=x2-4x+1=(x-2)2-3,所以顶点坐标是(2,-3),对称轴是x=2.
20. 解:⑴y=-x2+3x+1=-(x-)2+.
因为-<0,所以函数的最大值是.
⑵当x=4时,y=-×42+3×4+1=3.4=BC,所以这次表演成功.
21.解:(1)证明:因为Δ=(-2m)2-4×1×(m2+3)=4m2-4m2-12=-12<0,所以方程x2-2mx+m2+3=0没有实数解,即不论m为何值,该函数的图象与x轴没有公共点;
(2)解:y=x2-2mx+m2+3=(x-m)2+3,把函数y=(x-m)2+3的图象沿y轴向下平移3个单位长度后,得到函数y=(x-m)2的图象,它的顶点坐标是(m,0),因此,这个函数的图象与x轴只有一个公共点.所以把函数y=x2-2mx+m2+3的图象沿y轴向下平移3个单位长度后,得到的函数的图象与x轴只有一个公共点.
22.解:(1)由已知得:C(0,4),B(4,4),把B与C坐标代入y=-x2+bx+c得,
解得b=2,c=4.则抛物线的解析式为y=-x2+2x+4.
(2) 由y=-x2+2x+4=-(x-2)2+6,得抛物线顶点坐标为(2,6),则S四边形ABDC=S△ABC+
S△BCD=×4×4+×4×2=8+4=12.
23.解:(1)因为二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点,
所以 解得a=,b=-,c=-1.所以二次函数的解析式为y=x2-x-1.
(2)当y=0时,得x2-x-1=0.解得x1=2,x2=-1,∴点D坐标为(-1,0);
6
(3)图象如图,当一次函数的值大于二次函数的值时,x的取值范围是-1<x<4.
24.解:(1)∵三块矩形区域的面积相等,∴矩形AEFD面积是矩形BCFE面积的2倍,∴AE=2BE,
设BE=a,则AE=2a,∴8a+2x=80,∴a=-x+10,3a=-x+30.
∴y=(-x+30)x=-x2+30x.
∵a=-x+10>0,∴x<40,则y=-x2+30x(0<x<40);
(2)∵y=-x2+30x=-(x-20)2+300(0<x<40),且二次项系数为-<0,
∴当x=20时,y有最大值,最大值为300平方米.
25.解:(1)设该函数的解析式为y=kx+b,根据题意,得 ,解得.
故该函数的关系式为y=-2x+100;
(2)根据题意得,(-2x+100)(x-30)=150,解这个方程得,x1=35,x2=45.
故每件商品的销售价定为35元或45元时日利润为150元;
(3)根据题意,得w=(-2x+100)(x-30)=-2x2+160x-3000=-2(x-40)2+200,
∵a=-2<0 则抛物线开口向下,函数有最大值,即当x=40时,w的值最大,
∴当销售单价为40元时获得利润最大.
26.解:(1)根据题意得B(0,4),C(3,),代入关系式y=-x2+bx+c可得
解得b=2,c=4.
∴抛物线关系式为y=-x2+2x+4,即y=-(x-6)2+10,∴D(6,10).
∴拱顶D到地面OA的距离为10m;
(2)由题意得货运汽车最外侧与地面OA的交点为(2,0)或(10,0).
当x=2或x=10时,y=>6,所以这辆货车能安全通过;
(3)令y=8,则-(x-6)2+10=8,解得x1=6+2,x2=6-2,
则x1-x2=4,所以两排灯的水平距离最小是4m.
6
相关文档
- 人教版初中物理中考复习课件-第八2021-11-1125页
- 2019四川省乐山市初中学业水平考试2021-11-1115页
- 2019四川省乐山市初中学业水平考试2021-11-1115页
- 初中物理中考复习单元复习课件:第32021-11-1134页
- 初中数学中考复习课件章节考点专题2021-11-1124页
- 初中道德与法治2020中考模拟试题42021-11-117页
- 初中《道德与法治》九年级下册第三2021-11-1123页
- 初中道德与法治2020年中考考前诊断2021-11-116页
- 滨州市二O二O年初中学业水平考试历2021-11-1114页
- 初中物理中考复习课件:6动态电路分2021-11-1124页