2019年四川省凉山州中考数学试卷含答案 29页

‎2019年四川省凉山州中考数学试卷 一、选择题（共12个小题，每小题4分，共48分）在每小题给出的四个选项中只有一项是正确的，把正确选项的宇母填涂在答题卡上相应的位置 ‎1．（4分）﹣2的相反数是（　　）‎ A．2 B．﹣2 C．‎1‎‎2‎ D．‎‎-‎‎1‎‎2‎ ‎2．（4分）2018年凉山州生产总值约为153300000000，用科学记数法表示数153300000000是（　　）‎ A．1.533×109 B．1.533×1010 C．1.533×1011 D．1.533×1012‎ ‎3．（4分）如图，BD∥EF，AE与BD交于点C，∠B＝30°，∠A＝75°，则∠E的度数为（　　）‎ A．135° B．125° C．115° D．105°‎ ‎4．（4分）下列各式正确的是（　　）‎ A．2a2+3a2＝5a4 B．a2•a＝a3 ‎ C．（a2）3＝a5 D．a‎2‎‎=‎a ‎5．（4分）不等式1﹣x≥x﹣1的解集是（　　）‎ A．x≥1 B．x≥﹣1 C．x≤1 D．x≤﹣1‎ ‎6．（4分）某班40名同学一周参加体育锻炼时间统计如表所示：‎ 人数（人）‎ ‎3‎ ‎17‎ ‎13‎ ‎7‎ 时间（小时）‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是（　　）‎ A．17，8.5 B．17，9 C．8，9 D．8，8.5‎ ‎7．（4分）下列命题：①直线外一点到这条直线的垂线段，叫做点到直线的距离；②两点之间线段最短；③相等的圆心角所对的弧相等；④平分弦的直径垂直于弦．其中，真命题的个数是（　　）‎ A．1 B．2 C．3 D．4‎ ‎8．（4分）如图，正比例函数y＝kx与反比例函数y‎=‎‎4‎x的图象相交于A、C两点，过点A作x轴的垂线交x轴于点B，连接BC，则△ABC的面积等于（　　）‎ A．8 B．6 C．4 D．2‎ ‎9．（4分）如图，在△ABC中，CA＝CB＝4，cosC‎=‎‎1‎‎4‎，则sinB的值为（　　）‎ A．‎10‎‎2‎ B．‎15‎‎3‎ C．‎6‎‎4‎ D．‎‎10‎‎4‎ ‎10．（4分）如图，在△ABC中，D在AC边上，AD：DC＝1：2，O是BD的中点，连接AO并延长交BC于E，则BE：EC＝（　　）‎ A．1：2 B．1：3 C．1：4 D．2：3‎ ‎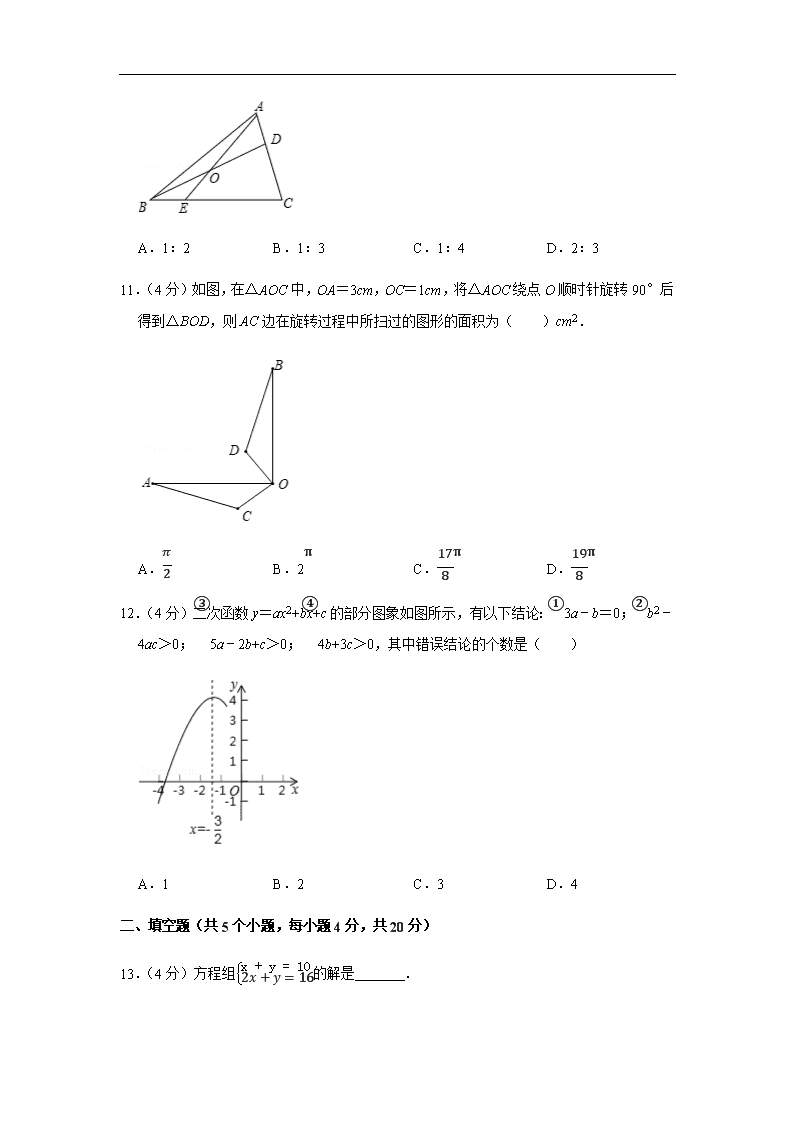11．（4分）如图，在△AOC中，OA＝3cm，OC＝1cm，将△AOC绕点O顺时针旋转90°后得到△BOD，则AC边在旋转过程中所扫过的图形的面积为（　　）cm2．‎ A．π‎2‎ B．2π C．‎17‎‎8‎π D．‎19‎‎8‎π ‎12．（4分）二次函数y＝ax2+bx+c的部分图象如图所示，有以下结论：①3a﹣b＝0；②b2﹣4ac＞0；③5a﹣2b+c＞0；④4b+3c＞0，其中错误结论的个数是（　　）‎ A．1 B．2 C．3 D．4‎ 二、填空题（共5个小题，每小题4分，共20分）‎ ‎13．（4分）方程组x+y=10‎‎2x+y=16‎的解是　 　．‎ ‎14．（4分）方程‎2x-1‎x-1‎‎+‎2‎‎1-‎x‎2‎=‎1的解是　 　．‎ ‎15．（4分）如图所示，AB是⊙O的直径，弦CD⊥AB于H，∠A＝30°，CD＝2‎3‎，则⊙O的半径是　 　．‎ ‎16．（4分）在▱ABCD中，E是AD上一点，且点E将AD分为2：3的两部分，连接BE、AC相交于F，则S△AEF：S△CBF是　 　．‎ ‎17．（4分）将抛物线y＝（x﹣3）2﹣2向左平移　 　个单位后经过点A（2，2）．‎ 三、解答题（共5小题，共32分）‎ ‎18．（5分）计算：tan45°+（‎3‎‎-‎‎2‎）0﹣（‎-‎‎1‎‎2‎）﹣2+|‎3‎‎-‎2|．‎ ‎19．（5分）先化简，再求值：（a+3）2﹣（a+1）（a﹣1）﹣2（2a+4），其中a‎=-‎‎1‎‎2‎．‎ ‎20．（6分）如图，正方形ABCD的对角线AC、BD相交于点O，E是OC上一点，连接EB．过点A作AM⊥BE，垂足为M，AM与BD相交于点F．求证：OE＝OF．‎ ‎21．（8分）某校初中部举行诗词大会预选赛，学校对参赛同学获奖情况进行统计，绘制了如下两幅不完整的统计图．请结合图中相关数据解答下列问题：‎ ‎（1）参加此次诗词大会预选赛的同学共有　 　人；‎ ‎（2）在扇形统计图中，“三等奖”所对应的扇形的圆心角的度数为　 　；‎ ‎（3）将条形统计图补充完整；‎ ‎（4）若获得一等奖的同学中有‎1‎‎4‎来自七年级，‎1‎‎2‎来自九年级，其余的来自八年级，学校决定从获得一等奖的同学中任选两名同学参加全市诗词大会比赛，请通过列表或树状图方法求所选两名同学中，恰好是一名七年级和一名九年级同学的概率．‎ ‎22．（8分）如图，点D是以AB为直径的⊙O上一点，过点B作⊙O的切线，交AD的延长线于点C，E是BC的中点，连接DE并延长与AB的延长线交于点F．‎ ‎（1）求证：DF是⊙O的切线；‎ ‎（2）若OB＝BF，EF＝4，求AD的长．‎ 四、B卷填空题（共2小题，每小题5分，共10分）‎ ‎23．（5分）当0≤x≤3时，直线y＝a与抛物线y＝（x﹣1）2﹣3有交点，则a的取值范围是　 　．‎ ‎24．（5分）如图，正方形ABCD中，AB＝12，AE‎=‎‎1‎‎4‎AB，点P在BC上运动（不与B、C 重合），过点P作PQ⊥EP，交CD于点Q，则CQ的最大值为　 　．‎ 五、解答题（共4小题，共40分）‎ ‎25．（8分）已知二次函数y＝x2+x+a的图象与x轴交于A（x1，0）、B（x2，0）两点，且‎1‎x‎1‎‎2‎‎+‎1‎x‎2‎‎2‎=‎1，求a的值．‎ ‎26．（10分）根据有理数乘法（除法）法则可知：‎ ‎①若ab＞0（或ab‎＞‎0），则a＞0‎b＞0‎或a＜0‎b＜0‎；‎ ‎②若ab＜0（或ab‎＜‎0），则a＞0‎b＜0‎或a＜0‎b＞0‎．‎ 根据上述知识，求不等式（x﹣2）（x+3）＞0的解集 解：原不等式可化为：（1）x-2＞0‎x+3＞0‎或（2）x-2＜0‎x+3＜0‎．‎ 由（1）得，x＞2，‎ 由（2）得，x＜﹣3，‎ ‎∴原不等式的解集为：x＜﹣3或x＞2．‎ 请你运用所学知识，结合上述材料解答下列问题：‎ ‎（1）不等式x2﹣2x﹣3＜0的解集为　 　．‎ ‎（2）求不等式x+4‎‎1-x‎＜‎0的解集（要求写出解答过程）‎ ‎27．（10分）如图，∠ABD＝∠BCD＝90°，DB平分∠ADC，过点B作BM∥CD交AD于M．连接CM交DB于N．‎ ‎（1）求证：BD2＝AD•CD；‎ ‎（2）若CD＝6，AD＝8，求MN的长．‎ ‎28．（12分）如图，抛物线y＝ax2+bx+c的图象过点A（﹣1，0）、B（3，0）、C（0，3）．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在抛物线的对称轴上是否存在一点P，使得△PAC的周长最小，若存在，请求出点P的坐标及△PAC的周长；若不存在，请说明理由；‎ ‎（3）在（2）的条件下，在x轴上方的抛物线上是否存在点M（不与C点重合），使得S△PAM＝S△PAC？若存在，请求出点M的坐标；若不存在，请说明理由．‎ ‎2019年四川省凉山州中考数学试卷 参考答案与试题解析 一、选择题（共12个小题，每小题4分，共48分）在每小题给出的四个选项中只有一项是正确的，把正确选项的宇母填涂在答题卡上相应的位置 ‎1．（4分）﹣2的相反数是（　　）‎ A．2 B．﹣2 C．‎1‎‎2‎ D．‎‎-‎‎1‎‎2‎ ‎【解答】解：根据相反数的定义，﹣2的相反数是2．‎ 故选：A．‎ ‎2．（4分）2018年凉山州生产总值约为153300000000，用科学记数法表示数153300000000是（　　）‎ A．1.533×109 B．1.533×1010 C．1.533×1011 D．1.533×1012‎ ‎【解答】解：‎ 科学记数法表示：153 300 000 000＝1.533×1011‎ 故选：C．‎ ‎3．（4分）如图，BD∥EF，AE与BD交于点C，∠B＝30°，∠A＝75°，则∠E的度数为（　　）‎ A．135° B．125° C．115° D．105°‎ ‎【解答】解：∵∠B＝30°，∠A＝75°，‎ ‎∴∠ACD＝30°+75°＝105°，‎ ‎∵BD∥EF，‎ ‎∴∠E＝∠ACD＝105°．‎ 故选：D．‎ ‎4．（4分）下列各式正确的是（　　）‎ A．2a2+3a2＝5a4 B．a2•a＝a3 ‎ C．（a2）3＝a5 D．a‎2‎‎=‎a ‎【解答】解：A、2a2+3a2＝5a2，故选项A不合题意；‎ B、a2•a＝a3，故选项B符合题意；‎ C、（a2）3＝a6，故选项C不合题意；‎ D、a‎2‎‎=‎|a|，故选项D不合题意．‎ 故选：B．‎ ‎5．（4分）不等式1﹣x≥x﹣1的解集是（　　）‎ A．x≥1 B．x≥﹣1 C．x≤1 D．x≤﹣1‎ ‎【解答】解：1﹣x≥x﹣1，‎ ‎﹣2x≥﹣2‎ ‎∴x≤1．‎ 故选：C．‎ ‎6．（4分）某班40名同学一周参加体育锻炼时间统计如表所示：‎ 人数（人）‎ ‎3‎ ‎17‎ ‎13‎ ‎7‎ 时间（小时）‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是（　　）‎ A．17，8.5 B．17，9 C．8，9 D．8，8.5‎ ‎【解答】解：众数是一组数据中出现次数最多的数，即8；‎ 由统计表可知，处于20，21两个数的平均数就是中位数，‎ ‎∴这组数据的中位数为‎8+9‎‎2‎‎=‎8.5；‎ 故选：D．‎ ‎7．（4分）下列命题：①直线外一点到这条直线的垂线段，叫做点到直线的距离；②两点之间线段最短；③相等的圆心角所对的弧相等；④平分弦的直径垂直于弦．其中，真命题的个数是（　　）‎ A．1 B．2 C．3 D．4‎ ‎【解答】解：①直线外一点到这条直线的垂线段，叫做点到直线的距离；假命题；‎ ‎②两点之间线段最短；真命题；‎ ‎③相等的圆心角所对的弧相等；假命题；‎ ‎④平分弦的直径垂直于弦；假命题；‎ 真命题的个数是1个；‎ 故选：A．‎ ‎8．（4分）如图，正比例函数y＝kx与反比例函数y‎=‎‎4‎x的图象相交于A、C两点，过点A作x轴的垂线交x轴于点B，连接BC，则△ABC的面积等于（　　）‎ A．8 B．6 C．4 D．2‎ ‎【解答】解：因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值，‎ 即S‎=‎‎1‎‎2‎|k|．‎ 所以△ABC的面积等于2‎×‎‎1‎‎2‎|k|＝|k|＝4．‎ 故选：C．‎ ‎9．（4分）如图，在△ABC中，CA＝CB＝4，cosC‎=‎‎1‎‎4‎，则sinB的值为（　　）‎ A．‎10‎‎2‎ B．‎15‎‎3‎ C．‎6‎‎4‎ D．‎‎10‎‎4‎ ‎【解答】解：过点A作AD⊥BC，垂足为D，如图所示．‎ 在Rt△ACD中，CD＝CA•cosC＝1，‎ ‎∴AD‎=AD‎2‎-CD‎2‎=‎‎15‎；‎ 在Rt△ABD中，BD＝CB﹣CD＝3，AD‎=‎‎15‎，‎ ‎∴AB‎=BD‎2‎+AD‎2‎=‎2‎6‎，‎ ‎∴sinB‎=ADAB=‎‎10‎‎4‎．‎ 故选：D．‎ ‎10．（4分）如图，在△ABC中，D在AC边上，AD：DC＝1：2，O是BD的中点，连接AO并延长交BC于E，则BE：EC＝（　　）‎ A．1：2 B．1：3 C．1：4 D．2：3‎ ‎【解答】解：如图，过O作OG∥BC，交AC于G，‎ ‎∵O是BD的中点，‎ ‎∴G是DC的中点．‎ 又AD：DC＝1：2，‎ ‎∴AD＝DG＝GC，‎ ‎∴AG：GC＝2：1，AO：OE＝2：1，‎ ‎∴S△AOB：S△BOE＝2‎ 设S△BOE＝S，S△AOB＝2S，又BO＝OD，‎ ‎∴S△AOD＝2S，S△ABD＝4S，‎ ‎∵AD：DC＝1：2，‎ ‎∴S△BDC＝2S△ABD＝8S，S四边形CDOE＝7S，‎ ‎∴S△AEC＝9S，S△ABE＝3S，‎ ‎∴‎BEEC‎=S‎△ABES‎△AEC=‎3S‎9S=‎‎1‎‎3‎ 故选：B．‎ ‎11．（4分）如图，在△AOC中，OA＝3cm，OC＝1cm，将△AOC绕点O顺时针旋转90°后得到△BOD，则AC边在旋转过程中所扫过的图形的面积为（　　）cm2．‎ A．π‎2‎ B．2π C．‎17‎‎8‎π D．‎19‎‎8‎π ‎【解答】解：∵△AOC≌△BOD，‎ ‎∴阴影部分的面积＝扇形OAB的面积﹣扇形OCD的面积‎=‎90⋅π×‎‎3‎‎2‎‎360‎-‎90⋅π×‎‎1‎‎2‎‎360‎=‎2π，‎ 故选：B．‎ ‎12．（4分）二次函数y＝ax2+bx+c的部分图象如图所示，有以下结论：①3a﹣b＝0；②b2﹣4ac＞0；③5a﹣2b+c＞0；④4b+3c＞0，其中错误结论的个数是（　　）‎ A．1 B．2 C．3 D．4‎ ‎【解答】解：由图象可知a＜0，c＞0，对称轴为x‎=-‎‎3‎‎2‎，‎ ‎∴x‎=-‎3‎‎2‎=-‎b‎2a，‎ ‎∴b＝3a，‎ ‎①正确；‎ ‎∵函数图象与x轴有两个不同的交点，‎ ‎∴△＝b2﹣4ac＞0，‎ ‎②正确；‎ 当x＝﹣1时，a﹣b+c＞0，‎ 当x＝﹣3时，9a﹣3b+c＞0，‎ ‎∴10a﹣4b+2c＞0，‎ ‎∴5a﹣2b+c＞0，‎ ‎③正确；‎ 由对称性可知x＝1时对应的y值与x＝﹣4时对应的y值相等，‎ ‎∴当x＝1时a+b+c＜0，‎ ‎∵b＝3a，‎ ‎∴4b+3c＝3b+b+3c＝3b+3a+3c＝3（a+b+c）＜0，‎ ‎∴4b+3c＜0，‎ ‎④错误；‎ 故选：A．‎ 二、填空题（共5个小题，每小题4分，共20分）‎ ‎13．（4分）方程组x+y=10‎‎2x+y=16‎的解是　x=6‎y=4‎　．‎ ‎【解答】解：x+y=10‎‎①‎‎2x+y=16‎‎②‎，‎ ‎②﹣①得：‎ x＝6，‎ 把x＝6代入①得：‎ ‎6+y＝10，‎ 解得：y＝4，‎ 方程组的解为：x=6‎y=4‎，‎ 故答案为：x=6‎y=4‎．‎ ‎14．（4分）方程‎2x-1‎x-1‎‎+‎2‎‎1-‎x‎2‎=‎1的解是　x＝﹣2　．‎ ‎【解答】解：‎‎2x-1‎x-1‎‎-‎2‎‎(x+1)(x-1)‎=1‎ 去分母，得（2x﹣1）（x+1）﹣2＝（x+1）（x﹣1）‎ 去括号，得2x2+x﹣3＝x2﹣1‎ 移项并整理，得x2+x﹣2＝0‎ 所以（x+2）（x﹣1）＝0‎ 解得x＝﹣2或x＝1‎ 经检验，x＝﹣2是原方程的解．‎ 故答案为：x＝﹣2．‎ ‎15．（4分）如图所示，AB是⊙O的直径，弦CD⊥AB于H，∠A＝30°，CD＝2‎3‎，则⊙O的半径是　2　．‎ ‎【解答】解：连接BC，如图所示：‎ ‎∵AB是⊙O的直径，弦CD⊥AB于H，‎ ‎∴∠ACB＝90°，CH＝DH‎=‎‎1‎‎2‎CD‎=‎‎3‎，‎ ‎∵∠A＝30°，‎ ‎∴AC＝2CH＝2‎3‎，‎ 在Rt△ABC中，∠A＝30°，‎ ‎∴AC‎=‎‎3‎BC＝2‎3‎，AB＝2BC，‎ ‎∴BC＝2，AB＝4，‎ ‎∴OA＝2，‎ 即⊙O的半径是2；‎ 故答案为：2．‎ ‎16．（4分）在▱ABCD中，E是AD上一点，且点E将AD分为2：3的两部分，连接BE、AC相交于F，则S△AEF：S△CBF是　4：25或9：25　．‎ ‎【解答】解：①当AE：ED＝2：3时，‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴AD∥BC，AE：BC＝2：5，‎ ‎∴△AEF∽△CBF，‎ ‎∴S△AEF：S△CBF＝（‎2‎‎5‎）2＝4：25；‎ ‎②当AE：ED＝3：2时，‎ 同理可得，S△AEF：S△CBF＝（‎3‎‎5‎）2＝9：25，‎ 故答案为：4：25或9：25．‎ ‎17．（4分）将抛物线y＝（x﹣3）2﹣2向左平移　3　个单位后经过点A（2，2）．‎ ‎【解答】解：∵将抛物线y＝（x﹣3）2﹣2向左平移后经过点A（2，2），‎ ‎∴设平移后解析式为：y＝（x﹣3+a）2﹣2，‎ 则2＝（2﹣3+a）2﹣2，‎ 解得：a＝3或a＝﹣1（不合题意舍去），‎ 故将抛物线y＝（x﹣3）2﹣2向左平移3个单位后经过点A（2，2）．‎ 故答案为：3．‎ 三、解答题（共5小题，共32分）‎ ‎18．（5分）计算：tan45°+（‎3‎‎-‎‎2‎）0﹣（‎-‎‎1‎‎2‎）﹣2+|‎3‎‎-‎2|．‎ ‎【解答】解：原式＝1+1﹣4+（2‎-‎‎3‎）‎=-‎‎3‎．‎ ‎19．（5分）先化简，再求值：（a+3）2﹣（a+1）（a﹣1）﹣2（2a+4），其中a‎=-‎‎1‎‎2‎．‎ ‎【解答】解：‎ 原式＝a2+6a+9﹣（a2﹣1）﹣4a﹣8‎ ‎＝2a+2‎ 将a‎=-‎‎1‎‎2‎代入原式＝2×（‎-‎‎1‎‎2‎）+2＝1‎ ‎20．（6分）如图，正方形ABCD的对角线AC、BD相交于点O，E是OC上一点，连接EB．过点A作AM⊥BE，垂足为M，AM与BD相交于点F．求证：OE＝OF．‎ ‎【解答】证明：∵四边形ABCD是正方形．‎ ‎∴∠BOE＝∠AOF＝90°，OB＝OA．‎ 又∵AM⊥BE，‎ ‎∴∠MEA+∠MAE＝90°＝∠AFO+∠MAE，‎ ‎∴∠MEA＝∠AFO．‎ ‎∴△BOE≌△AOF（AAS）．‎ ‎∴OE＝OF．‎ ‎21．（8分）某校初中部举行诗词大会预选赛，学校对参赛同学获奖情况进行统计，绘制了如下两幅不完整的统计图．请结合图中相关数据解答下列问题：‎ ‎（1）参加此次诗词大会预选赛的同学共有　40　人；‎ ‎（2）在扇形统计图中，“三等奖”所对应的扇形的圆心角的度数为　90°　；‎ ‎（3）将条形统计图补充完整；‎ ‎（4）若获得一等奖的同学中有‎1‎‎4‎来自七年级，‎‎1‎‎2‎ 来自九年级，其余的来自八年级，学校决定从获得一等奖的同学中任选两名同学参加全市诗词大会比赛，请通过列表或树状图方法求所选两名同学中，恰好是一名七年级和一名九年级同学的概率．‎ ‎【解答】解：（1）参加此次诗词大会预选赛的同学共有18÷45%＝40（人），‎ 故答案为：40；‎ ‎（2）扇形统计图中获三等奖的圆心角为360°‎×‎10‎‎40‎=‎90°，‎ 故答案为：90°．‎ ‎（3）获二等奖的人数＝40×20%＝8，一等奖的人数为40﹣8﹣10﹣18＝4（人），‎ 条形统计图为：‎ ‎（4）由题意知，获一等奖的学生中，七年级有1人，八年级有1人，九年级有2人，‎ 画树状图为：（用A、B、C分别表示七年级、八年级和九年级的学生）‎ 共有12种等可能的结果数，其中所选出的两人中既有七年级又有九年级同学的结果数为4，‎ 所以所选出的两人中既有七年级又有九年级同学的概率‎4‎‎12‎‎=‎‎1‎‎3‎．‎ ‎22．（8分）如图，点D是以AB为直径的⊙O上一点，过点B作⊙O的切线，交AD的延长线于点C，E是BC的中点，连接DE并延长与AB的延长线交于点F．‎ ‎（1）求证：DF是⊙O的切线；‎ ‎（2）若OB＝BF，EF＝4，求AD的长．‎ ‎【解答】解：（1）如图，连接OD，BD，‎ ‎∵AB为⊙O的直径，‎ ‎∴∠ADB＝∠BDC＝90°，‎ 在Rt△BDC中，∵BE＝EC，‎ ‎∴DE＝EC＝BE，‎ ‎∴∠1＝∠3，‎ ‎∵BC是⊙O的切线，‎ ‎∴∠3+∠4＝90°，‎ ‎∴∠1+∠4＝90°，‎ 又∵∠2＝∠4，‎ ‎∴∠1+∠2＝90°，‎ ‎∴DF为⊙O的切线；‎ ‎（2）∵OB＝BF，‎ ‎∴OF＝2OD，‎ ‎∴∠F＝30°，‎ ‎∵∠FBE＝90°，‎ ‎∴BE‎=‎‎1‎‎2‎EF＝2，‎ ‎∴DE＝BE＝2，‎ ‎∴DF＝6，‎ ‎∵∠F＝30°，∠ODF＝90°，‎ ‎∴∠FOD＝60°，‎ ‎∵OD＝OA，‎ ‎∴∠A＝∠ADO‎=‎1‎‎2‎∠‎BOD＝30°，‎ ‎∴∠A＝∠F，‎ ‎∴AD＝DF＝6．‎ 四、B卷填空题（共2小题，每小题5分，共10分）‎ ‎23．（5分）当0≤x≤3时，直线y＝a与抛物线y＝（x﹣1）2﹣3有交点，则a的取值范围是　﹣3≤a≤1　．‎ ‎【解答】解：‎ 法一：y＝a与抛物线y＝（x﹣1）2﹣3有交点 则有a＝（x﹣1）2﹣3，整理得x2﹣2x﹣2﹣a＝0‎ ‎∴△＝b2﹣4ac＝4+4（2+a）≥0‎ 解得a≥﹣3，‎ ‎∵0≤x≤3，对称轴x＝1‎ ‎∴y＝（3﹣1）2﹣3＝1‎ ‎∴a≤1‎ 法二：由题意可知，‎ ‎∵抛物线的 顶点为（1，﹣3），而0≤x≤3‎ ‎∴抛物线y的取值为﹣3≤y≤1‎ ‎∵y＝a，则直线y与x轴平行，‎ ‎∴要使直线y＝a与抛物线y＝（x﹣1）2﹣3有交点，‎ ‎∴抛物线y的取值为﹣3≤y≤1，即为a的取值范围，‎ ‎∴﹣3≤a≤1‎ 故答案为：﹣3≤a≤1‎ ‎24．（5分）如图，正方形ABCD中，AB＝12，AE‎=‎‎1‎‎4‎AB，点P在BC上运动（不与B、C重合），过点P作PQ⊥EP，交CD于点Q，则CQ的最大值为　4　．‎ ‎【解答】解：∵∠BEP+∠BPE＝90°，∠QPC+∠BPE＝90°，‎ ‎∴∠BEP＝∠CPQ．‎ 又∠B＝∠C＝90°，‎ ‎∴△BPE∽△CQP．‎ ‎∴BEPC‎=‎BPCQ．‎ 设CQ＝y，BP＝x，则CP＝12﹣x．‎ ‎∴‎9‎‎12-x‎=‎xy，化简得y‎=-‎‎1‎‎9‎（x2﹣12x），‎ 整理得y‎=-‎‎1‎‎9‎（x﹣6）2+4，‎ 所以当x＝6时，y有最大值为4．‎ 故答案为4．‎ 五、解答题（共4小题，共40分）‎ ‎25．（8分）已知二次函数y＝x2+x+a的图象与x轴交于A（x1，0）、B（x2，0）两点，且‎1‎x‎1‎‎2‎‎+‎1‎x‎2‎‎2‎=‎1，求a的值．‎ ‎【解答】解：y＝x2+x+a的图象与x轴交于A（x1，0）、B（x2，0）两点，‎ ‎∴x1+x2＝﹣1，x1•x2＝a，‎ ‎∵‎1‎x‎1‎‎2‎‎+‎1‎x‎2‎‎2‎=x‎1‎‎2‎‎+‎x‎2‎‎2‎x‎1‎‎2‎x‎2‎‎2‎=‎(x‎1‎+x‎2‎‎)‎‎2‎-2‎x‎1‎x‎2‎‎(x‎1‎x‎2‎‎)‎‎2‎=‎1-2aa‎2‎=‎1，‎ ‎∴a＝﹣1‎+‎‎2‎或a＝﹣1‎-‎‎2‎；‎ ‎∵△＝1﹣4a＞0，‎ ‎∴a‎＜‎‎1‎‎4‎，‎ ‎∴a＝﹣1‎-‎‎2‎；‎ ‎26．（10分）根据有理数乘法（除法）法则可知：‎ ‎①若ab＞0（或ab‎＞‎0），则a＞0‎b＞0‎或a＜0‎b＜0‎；‎ ‎②若ab＜0（或ab‎＜‎0），则a＞0‎b＜0‎或a＜0‎b＞0‎．‎ 根据上述知识，求不等式（x﹣2）（x+3）＞0的解集 解：原不等式可化为：（1）x-2＞0‎x+3＞0‎或（2）x-2＜0‎x+3＜0‎．‎ 由（1）得，x＞2，‎ 由（2）得，x＜﹣3，‎ ‎∴原不等式的解集为：x＜﹣3或x＞2．‎ 请你运用所学知识，结合上述材料解答下列问题：‎ ‎（1）不等式x2﹣2x﹣3＜0的解集为　﹣1＜x＜3　．‎ ‎（2）求不等式x+4‎‎1-x‎＜‎0的解集（要求写出解答过程）‎ ‎【解答】解：（1）原不等式可化为：①x-3＞0‎x+1＜0‎或②x-3＜0‎x+1＞0‎．‎ 由①得，空集，‎ 由②得，﹣1＜x＜3，‎ ‎∴原不等式的解集为：﹣1＜x＜3，‎ 故答案为：﹣1＜x＜3．‎ ‎（2）由x+4‎‎1-x‎＜‎0知①x+4＞0‎‎1-x＜0‎或②x+4＜0‎‎1-x＞0‎，‎ 解不等式组①，得：x＞1；‎ 解不等式组②，得：x＜﹣4；‎ 所以不等式x+4‎‎1-x‎＜‎0的解集为x＞1或x＜﹣4．‎ ‎27．（10分）如图，∠ABD＝∠BCD＝90°，DB平分∠ADC，过点B作BM∥CD交AD于M．连接CM交DB于N．‎ ‎（1）求证：BD2＝AD•CD；‎ ‎（2）若CD＝6，AD＝8，求MN的长．‎ ‎【解答】证明：（1）∵DB平分∠ADC，‎ ‎∴∠ADB＝∠CDB，且∠ABD＝∠BCD＝90°，‎ ‎∴△ABD∽△BCD ‎∴‎ADBD‎=‎BDCD ‎∴BD2＝AD•CD ‎（2）∵BM∥CD ‎∴∠MBD＝∠BDC ‎∴∠ADB＝∠MBD，且∠ABD＝90°‎ ‎∴BM＝MD，∠MAB＝∠MBA ‎∴BM＝MD＝AM＝4‎ ‎∵BD2＝AD•CD，且CD＝6，AD＝8，‎ ‎∴BD2＝48，‎ ‎∴BC2＝BD2﹣CD2＝12‎ ‎∴MC2＝MB2+BC2＝28‎ ‎∴MC＝2‎‎7‎ ‎∵BM∥CD ‎∴△MNB∽△CND ‎∴BMCD‎=MNCN=‎‎2‎‎3‎，且MC＝2‎‎7‎ ‎∴MN‎=‎‎4‎‎5‎‎7‎ ‎28．（12分）如图，抛物线y＝ax2+bx+c的图象过点A（﹣1，0）、B（3，0）、C（0，3）．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在抛物线的对称轴上是否存在一点P，使得△PAC的周长最小，若存在，请求出点P的坐标及△PAC的周长；若不存在，请说明理由；‎ ‎（3）在（2）的条件下，在x轴上方的抛物线上是否存在点M（不与C点重合），使得S△PAM＝S△PAC？若存在，请求出点M的坐标；若不存在，请说明理由．‎ ‎【解答】解：（1）∵抛物线与x轴交于点A（﹣1，0）、B（3，0）‎ ‎∴可设交点式y＝a（x+1）（x﹣3）‎ 把点C（0，3）代入得：﹣3a＝3‎ ‎∴a＝﹣1‎ ‎∴y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3‎ ‎∴抛物线解析式为y＝﹣x2+2x+3‎ ‎（2）在抛物线的对称轴上存在一点P，使得△PAC的周长最小．‎ 如图1，连接PB、BC ‎∵点P在抛物线对称轴直线x＝1上，点A、B关于对称轴对称 ‎∴PA＝PB ‎∴C△PAC＝AC+PC+PA＝AC+PC+PB ‎∵当C、P、B在同一直线上时，PC+PB＝CB最小 ‎∵A（﹣1，0）、B（3，0）、C（0，3）‎ ‎∴AC‎=‎1‎‎2‎‎+‎‎3‎‎2‎=‎‎10‎，BC‎=‎3‎‎2‎‎+‎‎3‎‎2‎=3‎‎2‎ ‎∴C△PAC＝AC+CB‎=‎10‎+3‎‎2‎最小 设直线BC解析式为y＝kx+3‎ 把点B代入得：3k+3＝0，解得：k＝﹣1‎ ‎∴直线BC：y＝﹣x+3‎ ‎∴yP＝﹣1+3＝2‎ ‎∴点P（1，2）使△PAC的周长最小，最小值为‎10‎‎+3‎‎2‎．‎ ‎（3）存在满足条件的点M，使得S△PAM＝S△PAC．‎ ‎∵S△PAM＝S△PAC ‎∴当以PA为底时，两三角形等高 ‎∴点C和点M到直线PA距离相等 ‎①若点M在点P上方，如图2，‎ ‎∴CM∥PA ‎∵A（﹣1，0），P（1，2），设直线AP解析式为y＝px+d ‎∴‎-p+d=0‎p+d=2‎ 解得：‎p=1‎d=1‎ ‎∴直线AP：y＝x+1‎ ‎∴直线CM解析式为：y＝x+3‎ ‎∵y=x+3‎y=-x‎2‎+2x+3‎ 解得：x‎1‎‎=0‎y‎1‎‎=3‎（即点C），‎x‎2‎‎=1‎y‎2‎‎=4‎ ‎∴点M坐标为（1，4）‎ ‎②若点M在点P下方，如图3，‎ 则点M所在的直线l∥PA，且直线l到PA的距离等于直线y＝x+3到PA的距离 ‎∴直线AP：y＝x+1向下平移2个单位得y＝x﹣1即为直线l的解析式 ‎∵y=x-1‎y=-x‎2‎+2x+3‎ 解得：x‎1‎‎=‎‎1+‎‎17‎‎2‎y‎1‎‎=‎‎17‎‎-1‎‎2‎ ‎x‎2‎‎=‎‎1-‎‎17‎‎2‎y‎2‎‎=‎‎-1-‎‎17‎‎2‎ ‎∵点M在x轴上方 ‎∴y＞0‎ ‎∴点M坐标为（‎1+‎‎17‎‎2‎，‎17‎‎-1‎‎2‎）‎ 综上所述，点M坐标为（1，4）或（‎1+‎‎17‎‎2‎，‎17‎‎-1‎‎2‎）时，S△PAM＝S△PAC．‎ 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/6/30 9:59:50；用户：中考培优辅导；邮箱：p5193@xyh.com；学号：27411521‎