人教版中考数学二轮复习专题练习上常用辅助线-构造等边三角形 29页

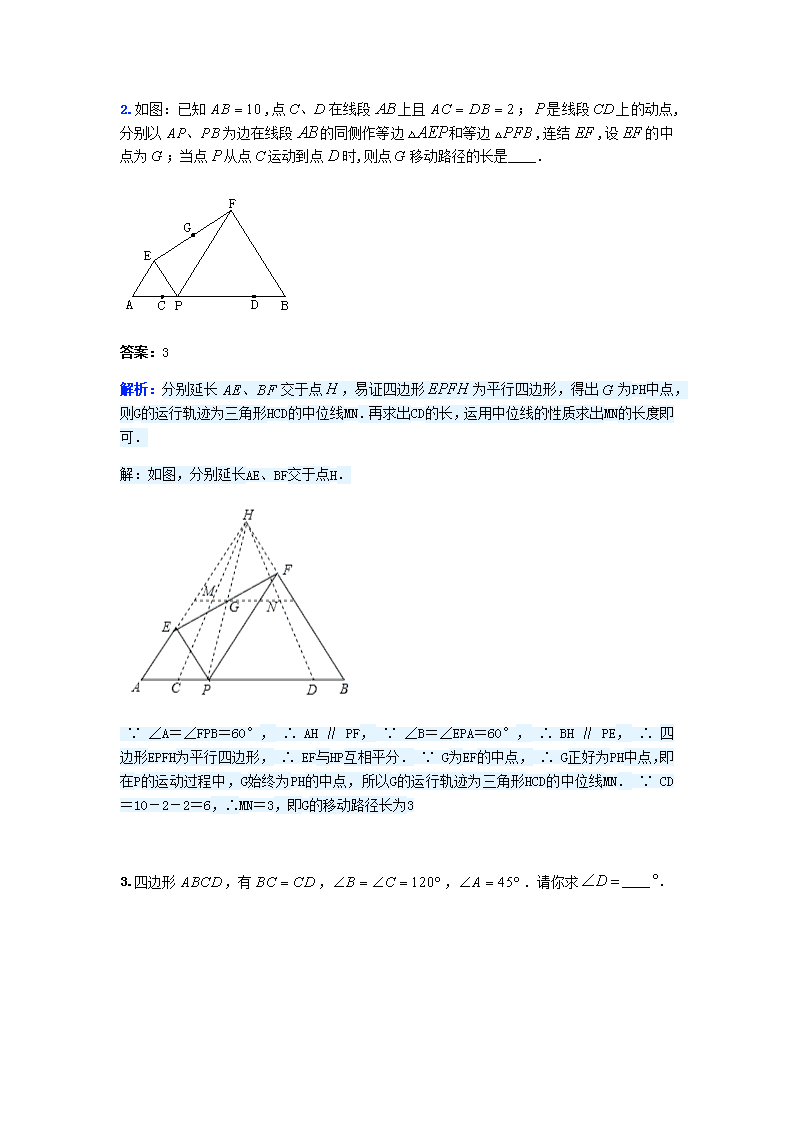
‎6.构造等边三角形 ‎1.公园里有一块形如四边形的草地，测得米，，．请你求出这块草地的面积？‎ 答案：见解析 解析：‎ 延长交于，连结，‎ ‎∵，∴，‎ ‎∴是等边三角形，‎ ‎∵，∴，‎ ‎∴，，‎ ‎∵，∴，‎ ‎∴，，‎ ‎∴这块草地的面积为平方米．‎ ‎2.如图：已知,点在线段上且；是线段上的动点,分别以为边在线段的同侧作等边和等边,连结,设的中点为；当点从点运动到点时,则点移动路径的长是____．‎ 答案：3 ‎ 解析：分别延长交于点，易证四边形为平行四边形，得出为PH中点，则G的运行轨迹为三角形HCD的中位线MN．再求出CD的长，运用中位线的性质求出MN的长度即可．‎ 解：如图，分别延长AE、BF交于点H．‎ ‎∵∠A＝∠FPB＝60°‎‎，‎∴AH∥PF，‎∵∠B＝∠EPA＝60°‎，‎∴BH∥PE，‎∴‎四边形EPFH为平行四边形，‎∴EF与HP互相平分．‎∵G为EF的中点，‎∴G正好为PH中点，即在P的运动过程中，G始终为PH的中点，所以G的运行轨迹为三角形HCD的中位线MN．‎∵CD＝10－2－2＝6‎，∴MN＝3‎，即G的移动路径长为‎3‎ ‎3.四边形，有，，．请你求____.‎ 答案：75‎ 解析：‎ 延长交于，连结，‎ ‎∵，∴，‎ ‎∴是等边三角形，‎ ‎∵，∴，‎ ‎∴，‎ ‎∵，∴，‎ ‎∴ ‎ ‎4.如图，四边形 中， 是对角线， 是等边三角形． ，则 的长为____.‎ 答案：4‎ 解析：首先以为边作等边，连接，利用全等三角形的判定得出 ，进而求出 的长即可．‎ 解：如图，以为边作等边，连接 ‎ ，‎ ‎ 在 和 中，‎ ‎ ‎ ‎ ，‎ ‎ ．‎ 又 ，‎ ‎ ．‎ 在 中， ，‎ 于是 ，‎ ‎．‎ ‎5.如图所示，在中，是内两点，平分，若，则的长度是__.‎ 答案：8‎ 解析：作出辅助线后根据等腰三角形的性质得出，进而得出 为等边三角形， 为等边三角形，从而得出 的长，进而求出答案．‎ 解：延长 交 于 ，延长 交 于 ，作 于 ，‎ 平分 ，‎ ‎ ，‎ ‎ ，‎ 为等边三角形，‎ 为等边三角形，‎ ‎ ，‎ ‎ ，‎ ‎ 为等边三角形，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎6.如图，六边形 中，每一个内角都是．求这个六边形的周长为_____.‎ 答案：116‎ 解析：凸六边形，并不是一规则的六边形，但六个角都是 ，所以通过适当的向外作延长线，可得到等边三角形，进而求解．‎ 解：如图，分别作直线 的延长线和反向延长线使它们交于点 ．‎ ‎ 六边形 的六个角都是120°，‎ ‎ 六边形 的每一个外角的度数都是60°．‎ ‎ 都是等边三角形．‎ ‎ ．‎ ‎．‎ ‎ 六边形的周长为： ．‎ ‎7.如图，已知 ， 平分 ，若 ，则 的长是_____.‎ 答案：5‎ 解析：在 的延长线上取点 ，使 ，连接 ，则可证得 为等边三角形，再结合条件可证明 ，可得 ，再利用线段的和差可求得 ，则可求得 .‎ 解：在 的延长线上取点 ，使 ，连接，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ 为等边三角形，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ 平分 ，‎ ‎ ，‎ ‎ ，‎ 在 和 中，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎8.如图，在 中， 是 内两点， 平分 ，若 ，则 ____．‎ 答案：62‎ 解析：作出辅助线后根据等腰三角形的性质得出 ，进而得出 为等边三角形， 为等边三角形，从而得出 的长，进而求出答案．‎ 解：延长 交 于 ，延长 交 于 ，作 ，‎ ‎ ， 平分 ，‎ ‎ ，‎ ‎ ，‎ ‎ 为等边三角形，‎ ‎ 为等边三角形，‎ ‎ ，‎ ‎ ，‎ ‎ 为等边三角形，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ 故答案为62．‎ ‎9.如图，过边长为的等边 的边 上一点 ，作 于 为 延长线上一点，当 时，连 交 边于 ，则的长为____.（注：若答案不是整数，请化为小数）‎ 答案：0.5‎ 解析：过 作 交 于 ，得出等边三角形 ，推出 ，根据等腰三角形性质求出 ，证 ，推出 ，推出即可．‎ 解：过 作 交 于．‎ ‎ ， 是等边三角形，‎ ‎ 是等边三角形，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ．‎ ‎ 在 和 中，‎ ‎，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ．‎ ‎10.如图， 中， 平分 是 内两点，且 ，若 ，则_____.‎ 答案：10‎ 解析：延长 交 于 ，延长 交 于 ，根据等腰三角形的性质得出 ，进而得出 为等边三角形，从而得出 的长，进而求出答案．‎ 解：延长交 于 ，延长 交 于 ，‎ ‎ 平分 ，‎ ‎ ，‎ ‎ ，‎ ‎ 为等边三角形，‎ ‎ ，‎ ‎ ，‎ ‎ 为等边三角形，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ‎ ‎ ．‎ 故答案为：10．‎ ‎11.如图，凸四边形 满足条件： 那么 ____．（填“大于”或“小于”或“等于”）‎ 答案：等于 解析：延长 到点 ，使得 ，连接 和 ，根据已知条件和所作辅助线可得 与 均为等边三角形，证明 和 全等即可证明；‎ 解：延长 到点 ，使得 ，连接 和.‎ ‎∵‎ ‎∴‎ 又 ，‎ ‎ 与 均为等边三角形 ‎ ‎ ‎ ,即 ‎ 在 和 中 ‎，‎ ‎∴ ‎ ‎∴‎ ‎∵ ‎ ‎ ．‎ 故答案为：相等 ‎12.已知：如图，等边 中， 是 边上一动点，作 ，垂足为 ；作 ，垂足为 ；作 ，垂足为 ．‎ ‎（1）设 ，求 与 之间的函数关系式；‎ ‎（2）当点 和点 重合时，求线段 的长；‎ ‎（3）当点 和点不重合，但线段 延长线相交时，求它们与线段 围成的三角形周长的取值范围．‎ 答案：见解析 解析：（1）由已知等边 中，可得每个角都是 ，由作 ，垂足为 ；作 ，垂足为 ；作 ，垂足为 ，得三个直角三角形且都有 的角，据此用 可表示出 ，相继表示出 ，求出与之间的函数关系式．‎ ‎（2）由已知可列出方程组结合已知求出 的长．‎ ‎（3）当线段 相交时，根据已知得到它们与线段围成的三角形三个角都是 ‎ 解：（1） 是等边三角形， ．‎ ‎ ．‎ 又 ．‎ ‎ ，．‎ ‎ ，‎ ‎ ．‎ ‎（2）由方程组 ‎ 得 ．‎ ‎ 当点和点重合时，，‎ ‎ ．‎ ‎（3）设线段 的延长线相交于点 ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ 是等边三角形，‎ 且当点和点 重合时， 最短为.‎ 且当点和点 重合时， 最长为 ‎ ．‎ ‎13.如图，在四边形 中， ，连接 交于点 ．‎ ‎（1）若 ， 为线段 上一点，且 ，连接 ，求点 到 的距离．‎ ‎（2）证明： ．‎ 答案：见解析 解析：（1）由条件可以证明，可以得出 ， ，求出 ，由勾股定理可以求出 ，由 可以求得 的值，在 中由勾股定理可以求出 的值，从而求出 的值，过点 作 于 ，利用三角形的面积相等建立等量关系就可以求出结论．‎ ‎（2）要证 ，延长 到 ，使 ，则求 即可．由 ，得 是等边三角形，进而得 又有 ，则 是等边三角形，所以得 ，则 ．‎ 解：（1） ，‎ ‎ 是等边三角形，‎ ‎ ．‎ ‎ ，‎ ‎ ，‎ ‎ ．‎ ‎ ，‎ ‎， ．‎ ‎ ，‎ ‎， ，‎ ‎ ，在 中由勾股定理得 ‎ ‎ 过点 作 于点 ．‎ ‎ ．‎ ‎ ，‎ ‎ ．‎ 即点 到 的距离．‎ ‎（2）证明：延长 到点 ，使 ，连接 ， ，‎ ‎ 是等边三角形，‎ ‎ ，‎ ‎ ，‎ ‎ ．‎ ‎ ，‎ ‎ ，‎ ‎ 是等边三角形，‎ ‎ ，‎ ‎ ，‎ 又 ，‎ ‎ ，‎ ‎ ，‎ 即 ．‎ ‎14.已知：如图，在等边三角形 中，点 是 边上的一个动点（ 与 不重合），延长 到 ，使 ，连接 交 于点 ．‎ ‎（1）求证： ；‎ ‎（2）若 的边长为 ，设 ，求 与 的函数关系式，写出自变量的取值范围．‎ 答案：见解析 解析：（1）过 作 交 于 ，则 为等边三角形，得 ，而 ，得到 ，易证得 ，根据全等三角形的性质即可得到结论；‎ ‎（2）由（1）得 ，得到 ，易得 ，而 ，即有 ，即可得到 与 间的函数关系式．‎ 解：（1）证明：过 作 交 于，‎ ‎ ，‎ 又∵在等边三角形 中， ，‎ ‎ ，‎ ‎ 是等边三角形，‎ ‎ ，‎ 又 ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ 在 和 中，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ； ‎ ‎（2）由（1）得 ，‎ ‎ ，‎ 由（1）得 是等边三角形，‎ ‎ ，‎ 又 ，‎ ‎ ，‎ 即．‎ ‎15.如图，在四边形 中， ．‎ ‎（1）求 的度数．‎ ‎（2）求四边形 的面积．‎ 答案：见解析 解析：（1）连接 ，根据 ，得出 是等边三角形，求得 ，然后根据勾股定理的逆定理判断三角形 是直角三角形，从而求得 ；‎ ‎（2）根据四边形的面积等于三角形 和三角形 的和即可求得；‎ 解：（1）连接 ，‎ ‎ ，‎ ‎ 是等边三角形，‎ ‎，‎ ‎ ，‎ 则 ，‎ ‎ ，‎ ‎ ，‎ ‎ ；‎ ‎（2）．‎ ‎16.已知：如图，四边形 中， ．‎ ‎（1）连接 的形状是？‎ ‎（2）求证： ．‎ 答案：见解析 解析：（1）根据全等三角形的判定定理“有一内角为 的等腰三角形是等边三角形”推知 是等边三角形．‎ ‎（2）如图，以 为边向形外作等边 ，连接 ．构造全等三角形（ ），然后根据全等三角形的性质、勾股定理证得结论．‎ 解：（1）如图，连接 ．‎ ‎ ，‎ ‎ 是等边三角形；‎ 故答案是：等边三角形；‎ ‎（2）如图，以 为边向形外作等边，连接．‎ 由（1）知，是等边三角形，‎ 则 ，‎ 在 与 ，‎ ‎∵ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ 在 中，有 ，即 ．‎ ‎17.如图，在 中， 是三角形外一点，且 ．求证： ____°．‎ 答案：60‎ 解析：首先延长 至 ，使 ，连接 ，由 ，易得 是等边三角形，继而证得 ，则可证得： ．‎ 证明：延长 至 ，使 ，连接，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ 是等边三角形，‎ ‎ ，‎ 在 和 中，‎ ‎ ，‎ ‎ ，‎ ‎ ．‎ ‎18.如图，凸六边形 的六个角都是 ，边长 ，求出这个六边形的周长为____ .‎ 答案：46‎ 解析：凸六边形，并不是一规则的六边形，但六个角都是 ，所以通过适当的向外作延长线，可得到等边三角形，进而求解．‎ 解：如图，分别作直线 的延长线使它们交于点 ．‎ 因为六边形的六个角都是，‎ 所以六边形的每一个外角的度数都是 ．‎ 所以三角形 、三角形 、三角形 、三角形 都是等边三角形．‎ 所以 ．‎ 所以 ， ， ．‎ 所以六边形的周长为 ．‎ ‎19.如图，在六边形中， ．‎ ‎（1）试说明 为等边三角形；‎ ‎（2）请探索 之间的关系（等量关系或位置关系）并说明理由．‎ 答案：见解析 解析：（1）根据多边形的内角和定理求出 ，求出 ，得出等边三角形 ，推出 ，同理求出 是等边三角形，推出 ，求出 ，即可求出答案．‎ 解：（1）作直线 、直线 、直线 和 交于 和 交于 和 交于 ，‎ ‎ ， ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ 为等边三角形．‎ ‎（2） ，‎ 理由是： ，‎ ‎ ，‎ ‎ ，‎ ‎ 是等边三角形，‎ ‎ ，‎ 同理 ，‎ ‎ ，‎ ‎ ，‎ ‎ 为等边三角形，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ， ，‎ ‎ ．‎ ‎20.如图所示，一个六边形的六个内角都是 ，其中连续四边的长依次是 ．求这个六边形的周长为____.‎ 答案：42‎ 解析：首先延长并反向延长 ，两两相交于点 ，可得 是等边三角形，同理： 是等边三角形，即可求得 与 ‎ 的长，继而求得答案.‎ 解：如图，延长并反向延长 ，两两相交于点，‎ ‎ 六边形 的每个内角都是，‎ ‎ ，‎ ‎ 是等边三角形，‎ 同理： 是等边三角形，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ ，‎ ‎ 六边形的周长 ．‎