2020九年级数学下册 第一章角的三角函数值 7页

课时作业(三)‎ ‎[第一章　2　30°，45 °，60°角的三角函数值]‎ 一、选择题 ‎1．2018·大庆2cos60°＝(　　)‎ A．1 B. C. D. ‎2．计算sin240°＋cos240°的值为(　　)‎ A．0 B. C．1 D．2‎ ‎3．在△ABC中，若∠C＝90°，tanA＝，则sinB的值为(　　)‎ A. B. C. D. ‎4．如图K－3－1，以点O为圆心，任意长为半径画弧，与射线OA交于点B，再以点B为圆心，BO长为半径画弧，两弧交于点C，画射线OC，则cos∠AOC的值为(　　)‎ 图K－3－1‎ A. B. C. D. 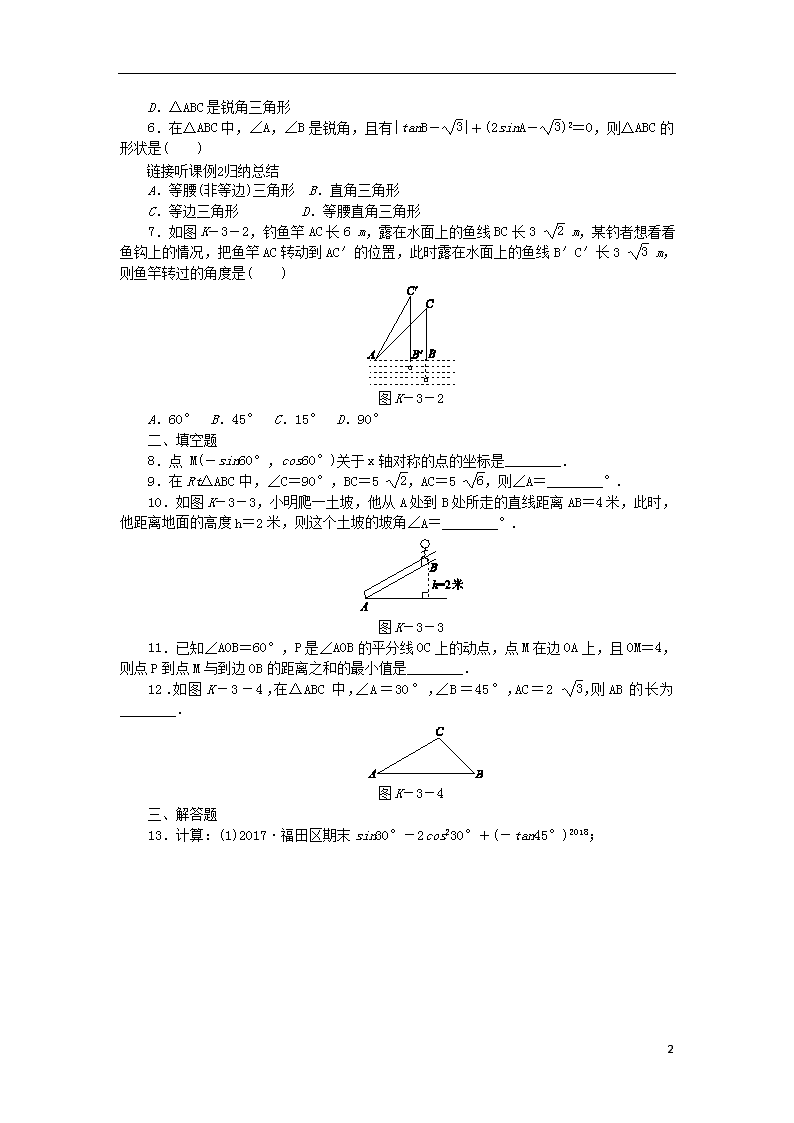‎5．如果在△ABC中，∠A，∠B为锐角，且sinA＝cosB＝，那么下列对△ABC最确切的描述是(　　)‎ A．△ABC是直角三角形 B．△ABC是等腰三角形 C．△ABC是等腰直角三角形 7‎ D．△ABC是锐角三角形 ‎6．在△ABC中，∠A，∠B是锐角，且有|tanB－|＋(2sinA－)2＝0，则△ABC的形状是(　　)‎ A．等腰(非等边)三角形 B．直角三角形 C．等边三角形 D．等腰直角三角形 ‎7．如图K－3－2，钓鱼竿AC长‎6 m，露在水面上的鱼线BC长‎3 ‎ m，某钓者想看看鱼钩上的情况，把鱼竿AC转动到AC′的位置，此时露在水面上的鱼线B′C′长‎3 ‎ m，则鱼竿转过的角度是(　　)‎ 图K－3－2‎ A．60° B．45° C．15° D．90°‎ 二、填空题 ‎8．点 M(－sin60°，cos60°)关于x轴对称的点的坐标是________．‎ ‎9．在Rt△ABC中，∠C＝90°，BC＝5 ，AC＝5 ，则∠A＝________°.‎ ‎10．如图K－3－3，小明爬一土坡，他从A处到B处所走的直线距离AB＝‎4米，此时，他距离地面的高度h＝‎2米，则这个土坡的坡角∠A＝________°.‎ 图K－3－3‎ ‎11．已知∠AOB＝60°，P是∠AOB的平分线OC上的动点，点M在边OA上，且OM＝4，则点P到点M与到边OB的距离之和的最小值是________．‎ ‎12．如图K－3－4，在△ABC中，∠A＝30°，∠B＝45°，AC＝2 ，则AB的长为________．‎ ‎　　‎ 图K－3－4‎ 三、解答题 ‎13．计算：(1)2017·福田区期末sin30°－2cos230°＋(－tan45°)2018；‎ 7‎ ‎(2)2017·上海普陀区一模cos245°＋－×tan30°.‎ ‎14．已知α为锐角，sin(α＋15°)＝，求－4cosα＋tanα＋()－1的值．‎ ‎15．如图K－3－5，一数学兴趣小组为测量河对岸树AB的高，在河岸边选择一点C，从C处测得树梢A的仰角为45°，沿BC方向后退‎10米到点D，再次测得点A的仰角为30°.求树高．(结果精确到‎0.1米，参考数据：≈1.414，≈1.732)‎ 图K－3－5‎ ‎16．如图K－3－6，矩形ABCD是供一辆机动车停放的车位示意图，已知BC＝‎2 m，CD＝‎5.4 m，∠DCF＝30°，请你计算车位所占的宽度EF为多少米．(≈1.73，结果精确到‎0.1 m)‎ 7‎ 图K－3－6‎ 新定义题对于钝角α，定义它的三角函数值如下：‎ sinα＝sin(180°－α)，cosα＝－cos(180°－α)．‎ ‎(1)求sin120°，cos120°，sin150°的值；‎ ‎(2)若一个三角形的三个内角的比是1∶1∶4，A，B是这个三角形的两个顶点，sinA，cosB是方程4x2－mx－1＝0的两个不相等的实数根，求m的值及∠A和∠B的度数．‎ 7‎ 详解详析 ‎【课时作业】‎ ‎[课堂达标]‎ ‎1．[解析] A　2cos60°＝2×＝1.‎ 故选A.‎ ‎2．[答案] C ‎3．[答案] C ‎4．[解析] A　连接BC，由题意可得：OB＝OC＝BC，则△OBC是等边三角形，故cos∠AOC＝cos60°＝.故选A.‎ ‎5．[解析] C　根据特殊角的三角函数值，直接得出∠A，∠B的度数．∵sinA＝cosB＝，∴∠A＝∠B＝45°，∴△ABC是等腰直角三角形．‎ ‎6．[解析] C　根据题意，得tanB－＝0，2sinA－＝0，∴tanB＝，sinA＝，∴∠B＝60°，∠A＝60°，故∠C＝60°，∴△ABC是等边三角形．故选C.‎ ‎7．[解析] C　∵sin∠CAB＝＝＝，∴∠CAB＝45°.∵sin∠C′AB′＝＝＝，∴∠C′AB′＝60°，∴∠CAC′＝60°－45°＝15°，即鱼竿转过的角度是15°.故选C.‎ ‎8．[答案] ‎[解析] ∵sin60°＝，cos60°＝，∴点M的坐标为.∵点M关于x轴对称的点，横坐标不变，纵坐标为其相反数，∴点M关于x轴对称的点的坐标是.‎ ‎9．[答案] 30　‎ ‎[解析] ∵在Rt△ABC中，∠C＝90°，BC＝5 ，AC＝5 ，∴tanA＝＝，∴∠A＝30°.故答案为30.‎ ‎10．[答案] 30‎ ‎11．[答案] 2 ‎[解析] 过点M作MN⊥OB，MN的长即为所求．‎ ‎∵∠AOB＝60°，OM＝4，‎ ‎∴MN＝4×sin60°＝2 .‎ ‎12．[答案] 3＋ ‎[解析] 过点C作CD⊥AB于点D，则△ACD和△BCD都是直角三角形．‎ 在Rt△ACD中，∠ADC＝90°，∠A＝30°，AC＝2 ，‎ ‎∴AD＝AC·cosA＝2 ×＝3，‎ 7‎ CD＝AC·sinA＝2 ×＝.‎ 在Rt△BCD中，∠BDC＝90°，‎ ‎∴BD＝CD＝，‎ ‎∴AB＝AD＋BD＝3＋.‎ ‎13．[解析] 根据特殊角的三角函数值，可得答案．‎ 解：(1)原式＝－2×()2＋(－1)2018＝－＋1＝0.‎ ‎(2)原式＝()2＋－×＝＋－1＝.‎ ‎14．解：∵sin(α＋15°)＝，α为锐角，‎ ‎∴α＝45°，‎ ‎∴－4cosα＋tanα＋()－1＝2 －2 ＋1＋3＝4.‎ ‎15．解：由题意，得∠B＝90°，∠D＝30°，∠ACB＝45°，DC＝‎10米，‎ 设AB＝x米，则CB＝x米，DB＝x米，‎ 所以x＝x＋10，所以(－1)x＝10，‎ 所以x＝＝5 ＋5≈5×1.732＋5＝8.66＋5＝13.66≈13.7.‎ 答：树高约为13.7米．‎ ‎16．解：在Rt△DCF中，‎ ‎∵CD＝5.4 m，∠DCF＝30°，sin∠DCF＝＝＝，‎ ‎∴DF＝2.7 m.‎ ‎∵∠CDF＋∠DCF＝90°，‎ ‎∠ADE＋∠CDF＝90°，‎ ‎∴∠ADE＝∠DCF＝30°.‎ ‎∵AD＝BC＝2 m，cos∠ADE＝＝＝，∴DE＝ m，‎ ‎∴EF＝DF＋DE≈2.7＋1.73≈4.4(m)．‎ 答：车位所占的宽度EF约为4.4 m.‎ ‎[素养提升]‎ ‎[解析] (1)按照题目所给的信息求解即可；‎ ‎(2)分三种情况进行分析：①当∠A＝30°，∠B＝120°时；②当∠A＝120°，∠B＝30°时；③当∠A＝30°，∠B＝30°时，根据题意分别求出m的值即可．‎ 解：(1)由题意得sin120°＝sin(180°－120°)＝sin60°＝，‎ cos120°＝－cos(180°－120°)＝－cos60°＝－，‎ sin150°＝sin(180°－150°)＝sin30°＝.‎ 7‎ ‎(2)∵三角形的三个内角的比是1∶1∶4，‎ ‎∴三角形的三个内角分别为30°，30°，120°.‎ ‎①当∠A＝30°，∠B＝120°时，方程的两根为，－.将代入方程，得4×()2－m×－1＝0，解得m＝0，即方程为4x2－1＝0.经检验，－是方程4x2－1＝0的根，∴∠A＝30°，∠B＝120°符合题意；‎ ‎②当∠A＝120°，∠B＝30°时，方程的两根为，，不符合题意；‎ ‎③当∠A＝30°，∠B＝30°时，方程的两根为，，将代入方程，得4×()2－m×－1＝0，解得m＝0，即方程为4x2－1＝0.‎ 经检验，不是方程4x2－1＝0的根，‎ ‎∴∠A＝30°，∠B＝30°不符合题意．‎ 综上所述，m＝0，∠A＝30°，∠B＝120°.‎ 7‎