2020年江苏省淮安市中考数学试卷【含答案】 12页

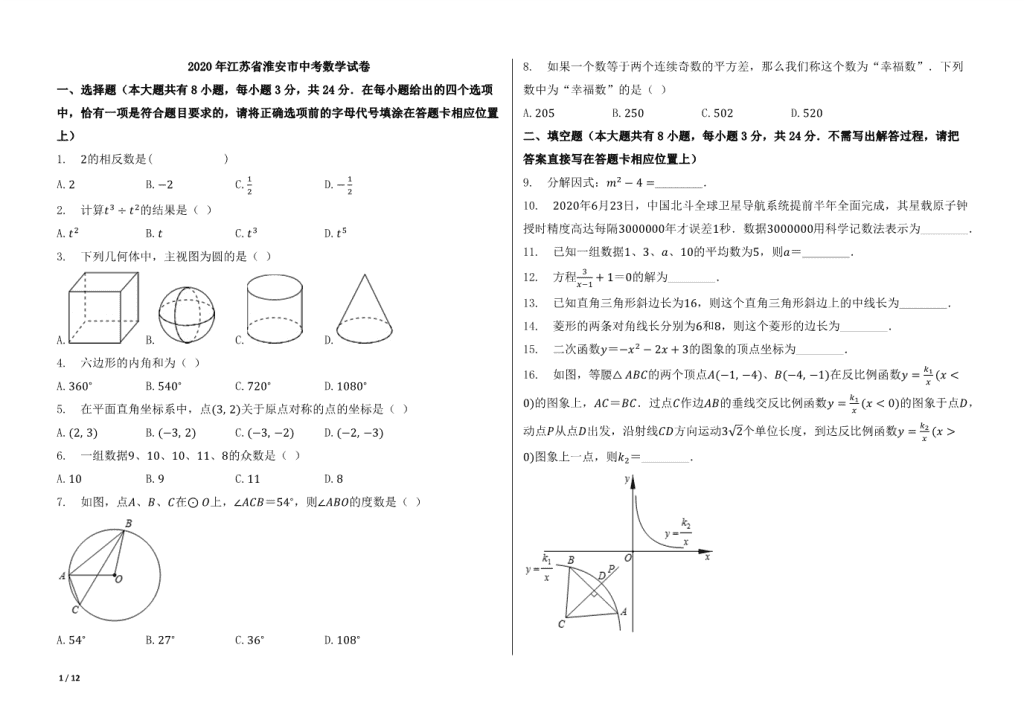
1 / 12 2020 年江苏省淮安市中考数学试卷 一、选择题（本大题共有 8 小题，每小题 3 分，共 24 分．在每小题给出的四个选项 中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置 上） 1. 2的相反数是( ) A.2 B.−2 C.1 2 D.− 1 2 2. 计算푡3 ÷ 푡2的结果是（ ） A.푡2 B.푡 C.푡3 D.푡5 3. 下列几何体中，主视图为圆的是（ ） A. B. C. D. 4. 六边形的内角和为（ ） A.360∘ B.540∘ C.720∘ D.1080∘ 5. 在平面直角坐标系中，点(3,  2)关于原点对称的点的坐标是（ ） A.(2,  3) B.(−3,  2) C.(−3, −2) D.(−2, −3) 6. 一组数据9、10、10、11、8的众数是（ ） A.10 B.9 C.11 D.8 7. 如图，点퐴、퐵、퐶在⊙ 푂上，∠퐴퐶퐵＝54∘，则∠퐴퐵푂的度数是（ ） A.54∘ B.27∘ C.36∘ D.108∘ 8. 如果一个数等于两个连续奇数的平方差，那么我们称这个数为“幸福数”．下列 数中为“幸福数”的是（ ） A.205 B.250 C.502 D.520 二、填空题（本大题共有 8 小题，每小题 3 分，共 24 分．不需写出解答过程，请把 答案直接写在答题卡相应位置上） 9. 分解因式：푚2 − 4 =________． 10. 2020年6月23日，中国北斗全球卫星导航系统提前半年全面完成，其星载原子钟 授时精度高达每隔3000000年才误差1秒．数据3000000用科学记数法表示为________． 11. 已知一组数据1、3、푎、10的平均数为5，则푎＝________． 12. 方程 3 푥−1 + 1＝0的解为________． 13. 已知直角三角形斜边长为16，则这个直角三角形斜边上的中线长为________． 14. 菱形的两条对角线长分别为6和8，则这个菱形的边长为________． 15. 二次函数푦＝−푥2 − 2푥 + 3的图象的顶点坐标为________． 16. 如图，等腰△ 퐴퐵퐶的两个顶点퐴(−1, −4)、퐵(−4, −1)在反比例函数푦 = 푘1 푥 (푥 < 0)的图象上，퐴퐶＝퐵퐶．过点퐶作边퐴퐵的垂线交反比例函数푦 = 푘1 푥 (푥 < 0)的图象于点퐷， 动点푃从点퐷出发，沿射线퐶퐷方向运动3√2个单位长度，到达反比例函数푦 = 푘2 푥 (푥 > 0)图象上一点，则푘2＝________． 2 / 12 三、解答题（本大题共有 11 小题，共 102 分．请在答题卡指定区域内作答，解答时 应写出必要的文字说明、证明过程或演算步骤） 17. 计算： （1）| − 3| + (휋 − 1)0 − √4； （2）푥+1 2푥 ÷ (1 + 1 푥)． 18. 解不等式2푥 − 1 > 3푥−1 2 ． 解：去分母，得2(2푥 − 1) > 3푥 − 1． … （1）请完成上述解不等式的余下步骤： （2）解题回顾：本题“去分母”这一步的变形依据是________（填“퐴”或“퐵”）． 퐴．不等式两边都乘（或除以）同一个正数，不等号的方向不变； 퐵．不等式两边都乘（或除以）同一个负数，不等号的方向改变． 19. 某停车场的收费标准如下：中型汽车的停车费为15元/辆，小型汽车的停车费为 8元/辆．现在停车场内停有30辆中、小型汽车，这些车共缴纳停车费324元，求中、 小型汽车各有多少辆？ 20. 如图，在▱퐴퐵퐶퐷中，点퐸、퐹分别在퐵퐶、퐴퐷上，퐴퐶与퐸퐹相交于点푂，且퐴푂＝ 퐶푂． 3 / 12 （1）求证：△ 퐴푂퐹 ≅△ 퐶푂퐸； （2）连接퐴퐸、퐶퐹，则四边形퐴퐸퐶퐹 是 （填“是”或“不是”）平行四边形． 21. 为了响应市政府创建文明城市的号召，某校调查学生对市“文明公约十二条”的 内容了解情况，随机抽取部分学生进行问卷调查，问卷共设置“非常了解”、“比较 了解”、“一般了解”、“不了解”四个选项，分别记为퐴、퐵、퐶、퐷，根据调查结 果绘制了如图尚不完整的统计图． 请解答下列问题： （1）本次问卷共随机调查了________学生，扇形统计图中퐶选项对应的圆心角为 ________度； （2）请补全条形统计图； （3）若该校有1200名学生，试估计该校选择“不了解”的学生有多少人？ 22. 一只不透明的袋子中，装有三个大小、质地都相同的乒乓球，球面上分别标有字 母퐴、푂、퐾．搅匀后先从袋中任意摸出一个球，将对应字母记入图中的左边方格内； 然后将球放回袋中搅匀，再从袋中任意摸出一个球，将对应字母记入图中的右边方格 内． 4 / 12 （1）第一次摸到字母퐴的概率为________； （2）用画树状图或列表等方法求两个方格中的字母从左往右恰好组成“푂퐾”的概率． 23. 如图，三条笔直公路两两相交，交点分别为퐴、퐵、퐶，测得∠퐶퐴퐵＝30∘，∠퐴퐵퐶 ＝45∘，퐴퐶＝8千米，求퐴、퐵两点间的距离．（参考数据：√2 ≈ 1.4，√3 ≈ 1.7，结果 精确到1千米）． 24. 甲、乙两地的路程为290千米，一辆汽车早上8: 00从甲地出发，匀速向乙地行驶， 途中休息一段时间后．按原速继续前进，当离甲地路程为240千米时接到通知，要求 中午12: 00准时到达乙地．设汽车出发푥小时后离甲地的路程为푦千米，图中折线 푂퐶퐷퐸表示接到通知前푦与푥之间的函数关系． 5 / 12 （1）根据图象可知，休息前汽车行驶的速度为________千米/小时； （2）求线段퐷퐸所表示的푦与푥之间的函数表达式； （3）接到通知后，汽车仍按原速行驶能否准时到达？请说明理由． 25. 如图，퐴퐵是⊙ 푂的弦，퐶是⊙ 푂外一点，푂퐶 ⊥ 푂퐴，퐶푂交퐴퐵于点푃，交⊙ 푂于点 퐷，且퐶푃＝퐶퐵． （1）判断直线퐵퐶与⊙ 푂的位置关系，并说明理由； （2）若∠퐴＝30∘，푂푃＝1，求图中阴影部分的面积． 26. [初步尝试] （1）如图①，在三角形纸片퐴퐵퐶中，∠퐴퐶퐵＝90∘，将△ 퐴퐵퐶折叠，使点퐵与点퐶重合， 折痕为푀푁，则퐴푀与퐵푀的数量关系为________； [思考说理] （2）如图②，在三角形纸片퐴퐵퐶中，퐴퐶＝퐵퐶＝6，퐴퐵＝10，将△ 퐴퐵퐶折叠，使点퐵 与点퐶重合，折痕为푀푁，求퐴푀 퐵푀 的值； 6 / 12 [拓展延伸] （3）如图③，在三角形纸片퐴퐵퐶中，퐴퐵＝9，퐵퐶＝6，∠퐴퐶퐵＝2∠퐴，将△ 퐴퐵퐶沿过 顶点퐶的直线折叠，使点퐵落在边퐴퐶上的点퐵′处，折痕为퐶푀． ①求线段퐴퐶的长； ②若点푂是边퐴퐶的中点，点푃为线段푂퐵′上的一个动点，将△ 퐴푃푀沿푃푀折叠得到△ 퐴′푃푀，点퐴的对应点为点퐴′，퐴′푀与퐶푃交于点퐹，求푃퐹 푀퐹 的取值范围． 27. 如图①，二次函数푦＝−푥2 + 푏푥 + 4的图象与直线푙交于퐴(−1,  2)、퐵(3,  푛)两 点．点푃是푥轴上的一个动点，过点푃作푥轴的垂线交直线1于点푀，交该二次函数的图 象于点푁，设点푃的横坐标为푚． （1）푏＝________，푛＝________； （2）若点푁在点푀的上方，且푀푁＝3，求푚的值； （3）将直线퐴퐵向上平移4个单位长度，分别与푥轴、푦轴交于点퐶、퐷（如图②）． ①记△ 푁퐵퐶的面积为푆1，△ 푁퐴퐶的面积为푆2，是否存在푚，使得点푁在直线퐴퐶的上方， 且满足푆1 − 푆2＝6？若存在，求出푚及相应的푆1，푆2的值；若不存在，请说明理由． ②当푚 > −1时，将线段푀퐴绕点푀顺时针旋转90∘得到线段푀퐹，连接퐹퐵、퐹퐶、 푂퐴．若∠퐹퐵퐴 + ∠퐴푂퐷 − ∠퐵퐹퐶＝45∘，直接写出直线푂퐹与该二次函数图象交点的横坐 标． 7 / 12 参考答案与试题解析 2020 年江苏省淮安市中考数学试卷 一、选择题（本大题共有 8 小题，每小题 3 分，共 24 分．在每小题给出的四个选项 中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置 上） 1.B 2.B 3.B 4.C 5.C 6.A 7.C 8.D 二、填空题（本大题共有 8 小题，每小题 3 分，共 24 分．不需写出解答过程，请把 答案直接写在答题卡相应位置上） 9.(푚 + 2)(푚 − 2) 10.3 × 106 11.6 12.푥＝−2 13.8 14.5 15.(−1,  4) 16.1 三、解答题（本大题共有 11 小题，共 102 分．请在答题卡指定区域内作答，解答时 应写出必要的文字说明、证明过程或演算步骤） 17.| − 3| + (휋 − 1)0 − √4 ＝3 + 1 − 2 ＝2； 푥 + 1 2푥 ÷ (1 + 1 푥) = 푥 + 1 2푥 ÷ 푥 + 1 푥 = 푥 + 1 2푥 ⋅ 푥 푥 + 1 = 1 2 ． 18.去分母，得：4푥 − 2 > 3푥 − 1， 移项，得：4푥 − 3푥 > 2 − 1， 合并同类项，得：푥 > 1， 퐴 19.中型汽车有12辆，小型汽车有18辆 20.证明：∵ 四边形퐴퐵퐶퐷是平行四边形， ∴ 퐴퐷 // 퐵퐶， ∴ ∠푂퐴퐹＝∠푂퐶퐸， 在△ 퐴푂퐹和△ 퐶푂퐸中，{ ∠푂퐴퐹 = ∠푂퐶퐸 퐴푂 = 퐶푂 ∠퐴푂퐹 = ∠퐶푂퐸 ， ∴ △ 퐴푂퐹 ≅△ 퐶푂퐸(퐴푆퐴) 四边形퐴퐸퐶퐹是平行四边形，理由如下： 由（1）得：△ 퐴푂퐹 ≅△ 퐶푂퐸， ∴ 퐹푂＝퐸푂， 又∵ 퐴푂＝퐶푂， 8 / 12 ∴ 四边形퐴퐸퐶퐹是平行四边形； 故答案为：是． 21.60名,108 该校1200名学生中选择“不了解”的有60人 22.1 3 用树状图表示所有可能出现的结果如下： 共有9种可能出现的结果，其中从左到右能构成“푂퐾”的只有1种， ∴ 푃（组成푂퐾） = 1 9 ． 23.퐴、퐵两点间的距离约为11千米． 24.80 休息后按原速继续前进行驶的时间为：(240 − 80) ÷ 80＝2（小时）， ∴ 点퐸的坐标为(3.5,  240)， 设线段퐷퐸所表示的푦与푥之间的函数表达式为푦＝푘푥 + 푏，则： { 1.5푘 + 푏 = 80 3.5푘 + 푏 = 240 ，解得{ 푘 = 80 푏 = −40 ， ∴ 线段퐷퐸所表示的푦与푥之间的函数表达式为：푦＝80푥 − 40； 接到通知后，汽车仍按原速行驶，则全程所需时间为：290 ÷ 80 + 0.5＝4.125（小时）， 12: 00 − 8: 00＝4（小时）， 4.125 > 4， 所以接到通知后，汽车仍按原速行驶不能准时到达． 25.퐶퐵与⊙ 푂相切， 理由：连接푂퐵， ∵ 푂퐴＝푂퐵， ∴ ∠푂퐴퐵＝∠푂퐵퐴， ∵ 퐶푃＝퐶퐵， ∴ ∠퐶푃퐵＝∠퐶퐵푃， 在푅푡 △ 퐴푂푃中，∵ ∠퐴 + ∠퐴푃푂＝90∘， ∴ ∠푂퐵퐴 + ∠퐶퐵푃＝90∘， 即：∠푂퐵퐶＝90∘， 9 / 12 ∴ 푂퐵 ⊥ 퐶퐵， 又∵ 푂퐵是半径， ∴ 퐶퐵与⊙ 푂相切； ∵ ∠퐴＝30∘，∠퐴푂푃＝90∘， ∴ ∠퐴푃푂＝60∘， ∴ ∠퐵푃퐷＝∠퐴푃푂＝60∘， ∵ 푃퐶＝퐶퐵， ∴ △ 푃퐵퐶是等边三角形， ∴ ∠푃퐶퐵＝∠퐶퐵푃＝60∘， ∴ ∠푂퐵푃＝∠푃푂퐵＝30∘， ∴ 푂푃＝푃퐵＝푃퐶＝1， ∴ 퐵퐶＝1， ∴ 푂퐵 = √푂퐶2 − 퐵퐶2 = √3， ∴ 图中阴影部分的面积＝푆△푂퐵퐶 − 푆扇形푂퐵퐷 = 1 2 × 1 × √3 − 30⋅휋×(√3)2 360 = √3 2 − 휋 4 ． 26.퐴푀＝퐵푀 如图②中， ∵ 퐶퐴＝퐶퐵＝6， ∴ ∠퐴＝∠퐵， 由题意푀푁垂直平分线段퐵퐶， ∴ 퐵푀＝퐶푀， ∴ ∠퐵＝∠푀퐶퐵， ∴ ∠퐵퐶푀＝∠퐴， ∵ ∠퐵＝∠퐵， ∴ △ 퐵퐶푀 ∽△ 퐵퐴퐶， ∴ 퐵퐶 퐵퐴 = 퐵푀 퐵퐶 ， ∴ 6 10 = 퐵푀 6 ， ∴ 퐵푀 = 18 5 ， ∴ 퐴푀＝퐴퐵 − 퐵푀＝10 − 18 5 = 32 5 ， ∴ 퐴푀 퐵푀 = 32 5 18 5 = 16 9 ． ①如图③中， 由折叠的性质可知，퐶퐵＝퐶퐵′＝6，∠퐵퐶푀＝∠퐴퐶푀， 10 / 12 ∵ ∠퐴퐶퐵＝2∠퐴， ∴ ∠퐵퐶푀＝∠퐴， ∵ ∠퐵＝∠퐵， ∴ △ 퐵퐶푀 ∽△ 퐵퐴퐶， ∴ 퐵퐶 퐴퐵 = 퐵푀 퐵퐶 = 퐶푀 퐴퐶 ∴ 6 9 = 퐵푀 6 ， ∴ 퐵푀＝4， ∴ 퐴푀＝퐶푀＝5， ∴ 6 9 = 5 퐴퐶 ， ∴ 퐴퐶 = 15 2 ． ②如图③−1中， ∵ ∠퐴＝∠퐴′＝∠푀퐶퐹，∠푃퐹퐴′＝∠푀퐹퐶，푃퐴＝푃퐴′， ∴ △ 푃퐹퐴′ ∽△ 푀퐹퐶， ∴ 푃퐹 퐹푀 = 푃퐴′ 퐶푀 ， ∵ 퐶푀＝5， ∴ 푃퐹 퐹푀 = 푃퐴′ 5 ， ∵ 点푃在线段푂퐵上运动，푂퐴＝푂퐶 = 15 4 ，퐴퐵′ = 15 2 − 6 = 3 2 ， ∴ 3 2 ≤ 푃퐴′ ≤ 15 4 ， ∴ 3 10 ≤ 푃퐹 퐹푀 ≤ 3 4 ． 27.1,−2 知，点퐵(3, −2)， ∵ 퐴(−1,  2)， ∴ { −푘 + 푎 = 2 3푘 + 푎 = −2 ， ∴ {푘 = −1 푎 = 1 ， ∴ 直线퐴퐵的解析式为푦＝−푥 + 1， 由 知，二次函数的解析式为푦＝−푥2 + 푥 + 4， ∵ 点푃(푚,  0)， ∴ 푀(푚, −푚 + 1)，푁(푚, −푚2 + 푚 + 4)， ∵ 点푁在点푀的上方，且푀푁＝3， ∴ −푚2 + 푚 + 4 − (−푚 + 1)＝3， ∴ 푚＝0或푚＝2； （1）①如图1，由（2）知，直线퐴퐵的解析式为푦＝−푥 + 1， ∴ 直线퐶퐷的解析式为푦＝−푥 + 1 + 4＝−푥 + 5， 令푦＝0，则−푥 + 5＝0， ∴ 푥＝5， ∴ 퐶(5,  0)， ∵ 퐴(−1,  2)，퐵(3, −2)， ∴ 直线퐴퐶的解析式为푦 = − 1 3 푥 + 5 3 ，直线퐵퐶的解析式为푦＝푥 − 5， 过点푁作푦轴的平行线交퐴퐶于퐾，交퐵퐶于퐻，∵ 点푃(푚,  0)， ∴ 푁(푚, −푚2 + 푚 + 4)，퐾(푚, − 1 3 푚 + 5 3)，퐻(푚,  푚 − 5)， 11 / 12 ∴ 푁퐾＝−푚2 + 푚 + 4 + 1 3 푚 − 5 3 = −푚2 + 4 3 푚 + 7 3 ，푁퐻＝−푚2 + 9， ∴ 푆2＝푆△푁퐴퐶 = 1 2 푁퐾 × (푥퐶 − 푥퐴) = 1 2 (−푚2 + 4 3 푚 + 7 3) × 6＝−3푚2 + 4푚 + 7， 푆1＝푆△푁퐵퐶 = 1 2 푁퐻 × (푥퐶 − 푥퐵)＝−푚2 + 9， ∵ 푆1 − 푆2＝6， ∴ −푚2 + 9 − (−3푚2 + 4푚 + 7)＝6， ∴ 푚＝1 + √3（由于点푁在直线퐴퐶上方，所以，舍去）或푚＝1 − √3； ∴ 푆2＝−3푚2 + 4푚 + 7＝−3(1 − √3)2 + 4(1 − √3) + 7＝2√3 − 1， 푆1＝−푚2 + 9＝−(1 − √3)2 + 9＝2√3 + 5； ②如图2， 记直线퐴퐵与푥轴，푦轴的交点为퐼，퐿， 由（3）知，直线퐴퐵的解析式为푦＝−푥 + 1， ∴ 퐼(1,  0)，퐿(0,  1)， ∴ 푂퐿＝푂퐼， ∴ ∠퐴퐿퐷＝∠푂퐿퐼＝45∘， ∴ ∠퐴푂퐷 + ∠푂퐴퐵＝45∘， 过点퐵作퐵퐺 // 푂퐴， ∴ ∠퐴퐵퐺＝∠푂퐴퐵， ∴ ∠퐴푂퐷 + ∠퐴퐵퐺＝45∘， ∵ ∠퐹퐵퐴＝∠퐴퐵퐺 + ∠퐹퐵퐺，∠퐹퐵퐴 + ∠퐴푂퐷 − ∠퐵퐹퐶＝45∘， ∴ ∠퐴퐵퐺 + ∠퐹퐵퐺 + ∠퐴푂퐷 − ∠퐵퐹퐶＝45∘， ∴ ∠퐹퐵퐺＝∠퐵퐹퐶， ∴ 퐵퐺 // 퐶퐹， ∴ 푂퐴 // 퐶퐹， ∵ 퐴(−1,  2)， ∴ 直线푂퐴的解析式为푦＝−2푥， ∵ 퐶(5,  0)， ∴ 直线퐶퐹的解析式为푦＝−2푥 + 10， 过点퐴，퐹分别作过点푀平行于푥轴的直线的垂线，交于点푄，푆， ∵ ∠퐴푄푀＝∠푀푆퐹＝90∘， ∵ 点푀在直线퐴퐵上，푚 > −1， ∴ 푀(푚, −푚 + 1)， ∴ 퐴(−1,  2)， ∴ 푀푄＝푚 + 1， 设点퐹(푛, −2푛 + 10)， ∴ 퐹푆＝−2푛 + 10 + 푚 − 1＝−2푛 + 푚 + 9， 由旋转知，퐴푀＝푀퐹，∠퐴푀퐹＝90∘， ∴ ∠푀퐴푄 + ∠퐴푀푄＝90∘＝∠퐴푀푄 + ∠퐹푀푆， ∴ ∠푀퐴푄＝∠퐹푀푆， ∴ △ 퐴푄푀 ≅△ 푀푆퐹(퐴퐴푆)， ∴ 퐹푆＝푀푄， ∴ −2푛 + 푚 + 9＝푚 + 1， ∴ 푛＝4， ∴ 퐹(4,  2)， ∴ 直线푂퐹的解析式为푦 = 1 2 푥①， ∵ 二次函数的解析式为푦＝−푥2 + 푥 + 4②， 联立①②解得，{ 푥 = 1+√65 4 푦 = 1+√65 8 或{ 푥 = 1−√65 4 푦 = 1−√65 8 ， ∴ 直线푂퐹与该二次函数图象交点的横坐标为1+√65 4 或1−√65 4 ． 12 / 12