2020年秋九年级数学上册 第3章圆的基本性质 9页

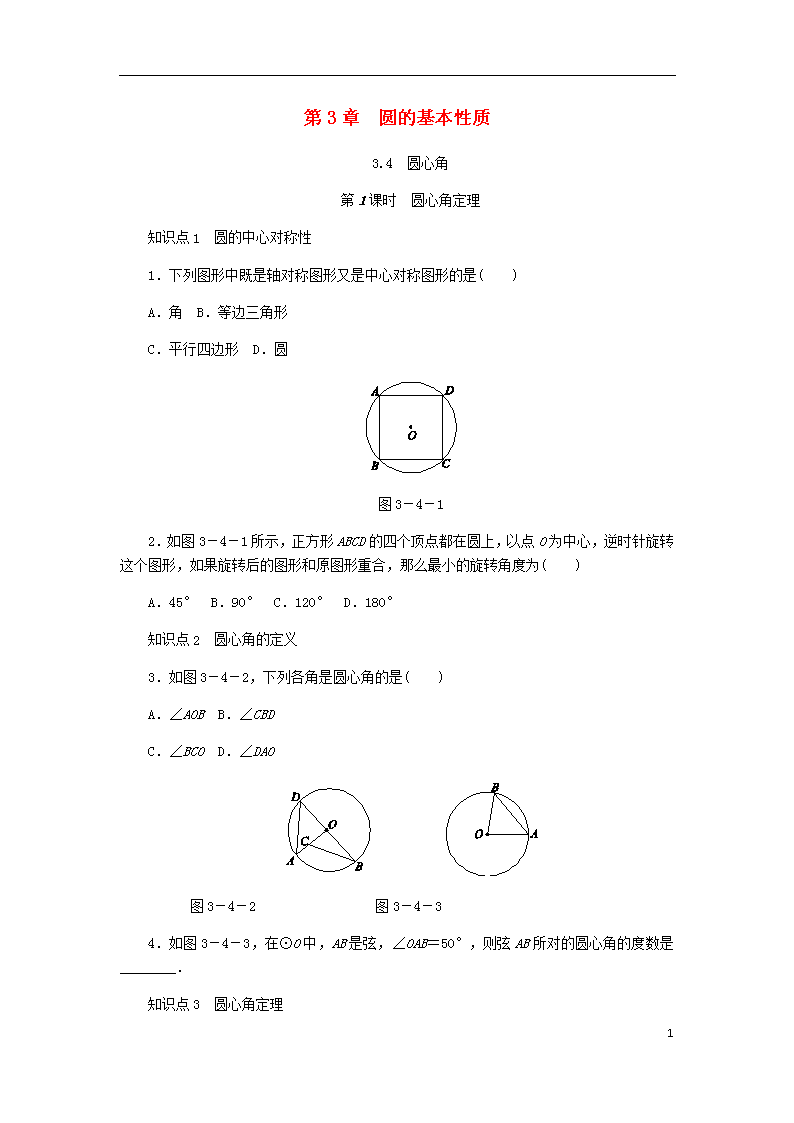
第3章　圆的基本性质 ‎3.4　圆心角 第1课时　圆心角定理 知识点1　圆的中心对称性 ‎1．下列图形中既是轴对称图形又是中心对称图形的是(　　)‎ A．角 B．等边三角形 C．平行四边形 D．圆 图3－4－1‎ ‎2．如图3－4－1所示，正方形ABCD的四个顶点都在圆上，以点O为中心，逆时针旋转这个图形，如果旋转后的图形和原图形重合，那么最小的旋转角度为(　　)‎ A．45° B．90° C．120° D．180°‎ 知识点2　圆心角的定义 ‎3．如图3－4－2，下列各角是圆心角的是(　　)‎ A．∠AOB B．∠CBD C．∠BCO D．∠DAO ‎　　　图3－4－2　　　　　 　　　图3－4－3‎ ‎4．如图3－4－3，在⊙O中，AB是弦，∠OAB＝50°，则弦AB所对的圆心角的度数是________．‎ 知识点3　圆心角定理 9‎ ‎5．下列命题是真命题的是(　　)‎ A．相等的圆心角所对的弧相等 B．相等的圆心角所对的弦相等 C．在同圆中，相等的圆心角所对的弧相等 D．顶点在圆内的角是圆心角 图3－4－4‎ ‎6．如图3－4－4，AB是⊙O的直径，∠BOC＝∠COD＝∠DOE＝36°，则下列说法错误的是(　　)‎ A．C是的中点 B．D是的中点 C．E是的中点 D．E是的中点 ‎7．已知：如图3－4－5，在⊙O中，∠AOD＝∠BOC.求证：AB＝CD.‎ 图3－4－5‎ 9‎ ‎8．如图3－4－6，D，E分别是⊙O的半径OA，OB上的点，且CD⊥OA，CE⊥OB，CD＝CE，求证：C是的中点．‎ 图3－4－6‎ 知识点4　圆心角度数与它所对的弧的度数的关系 ‎9．如图3－4－7所示，点A，B，C在⊙O上，OA∥BC，∠OBC＝40°，则的度数是(　　)‎ A．10° B．20° C．40° D．70°‎ 图3－4－7‎ ‎　　图3－4－8‎ 9‎ ‎10．如图3－4－8，若∠AOB＝100°，则的度数为________．‎ ‎11．下列圆的内接正多边形中，一条边所对的圆心角最大的图形是(　　)‎ A．正三角形 B．正方形 C．正五边形 D．正六边形 ‎12．在半径为2的⊙O内有长为2 的弦AB，则此弦所对的圆心角∠AOB为(　　)‎ A．60° B．90° C．120° D．150°‎ ‎13．2016·舟山把一张圆形纸片按如图3－4－9所示方式折叠两次后展开，图中的虚线表示折痕，则的度数是(　　)‎ 图3－4－9‎ A．120° B．135° C．150° D．165°‎ 图3－4－10‎ ‎14．2016·义乌期中如图3－4－10，在半径为5的⊙A中，弦BC，ED所对的圆心角分别是∠BAC，∠EAD.已知DE＝6，∠BAC＋∠EAD＝180°，则圆心A到弦BC的距离为________．‎ ‎15．如图3－4－11，以Rt△ABC的直角顶点为圆心，以BA为半径的圆分别交AC于点D，交BC于点E.若∠C＝31°，求的度数．‎ 9‎ 图3－4－11‎ ‎16．如图3－4－12，△ABC是等边三角形，以BC为直径画⊙O分别交AB，AC于点D，E.求证：BD＝CE.‎ 图3－4－12‎ ‎17．(1)如图3－4－13，M，N分别是⊙O的内接正三角形ABC的边AB，BC上的点，且BM＝CN，连结OM，ON，求∠MON的度数；‎ ‎(2)若M，N分别是⊙O的内接正方形ABCD的边AB，BC上的点，且BM＝CN，连结OM，ON，则∠MON的度数是________；‎ 9‎ ‎(3)若M，N分别是⊙O的内接正五边形ABCDE的边AB，BC上的点，且BM＝CN，连结OM，ON，则∠MON的度数是________；‎ ‎(4)若M，N分别是⊙O的内接正n边形ABCDE…的边AB，BC上的点，且BM＝CN，连结OM，ON，则∠MON的度数是________．‎ 图3－4－13‎ 9‎ 详解详析 ‎1．D　2.B　3.A ‎4．80°‎ ‎5．C　[解析] 叙述圆心角的性质时，必须加上“在同圆或等圆中”．‎ ‎6．C　[解析] ∵∠BOC＝∠COD＝∠DOE＝36°，∴∠AOE＝180°－3×36°＝72°，∠COE＝2×36°＝72°，∴∠AOE＝∠COE，∴＝＝，＝，∴C是的中点，D是的中点，E是的中点，故选C.‎ ‎7．证明：法一：∵∠AOD＝∠BOC，‎ ‎∴∠AOB＝∠COD.‎ 又∵OA＝OC，OB＝OD，‎ ‎∴△AOB≌△COD，‎ ‎∴AB＝CD.‎ 法二：∵∠AOD＝∠BOC，‎ ‎∴∠AOB＝∠COD，∴AB＝CD.‎ ‎8．证明：∵CD⊥OA，CE⊥OB，‎ ‎∴∠CDO＝∠CEO＝90°.‎ 又∵CD＝CE，CO＝CO，‎ ‎∴Rt△COD≌Rt△COE，‎ ‎∴∠AOC＝∠BOC，‎ ‎∴＝，‎ 即C是的中点．‎ ‎9．C　[解析] ∵OA∥BC，∴∠AOB＝∠OBC＝40°，故的度数是40°.‎ 9‎ ‎10．260°‎ ‎11．A　[解析] 正三角形的边所对的圆心角是120°；正方形的边所对的圆心角是90°；正五边形的边所对的圆心角是72°；正六边形的边所对的圆心角是60°.故选A.‎ ‎12．C ‎13．C　[解析] 如图所示，连结BO，过点O作OE⊥AB于点E.由题意可得EO＝BO，AB∥DC，可得∠EBO＝30°，故∠BOD＝30°，则∠BOC＝150°，故的度数是150°.‎ ‎14．3　[解析] 如图，过点A作AH⊥BC于点H，作直径CF，连结BF.‎ ‎∵∠BAC＋∠EAD＝180°，‎ 而∠BAC＋∠BAF＝180°，∴∠DAE＝∠BAF，∴＝，∴DE＝BF＝6.‎ ‎∵AH⊥BC，∴CH＝BH.∵CA＝AF，‎ ‎∴AH为△CBF的中位线，∴AH＝BF＝3，‎ ‎∴点A到弦BC的距离为3.‎ ‎15．连结BD.‎ 在Rt△ABC中，∠ABC＝90°，∠C＝31°，‎ ‎∴∠A＝90°－∠C＝59°.‎ 又BA＝BD，∴∠BDA＝∠A＝59°，‎ ‎∴∠ABD＝180°－∠BDA－∠A＝62°，‎ 9‎ ‎∴的度数为62°.‎ ‎16．证明：如图，连结OD，OE.‎ ‎∵△ABC是等边三角形，‎ ‎∴∠B＝∠C＝60°.‎ 又∵OB＝OD，OE＝OC，‎ ‎∴△BOD，△OEC都是等边三角形，‎ ‎∴∠BOD＝∠COE＝60°，∴BD＝CE.‎ ‎17．解：(1)连结OB，OC.‎ ‎∵正三角形ABC内接于⊙O，‎ ‎∴∠OBA＝∠OBC＝∠ABC＝×60°＝30°，‎ 同理，∠OCB＝∠OCA＝∠ACB＝×60°＝30°，‎ ‎∴∠OBA＝∠OCB.∵OB＝OC，BM＝CN，‎ ‎∴△OBM≌△OCN，∴∠BOM＝∠CON，‎ ‎∴∠MON＝∠BOM＋∠BON＝∠CON＋∠BON＝∠BOC.易知＝＝，‎ ‎∴的度数为×360°＝120°，‎ ‎∴∠MON＝∠BOC＝120°.‎ ‎(2)90°　(3)72°　(4) 9‎