2014中考数学模拟试卷含答案(上海一模)虹口 7页

上海市虹口区 2014 年中考一模（即期末） 数学试题（2014 年 1 月） （考试时间：100 分钟，满分：150 分） 一、 选择题（本大题共 6 题，每题 4 分，满分 24 分） 1．下列函数中属于二次函数的是（ ▲ ） A． 2y x ； B． 2( 1)( 3)y x x   ； C． 32yx； D． 2 1xy x  ． 2．抛物线 2 32y x x   与 y 轴交点的坐标是（ ▲ ） A． 51 2 AC BC  ； B． 51 2 AC AB  ； C． 51 2 BC AB  ； D． 51 2 CB AC  ． 3．在 Rt△ABC 中，∠ C=90°，若 a、b、c 分别∠A、∠B、∠C 的对边，则下列结论中，正确的是（ ▲ ） A． sinc A a； B． cosb B c； C． tana A b； D． tanc B b． 4．如图，若 AB // CD // EF，则下列结论中，与 AD AF 相等的是（ ▲ ） A． AB EF ； B． CD EF ； C． BO OE ； D． BC BE ． 5．如图，在△ABC 中，如果 DE 与 BC 不平行，那么下列条件中，不能判断△ADE∽△ABC 的是（ ▲ ） A．∠ADE =∠C； B．∠AED =∠B； C． AD DE AB BC ； D． AD AE AC AB ． 6．如图，在四边形 ABCD 中，点 E、F 分别是 AB、AD 的中点，若 EF = 2，BC = 5，CD = 3，则 sinC 的值为（ ▲ ） A． 3 4 ； B． 4 3 ； C． 3 5 ； D． 4 5 ． 二、填空题（本大题共 12 题，每题 4 分，满分 48 分） 7．已知 : 3: 2xy ，则( ):xyx ▲ ． 8．计算： 22 cos45 sin 60   ▲ ． 9．在 Rt△ABC 中，∠C = 90°，若 AC=5，tanA = 2，则 BC= ▲ ． 10．写出抛物线 21 2yx 与抛物线 21 2yx 的一条共同特征是 ▲ ． 11．已知抛物线 22( 3) 1yx    ，当 123xx时， 12____yy．（填“>”或“<”） 12．将抛物线 23yx 平移，使其顶点移到点 P（– 2 , 1）的位置，则所得新抛物线的表达式是 ▲ ． 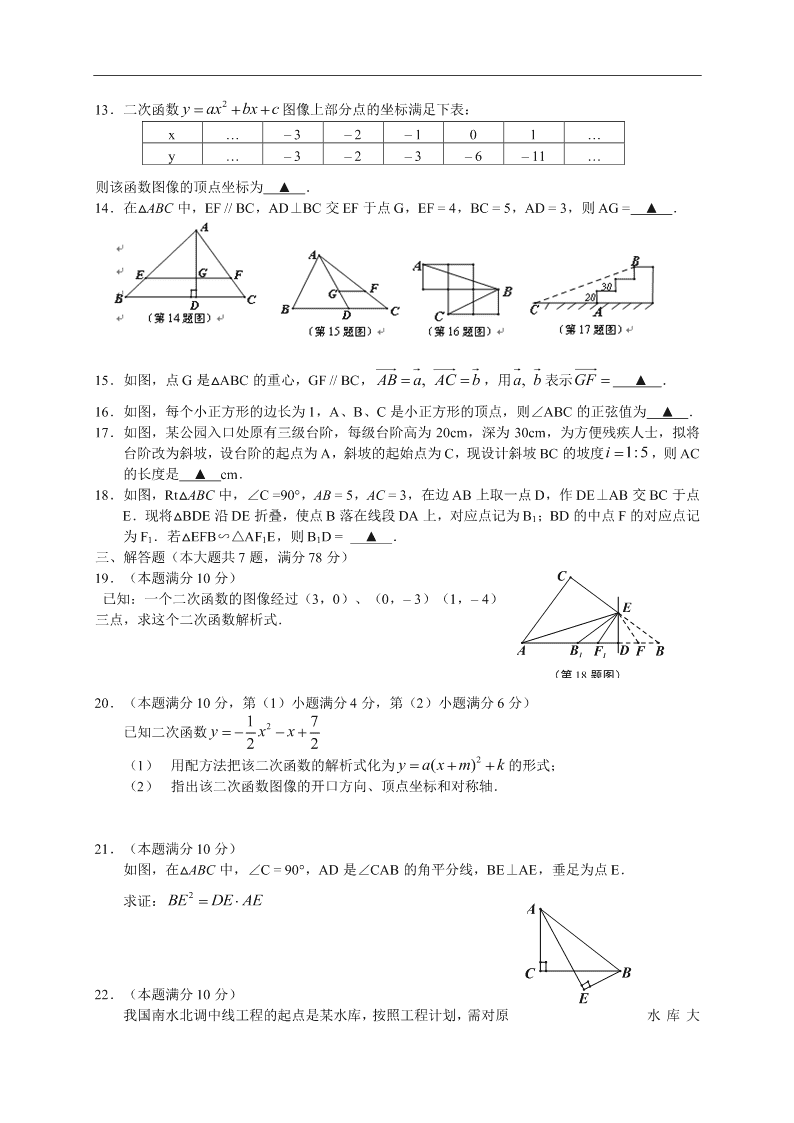13．二次函数 2y ax bx c   图像上部分点的坐标满足下表： x … – 3 – 2 – 1 0 1 … y … – 3 – 2 – 3 – 6 – 11 … 则该函数图像的顶点坐标为 ▲ ． 14．在△ABC 中，EF // BC，AD⊥BC 交 EF 于点 G，EF = 4，BC = 5，AD = 3，则 AG = ▲ ． 15．如图，点 G 是△ABC 的重心，GF // BC， ,AB a AC b，用 ,ab表示GF  ▲ ． 16．如图，每个小正方形的边长为 1，A、B、C 是小正方形的顶点，则∠ABC 的正弦值为 ▲ ． 17．如图，某公园入口处原有三级台阶，每级台阶高为 20cm，深为 30cm，为方便残疾人士，拟将 台阶改为斜坡，设台阶的起点为 A，斜坡的起始点为 C，现设计斜坡 BC 的坡度 1:5i  ，则 AC 的长度是 ▲ cm． 18．如图，Rt△ABC 中，∠C =90°，AB = 5，AC = 3，在边 AB 上取一点 D，作 DE⊥AB 交 BC 于点 E．现将△BDE 沿 DE 折叠，使点 B 落在线段 DA 上，对应点记为 B1；BD 的中点 F 的对应点记 为 F1．若△EFB∽△AF1E，则 B1D = ▲ ． 三、解答题（本大题共 7 题，满分 78 分） 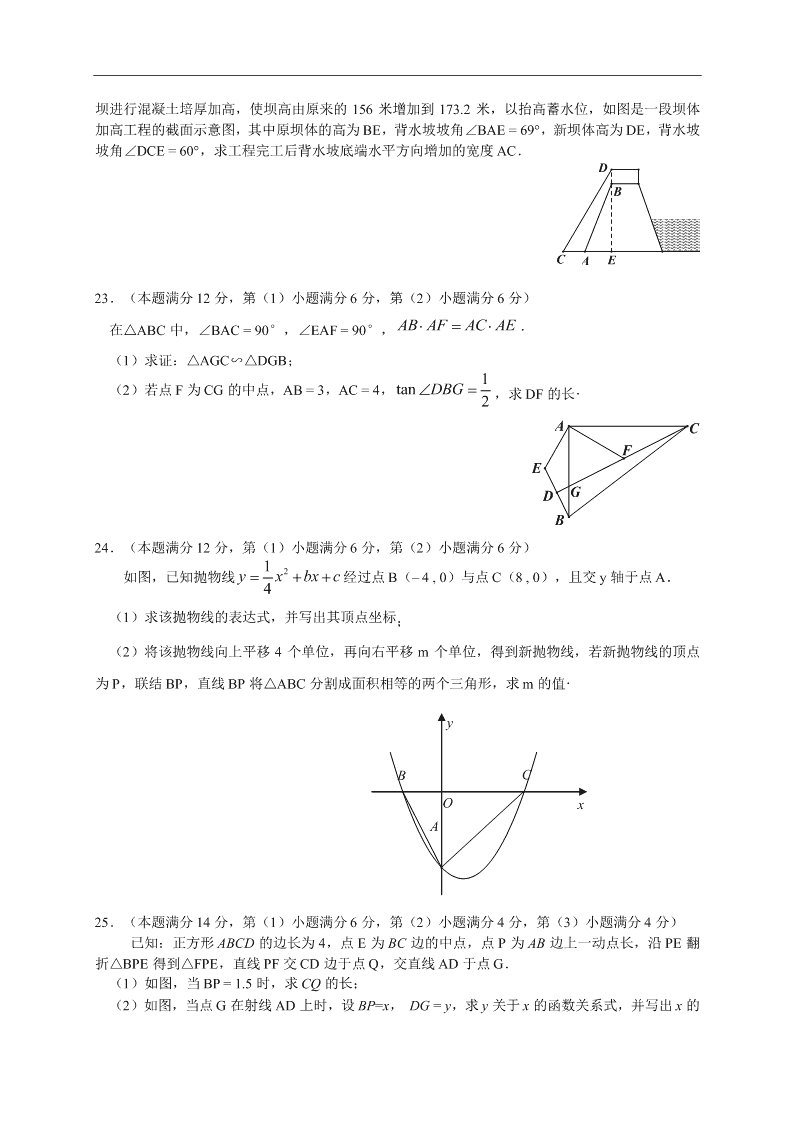19．（本题满分 10 分） 已知：一个二次函数的图像经过（3，0）、（0，– 3）（1，– 4） 三点，求这个二次函数解析式． 20．（本题满分 10 分，第（1）小题满分 4 分，第（2）小题满分 6 分） 已知二次函数 217 22y x x    （1） 用配方法把该二次函数的解析式化为 2()y a x m k   的形式； （2） 指出该二次函数图像的开口方向、顶点坐标和对称轴． 21．（本题满分 10 分） 如图，在△ABC 中，∠C = 90°，AD 是∠CAB 的角平分线，BE⊥AE，垂足为点 E． 求证： 2BE DE AE 22．（本题满分 10 分） 我国南水北调中线工程的起点是某水库，按照工程计划，需对原 水 库 大 （第 18 题图） F1B1 F E D C BA E C B A 坝进行混凝土培厚加高，使坝高由原来的 156 米增加到 173.2 米，以抬高蓄水位，如图是一段坝体 加高工程的截面示意图，其中原坝体的高为 BE，背水坡坡角∠BAE = 69°，新坝体高为 DE，背水坡 坡角∠DCE = 60°，求工程完工后背水坡底端水平方向增加的宽度 AC． E D C B A 23．（本题满分 12 分，第（1）小题满分 6 分，第（2）小题满分 6 分） 在△ABC 中，∠BAC = 90°，∠EAF = 90°， AB AF AC AE   ． （1）求证：△AGC∽△DGB； （2）若点 F 为 CG 的中点，AB = 3，AC = 4， 1tan 2DBG，求 DF 的长． G F E D C B A 24．（本题满分 12 分，第（1）小题满分 6 分，第（2）小题满分 6 分） 如图，已知抛物线 21 4y x bx c   经过点 B（– 4 , 0）与点 C（8 , 0），且交 y 轴于点 A． （1）求该抛物线的表达式，并写出其顶点坐标； （2）将该抛物线向上平移 4 个单位，再向右平移 m 个单位，得到新抛物线，若新抛物线的顶点 为 P，联结 BP，直线 BP 将△ABC 分割成面积相等的两个三角形，求 m 的值． 25．（本题满分 14 分，第（1）小题满分 6 分，第（2）小题满分 4 分，第（3）小题满分 4 分） 已知：正方形 ABCD 的边长为 4，点 E 为 BC 边的中点，点 P 为 AB 边上一动点长，沿 PE 翻 折△BPE 得到△FPE，直线 PF 交 CD 边于点 Q，交直线 AD 于点 G． （1）如图，当 BP = 1.5 时，求 CQ 的长； （2）如图，当点 G 在射线 AD 上时，设 BP=x， DG = y，求 y 关于 x 的函数关系式，并写出 x 的 B A C O x y 取值范围； （3）延长 EF 交直线 AD 于点 H，若△CQE∽△FHG，求 BP 的长． G Q P F E D CB A E D CB A