广东珠海市斗门区2020年九年级毕业生第一次模拟考试数学试卷 解析版 22页

‎2020年广东省珠海市斗门区中考数学一模试卷 一、选择题（本大题共10小题，每小题3分，共30分）在每小题给出的四个选项中，只有一个是正确的，请将所选选项在答题卡上对应题目选项的答案信息点涂黑.‎ ‎1．（3分）2020的相反数是（　　）‎ A．2020 B． C．﹣2020 D．﹣‎ ‎2．（3分）在下列交通标志中，既是轴对称图形，又是中心对称图形的是（　　）‎ A． B． ‎ C． D．‎ ‎3．（3分）新冠病毒（COVID﹣19）肆虐全球，截止至4月17日，全球约有2180000人感染新冠病毒，将2180000用科学记数法可表示为（　　）‎ A．218×104 B．21.8×105 C．2.18×106 D．0.218×106‎ ‎4．（3分）已知直线y＝x+b经过第一、三、四象限，则b的值可能是（　　）‎ A．﹣1 B．0 C． D．3‎ ‎5．（3分）下列计算正确的是（　　）‎ A．a2+a2＝a4 B．a6÷a2＝a4 ‎ C．（a2）3＝a5 D．（a﹣b）2＝a2﹣b2‎ ‎6．（3分）一组数据2，x，4，3，3的平均数是3，则这组数据的中位数和众数分别是（　　）‎ A．3，3 B．2，3 C．3，4 D．3，2‎ ‎7．（3分）对角线互相平分且垂直的四边形是（　　）‎ A．平行四边形 B．矩形 C．菱形 D．等腰梯形 ‎8．（3分）若关于x的一元二次方程kx2﹣2x+1＝0有两个不相等的实数根，则实数k的取值范围是（　　）‎ A．k＞1 B．k＜1 C．k＞1且k≠0 D．k＜1且k≠0‎ ‎9．（3分）如图，⊙O的直径CD垂直弦AB于点E，且CE＝2，DE＝8，则BE的长为（　　）‎ A．2 B．4 C．6 D．8‎ ‎10．（3分）如图，P为∠AOB内一定点，M、N分别是射线OA、OB上一点，当△PMN周长最小时，∠OPM＝40°，则∠AOB＝（　　）‎ A．40° B．45° C．50° D．55°‎ 二、填空题（本大题共7小题，每小题4分，共28分）请把正确答案填写在题后的横线上.‎ ‎11．（4分）使有意义的x的取值范围是　 　．‎ ‎12．（4分）因式分解：m2﹣4n2＝　 　．‎ ‎13．（4分）若正多边形的一个内角等于150°，则这个正多边形的边数是　 　．‎ ‎14．（4分）有A，B两个黑布袋，A布袋中有两个完全相同的小球，分别标有数字1和2．B布袋中有三个完全相同的小球，分别标有数字﹣1，﹣2和﹣3．小明从A布袋中随机取出一个小球，记录其标有的数字为x，再从B布袋中随机取出一个小球，记录其标有的数字为y，这样就确定点Q的一个坐标为（x，y），点Q落在直线y＝x﹣3上的概率为　 　．‎ ‎15．（4分）计算：＝　 　．‎ ‎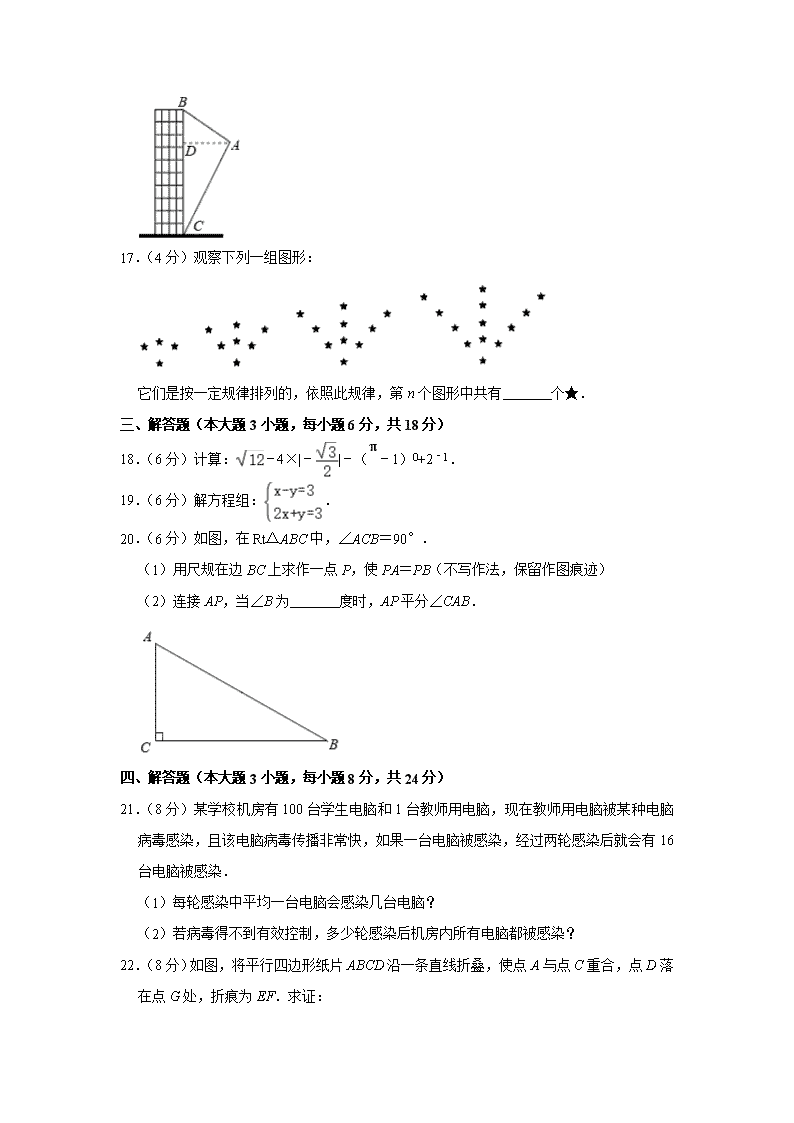16．（4分）如图，航拍无人机从A处测得一幢建筑物顶部B的仰角为30°，测得底部C的俯角为60°，此时航拍无人机与该建筑物的水平距离AD为60米，那么该建筑物的高度BC约为　 　米．‎ ‎17．（4分）观察下列一组图形：‎ 它们是按一定规律排列的，依照此规律，第n个图形中共有　 　个★．‎ 三、解答题（本大题3小题，每小题6分，共18分）‎ ‎18．（6分）计算：﹣4×|﹣|﹣（π﹣1）0+2﹣1．‎ ‎19．（6分）解方程组：．‎ ‎20．（6分）如图，在Rt△ABC中，∠ACB＝90°．‎ ‎（1）用尺规在边BC上求作一点P，使PA＝PB（不写作法，保留作图痕迹）‎ ‎（2）连接AP，当∠B为　 　度时，AP平分∠CAB．‎ 四、解答题（本大题3小题，每小题8分，共24分）‎ ‎21．（8分）某学校机房有100台学生电脑和1台教师用电脑，现在教师用电脑被某种电脑病毒感染，且该电脑病毒传播非常快，如果一台电脑被感染，经过两轮感染后就会有16台电脑被感染．‎ ‎（1）每轮感染中平均一台电脑会感染几台电脑？‎ ‎（2）若病毒得不到有效控制，多少轮感染后机房内所有电脑都被感染？‎ ‎22．（8分）如图，将平行四边形纸片ABCD沿一条直线折叠，使点A与点C重合，点D落在点G处，折痕为EF．求证：‎ ‎（1）∠ECB＝∠FCG；‎ ‎（2）△EBC≌△FGC．‎ ‎23．（8分）如图，平行于y轴的直尺（一部分）与反比例函数y＝（x＞0）的图象交于点A，C，与x轴交于点B，D，连接AC．点A，B的刻度分别为5，2，直尺的宽度BD为2，OB＝2，设直线AC的解析式为y＝kx+b．‎ ‎（1）请结合图象直接写出不等式kx+b＞的解集；‎ ‎（2）求直线AC的解析式；‎ ‎（3）平行于y轴的直线x＝n（2＜n＜4）与AC交于点E，与反比例函数图象交于点F，当这条直线左右平移时，线段EF的长为，求n的值．‎ 五、解答题（本大题2小题，每小题10分，共20分）‎ ‎24．（10分）如图，已知CE是圆O的直径，点B在圆O上由点E顺时针向点C运动（点B不与点E、C重合），弦BD交CE于点F，且BD＝BC，过点B作弦CD的平行线与CE的延长线交于点A．‎ ‎（1）若圆O的半径为2，且点D为弧EC的中点时，求圆心O到弦CD的距离；‎ ‎（2）在（1）的条件下，当DF•DB＝CD2时，求∠CBD的大小；‎ ‎（3）若AB＝2AE，且CD＝12，求△BCD的面积．‎ ‎25．（10分）如图，已知，抛物线y＝x2+bx+c与x轴交于A（﹣1，0），B（4，0）两点，过点A的直线y＝kx+k与该抛物线交于点C，点P是该抛物线上不与A，B重合的动点，过点P作PD⊥x轴于D，交直线AC于点E．‎ ‎（1）求抛物线的解析式；‎ ‎（2）若k＝﹣1，当PE＝2DE时，求点P坐标；‎ ‎（3）当（2）中直线PD为x＝1时，是否存在实数k，使△ADE与△PCE相似？若存在请求出k的值；若不存在，请说明你的理由．‎ ‎2020年广东省珠海市斗门区中考数学一模试卷 参考答案与试题解析 一、选择题（本大题共10小题，每小题3分，共30分）在每小题给出的四个选项中，只有一个是正确的，请将所选选项在答题卡上对应题目选项的答案信息点涂黑.‎ ‎1．（3分）2020的相反数是（　　）‎ A．2020 B． C．﹣2020 D．﹣‎ ‎【分析】直接利用相反数的定义得出答案．‎ ‎【解答】解：2020的相反数是：﹣2020．‎ 故选：C．‎ ‎2．（3分）在下列交通标志中，既是轴对称图形，又是中心对称图形的是（　　）‎ A． B． ‎ C． D．‎ ‎【分析】根据轴对称图形与中心对称图形的概念求解．‎ ‎【解答】解：A、是轴对称图形，不是中心对称图形；‎ B、不是轴对称图形，也不是中心对称图形；‎ C、是轴对称图形，也是中心对称图形；‎ D、是轴对称图形，不是中心对称图形．‎ 故选：C．‎ ‎3．（3分）新冠病毒（COVID﹣19）肆虐全球，截止至4月17日，全球约有2180000人感染新冠病毒，将2180000用科学记数法可表示为（　　）‎ A．218×104 B．21.8×105 C．2.18×106 D．0.218×106‎ ‎【分析】科学记数法表示较大的数形式为a×10n的形式，其中1≤|a|＜10，n为整数，10的指数n比原来的整数位数少1．‎ ‎【解答】解：2180000＝2.18×106，‎ 故选：C．‎ ‎4．（3分）已知直线y＝x+b经过第一、三、四象限，则b的值可能是（　　）‎ A．﹣1 B．0 C． D．3‎ ‎【分析】根据一次函数的性质得出b＜0，再得出选项即可．‎ ‎【解答】解：∵直线y＝x+b经过第一、三、四象限，‎ ‎∴b＜0，‎ ‎∴符合的只有选项A，选项B、C、D都不符合，‎ 故选：A．‎ ‎5．（3分）下列计算正确的是（　　）‎ A．a2+a2＝a4 B．a6÷a2＝a4 ‎ C．（a2）3＝a5 D．（a﹣b）2＝a2﹣b2‎ ‎【分析】直接利用合并同类项、同底数幂的除法、幂的乘方以及完全平方公式的知识求解即可求得答案．‎ ‎【解答】解：A、a2+a2＝2a2，故本选项错误；‎ B、a6÷a2＝a4，故本选项正确；‎ C、（a2）3＝a6，故本选项错误；‎ D、（a﹣b）2＝a2﹣2ab+b2，故本选项错误．‎ 故选：B．‎ ‎6．（3分）一组数据2，x，4，3，3的平均数是3，则这组数据的中位数和众数分别是（　　）‎ A．3，3 B．2，3 C．3，4 D．3，2‎ ‎【分析】根据一组数据2，x，4，3，3的平均数是3，可以求得x的值，从而可以求得这组数据的中位数和众数．‎ ‎【解答】解：∵一组数据2，x，4，3，3的平均数是3，‎ ‎∴2+x+4+3+3＝3×5，‎ 解得，x＝3，‎ ‎∴这组数据是2，3，4，3，3，‎ 按照从小大排列是：2，3，3，3，4，‎ ‎∴这组数据的中位数和众数分别是：3，3，‎ 故选：A．‎ ‎7．（3分）对角线互相平分且垂直的四边形是（　　）‎ A．平行四边形 B．矩形 C．菱形 D．等腰梯形 ‎【分析】根据菱形的判定方法判断即可．‎ ‎【解答】解：对角线互相平分且垂直的四边形是菱形，‎ 故选：C．‎ ‎8．（3分）若关于x的一元二次方程kx2﹣2x+1＝0有两个不相等的实数根，则实数k的取值范围是（　　）‎ A．k＞1 B．k＜1 C．k＞1且k≠0 D．k＜1且k≠0‎ ‎【分析】根据一元二次方程的定义和△的意义得到k≠0且△＞0，即（﹣2）2﹣4×k×1＞0，然后解不等式即可得到k的取值范围．‎ ‎【解答】解：∵关于x的一元二次方程kx2﹣2x+1＝0有两个不相等的实数根，‎ ‎∴k≠0且△＞0，即（﹣2）2﹣4×k×1＞0，‎ 解得k＜1且k≠0．‎ ‎∴k的取值范围为k＜1且k≠0．‎ 故选：D．‎ ‎9．（3分）如图，⊙O的直径CD垂直弦AB于点E，且CE＝2，DE＝8，则BE的长为（　　）‎ A．2 B．4 C．6 D．8‎ ‎【分析】根据CE＝2，DE＝8，得出半径为5，在直角三角形OBE中，由勾股定理得BE．‎ ‎【解答】解：∵CE＝2，DE＝8，‎ ‎∴OB＝5，‎ ‎∴OE＝3，‎ ‎∵AB⊥CD，‎ ‎∴在△OBE中，BE＝＝＝4，‎ 故选：B．‎ ‎10．（3分）如图，P为∠AOB内一定点，M、N分别是射线OA、OB上一点，当△PMN 周长最小时，∠OPM＝40°，则∠AOB＝（　　）‎ A．40° B．45° C．50° D．55°‎ ‎【分析】作P关于OA，OB的对称点P1，P2．连接OP1，OP2．则当M，N是P1P2与OA，OB的交点时，△PMN的周长最短，根据对称的性质可以证得：∠OP1M＝∠OPM＝40°，OP1＝OP2＝OP，根据等腰三角形的性质即可求解．‎ ‎【解答】解：作P关于OA，OB的对称点P1，P2．连接OP1，OP2．则当M，N是P1P2与OA，OB的交点时，△PMN的周长最短，连接P1O、P2O，‎ ‎∵PP1关于OA对称，‎ ‎∴∠P1OP＝2∠MOP，OP1＝OP，P1M＝PM，∠OP1M＝∠OPM＝40°‎ 同理，∠P2OP＝2∠NOP，OP＝OP2，‎ ‎∴∠P1OP2＝∠P1OP+∠P2OP＝2（∠MOP+∠NOP）＝2∠AOB，OP1＝OP2＝OP，‎ ‎∴△P1OP2是等腰三角形．‎ ‎∴∠OP2N＝∠OP1M＝40°，‎ ‎∴∠P1OP2＝180°﹣2×40°＝100°，‎ ‎∴∠AOB＝50°，‎ 故选：C．‎ 二、填空题（本大题共7小题，每小题4分，共28分）请把正确答案填写在题后的横线上.‎ ‎11．（4分）使有意义的x的取值范围是　x≥2　．‎ ‎【分析】当被开方数x﹣2为非负数时，二次根式才有意义，列不等式求解．‎ ‎【解答】解：根据二次根式的意义，得 x﹣2≥0，解得x≥2．‎ ‎12．（4分）因式分解：m2﹣4n2＝　（m+2n）（m﹣2n）　．‎ ‎【分析】先将所给多项式变形为m2﹣（2n）2，然后套用公式a2﹣b2＝（a+b）（a﹣b），再进一步分解因式．‎ ‎【解答】解：m2﹣4n2，‎ ‎＝m2﹣（2n）2，‎ ‎＝（m+2n）（m﹣2n）．‎ ‎13．（4分）若正多边形的一个内角等于150°，则这个正多边形的边数是　12　．‎ ‎【分析】首先根据求出外角度数，再利用外角和定理求出边数．‎ ‎【解答】解：∵正多边形的一个内角等于150°，‎ ‎∴它的外角是：180°﹣150°＝30°，‎ ‎∴它的边数是：360°÷30°＝12．‎ 故答案为：12．‎ ‎14．（4分）有A，B两个黑布袋，A布袋中有两个完全相同的小球，分别标有数字1和2．B布袋中有三个完全相同的小球，分别标有数字﹣1，﹣2和﹣3．小明从A布袋中随机取出一个小球，记录其标有的数字为x，再从B布袋中随机取出一个小球，记录其标有的数字为y，这样就确定点Q的一个坐标为（x，y），点Q落在直线y＝x﹣3上的概率为　　．‎ ‎【分析】先画树状图展示所有6种等可能的结果数，再根据一次函数图象上点的坐标特征，找出点（1，﹣2），（2，﹣1）在直线y＝x﹣3上，然后根据概率公式求解．‎ ‎【解答】解：画树状图为：‎ 共有6种等可能的结果数，其中有（1，﹣2），（2，﹣1）落在直线y＝x﹣3上，‎ 所以点Q落在直线y＝x﹣3上的概率＝＝．‎ 故答案为．‎ ‎15．（4分）计算：＝　1　．‎ ‎【分析】根据同分母分式的加减法法则计算即可．同分母分式相加减，分母不变，分子相加减．‎ ‎【解答】解：‎ ‎＝‎ ‎＝‎ ‎＝‎ ‎＝1．‎ 故答案为：1．‎ ‎16．（4分）如图，航拍无人机从A处测得一幢建筑物顶部B的仰角为30°，测得底部C的俯角为60°，此时航拍无人机与该建筑物的水平距离AD为60米，那么该建筑物的高度BC约为　80　米．‎ ‎【分析】分别利用锐角三角函数关系得出BD，DC的长，进而求出该建筑物的高度．‎ ‎【解答】解：由题意可得：tan30°＝＝＝，‎ 解得：BD＝20（米），‎ tan60°＝＝＝，‎ 解得：DC＝60（米），‎ 故该建筑物的高度为：BC＝BD+DC＝80（米）‎ 故答案为80．‎ ‎17．（4分）观察下列一组图形：‎ 它们是按一定规律排列的，依照此规律，第n个图形中共有　3n+1　个★．‎ ‎【分析】把五角星分成两部分，顶点处的一个不变，其它的分三条线，每一条线上后一个图形比前一个图形多一个，根据此规律找出第n个图形中五角星的个数的关系式．‎ ‎【解答】解：观察发现，第1个图形五角星的个数是：1+3＝4，‎ 第2个图形五角星的个数是：1+3×2＝7，‎ 第3个图形五角星的个数是：1+3×3＝10，‎ 第4个图形五角星的个数是：1+3×4＝13，‎ ‎…‎ 依此类推，第n个图形五角星的个数是：1+3×n＝3n+1．‎ 故答案为：3n+1．‎ 三、解答题（本大题3小题，每小题6分，共18分）‎ ‎18．（6分）计算：﹣4×|﹣|﹣（π﹣1）0+2﹣1．‎ ‎【分析】直接利用负整数指数幂的性质以及绝对值的性质、零指数幂的性质分别化简得出答案．‎ ‎【解答】解：原式＝2﹣2﹣1+‎ ‎＝﹣．‎ ‎19．（6分）解方程组：．‎ ‎【分析】方程组利用加减消元法求出解即可．‎ ‎【解答】解：，‎ ‎①+②得：3x＝6，‎ 解得：x＝2，‎ 把x＝2代入①得：y＝﹣1，‎ 则方程组的解为．‎ ‎20．（6分）如图，在Rt△ABC中，∠ACB＝90°．‎ ‎（1）用尺规在边BC上求作一点P，使PA＝PB（不写作法，保留作图痕迹）‎ ‎（2）连接AP，当∠B为　30　度时，AP平分∠CAB．‎ ‎【分析】（1）运用基本作图方法，中垂线的作法作图，‎ ‎（2）求出∠PAB＝∠PAC＝∠B，运用直角三角形解出∠B．‎ ‎【解答】解：（1）如图，‎ ‎（2）如图，‎ ‎∵PA＝PB，‎ ‎∴∠PAB＝∠B，‎ 如果AP是角平分线，则∠PAB＝∠PAC，‎ ‎∴∠PAB＝∠PAC＝∠B，‎ ‎∵∠ACB＝90°，‎ ‎∴∠PAB＝∠PAC＝∠B＝30°，‎ ‎∴∠B＝30°时，AP平分∠CAB．‎ 故答案为：30．‎ 四、解答题（本大题3小题，每小题8分，共24分）‎ ‎21．（8分）某学校机房有100台学生电脑和1台教师用电脑，现在教师用电脑被某种电脑病毒感染，且该电脑病毒传播非常快，如果一台电脑被感染，经过两轮感染后就会有16台电脑被感染．‎ ‎（1）每轮感染中平均一台电脑会感染几台电脑？‎ ‎（2）若病毒得不到有效控制，多少轮感染后机房内所有电脑都被感染？‎ ‎【分析】（1）设每轮感染中平均一台会感染x台电脑，则第一轮后共有（1+x ‎）台被感染，第二轮后共有（1+x）+x（1+x）即（1+x）2台被感染，利用方程即可求出x的值即可；‎ ‎（2）结合（1）得出n轮后共有（1+x）n台被感染，进而求出即可．‎ ‎【解答】解：（1）设每轮感染中平均每一台电脑会感染x台电脑，依题意得：‎ ‎1+x+（1+x）x＝16，‎ 整理得（1+x）2＝16，‎ 则x+1＝4或x+1＝﹣4，‎ 解得x1＝3，x2＝﹣5（舍去）．‎ 答：每轮感染中平均一台电脑会感染3台电脑；‎ ‎（2）∵n轮后，有（1+x）n台电脑被感染，‎ 故（1+3）n＝4n，‎ ‎∵n＝3时，43＝64，‎ n＝4时，44＝256．‎ 答：4轮感染后机房内所有电脑都被感染．‎ ‎22．（8分）如图，将平行四边形纸片ABCD沿一条直线折叠，使点A与点C重合，点D落在点G处，折痕为EF．求证：‎ ‎（1）∠ECB＝∠FCG；‎ ‎（2）△EBC≌△FGC．‎ ‎【分析】（1）依据平行四边形的性质，即可得到∠A＝∠BCD，由折叠可得，∠A＝∠ECG，即可得到∠ECB＝∠FCG；‎ ‎（2）依据平行四边形的性质，即可得出∠D＝∠B，AD＝BC，由折叠可得，∠D＝∠G，AD＝CG，即可得到∠B＝∠G，BC＝CG，进而得出△EBC≌△FGC．‎ ‎【解答】证明：（1）∵四边形ABCD是平行四边形，‎ ‎∴∠A＝∠BCD，‎ 由折叠可得，∠A＝∠ECG，‎ ‎∴∠BCD＝∠ECG，‎ ‎∴∠BCD﹣∠ECF＝∠ECG﹣∠ECF，‎ ‎∴∠ECB＝∠FCG；‎ ‎（2）∵四边形ABCD是平行四边形，‎ ‎∴∠D＝∠B，AD＝BC，‎ 由折叠可得，∠D＝∠G，AD＝CG，‎ ‎∴∠B＝∠G，BC＝CG，‎ 又∵∠ECB＝∠FCG，‎ ‎∴△EBC≌△FGC（ASA）．‎ ‎23．（8分）如图，平行于y轴的直尺（一部分）与反比例函数y＝（x＞0）的图象交于点A，C，与x轴交于点B，D，连接AC．点A，B的刻度分别为5，2，直尺的宽度BD为2，OB＝2，设直线AC的解析式为y＝kx+b．‎ ‎（1）请结合图象直接写出不等式kx+b＞的解集；‎ ‎（2）求直线AC的解析式；‎ ‎（3）平行于y轴的直线x＝n（2＜n＜4）与AC交于点E，与反比例函数图象交于点F，当这条直线左右平移时，线段EF的长为，求n的值．‎ ‎【分析】（1）结合图象即可写出不等式kx+b＞的解集；‎ ‎（2）由OB与AB的长，及A位于第一象限，确定出A的坐标，将A坐标代入反比例解析式中求出k的值，确定出反比例解析式，由OB+BD求出OD的长，即为C的横坐标，代入反比例解析式中求出CD的长，确定出C坐标，设直线AC解析式为y＝kx+b，将A与C坐标代入求出k与b的值，即可确定出直线AC的解析式；‎ ‎（3）根据题意画出线段EF，根据线段EF的长为，即可求n的值．‎ ‎【解答】解：（1）根据图象可知：‎ 不等式kx+b＞的解集为：2＜x＜4；‎ ‎（2）将A点坐标（2，3）代入y＝，‎ 得：m＝xy＝2×3＝6，‎ ‎∴y＝；‎ 又OD＝4，‎ ‎∴C（4，1.5），‎ 将A（2，3）和C（4，1.5）分别代入y＝kx+b，‎ 得，‎ 解得，‎ ‎∴直线AC的解析式为y＝﹣x+；‎ ‎（3）当x＝n时，点E的纵坐标为﹣n+，‎ 点F的坐标为，依题意，‎ 得：﹣n+﹣＝，‎ 解得n＝或n＝3．‎ 五、解答题（本大题2小题，每小题10分，共20分）‎ ‎24．（10分）如图，已知CE是圆O的直径，点B在圆O上由点E顺时针向点C运动（点B不与点E、C重合），弦BD交CE于点F，且BD＝BC，过点B作弦CD的平行线与CE 的延长线交于点A．‎ ‎（1）若圆O的半径为2，且点D为弧EC的中点时，求圆心O到弦CD的距离；‎ ‎（2）在（1）的条件下，当DF•DB＝CD2时，求∠CBD的大小；‎ ‎（3）若AB＝2AE，且CD＝12，求△BCD的面积．‎ ‎【分析】（1）过O作OH⊥CD于H，根据点D为弧EC的中点，可得∠OCH＝45°，进而得出OH＝CH，再根据圆O的半径为2，即可得到OH＝；‎ ‎（2）先判定△CDF∽△BDC，可得∠DCF＝∠DBC，再根据∠DCF＝45°，即可得出∠DBC＝45°；‎ ‎（3）连接BE，BO，DO，并延长BO至H点，依据∠ABE＝∠OBC＝∠OCB，∠A＝∠A，判定△ABE∽△ACB，即可得到AC＝，设AE＝x，再根据△AOB∽△COH，可得，即，解得x＝5，OH＝4.5，OB＝7.5，即可得到△BCD的面积＝×12×12＝72．‎ ‎【解答】解：（1）如图，过O作OH⊥CD于H，‎ ‎∵点D为弧EC的中点，‎ ‎∴弧ED＝弧CD，‎ ‎∴∠OCH＝45°，‎ ‎∴OH＝CH，‎ ‎∵圆O的半径为2，即OC＝2，‎ ‎∴OH＝；‎ ‎（2）∵当DF•DB＝CD2时，，‎ 又∵∠CDF＝∠BDC，‎ ‎∴△CDF∽△BDC，‎ ‎∴∠DCF＝∠DBC，‎ 由（1）可得∠DCF＝45°，‎ ‎∴∠DBC＝45°；‎ 注：也可以由点D为弧EC的中点，可得弧ED＝弧CD，即可得出∠DCF＝∠DBC＝45°；‎ ‎（3）如图，连接BE，BO，DO，并延长BO至H点，‎ ‎∵BD＝BC，OD＝OC，‎ ‎∴BH垂直平分CD，‎ 又∵AB∥CD，‎ ‎∴∠ABO＝90°＝∠EBC，‎ ‎∴∠ABE＝∠OBC＝∠OCB，‎ 又∵∠A＝∠A，‎ ‎∴△ABE∽△ACB，‎ ‎∴，即AB2＝AE×AC，‎ ‎∴AC＝，‎ 设AE＝x，则AB＝2x，‎ ‎∴AC＝4x，EC＝3x，‎ ‎∴OE＝OB＝OC＝，‎ ‎∵CD＝12，‎ ‎∴CH＝6，‎ ‎∵AB∥CH，‎ ‎∴△AOB∽△COH，‎ ‎∴，即，‎ 解得x＝5，OH＝4.5，OB＝7.5，‎ ‎∴BH＝BO+OH＝12，‎ ‎∴△BCD的面积＝×12×12＝72．‎ ‎25．（10分）如图，已知，抛物线y＝x2+bx+c与x轴交于A（﹣1，0），B（4，0）两点，过点A的直线y＝kx+k与该抛物线交于点C，点P是该抛物线上不与A，B重合的动点，过点P作PD⊥x轴于D，交直线AC于点E．‎ ‎（1）求抛物线的解析式；‎ ‎（2）若k＝﹣1，当PE＝2DE时，求点P坐标；‎ ‎（3）当（2）中直线PD为x＝1时，是否存在实数k，使△ADE与△PCE相似？若存在请求出k的值；若不存在，请说明你的理由．‎ ‎【分析】（1）将点A，B的坐标代入y＝x2+bx+c即可；‎ ‎（2）写出直线AC的解析式，设P（x，x2﹣3x﹣4），则E（x，﹣x﹣1），D（x，0），写出PE，DE的长度，利用PE＝2ED这一等量关系列出方程即可；‎ ‎（3）存在，因为∠AED＝∠PEC，所以要使△ADE与△PCE相似，必有∠EPC＝∠ADE＝90°或∠ECP＝∠ADE＝90°，分两种情况进行讨论，由相似三角形的性质可分别求出k的值．‎ ‎【解答】解：（1）将点A（﹣1，0），B（4，0）代入y＝x2+bx+c，‎ 得，，‎ 解得，，‎ ‎∴抛物线的解析式为y＝x2﹣3x﹣4；‎ ‎（2）当k＝﹣1时，直线AC的解析式为y＝﹣x﹣1，‎ 设P（x，x2﹣3x﹣4），则E（x，﹣x﹣1），D（x，0），‎ 则PE＝|x2﹣3x﹣4﹣（﹣x﹣1）|＝|x2﹣2x﹣3|，DE＝|x+1|，‎ ‎∵PE＝2ED，‎ ‎∴|x2﹣2x﹣3|＝2|x+1|，‎ 当x2﹣2x﹣3＝2（x+1）时，‎ 解得，x1＝﹣1（舍去），x2＝5，‎ ‎∴P（5，6）；‎ 当x2﹣2x﹣3＝﹣2（x+1）时，‎ 解得，x1＝﹣1（舍去），x2＝1，‎ ‎∴P（1，﹣6）；‎ 综上所述，点P的坐标为（5，6）或（1，﹣6）；‎ ‎（3）存在，理由如下；‎ ‎∵∠AED＝∠PEC，‎ ‎∴要使△ADE与△PCE相似，‎ 必有∠EPC＝∠ADE＝90°或∠ECP＝∠ADE＝90°，‎ ‎①当∠EPC＝∠ADE＝90°时，‎ 如图1，CP∥x轴，‎ ‎∵P（1，﹣6），根据对称性可得C（2，﹣6），‎ 将C（2，﹣6），代入直线AC解析式中，‎ 得2k+k＝﹣6，‎ 解得，k＝﹣2；‎ ‎②当∠ECP＝∠ADE＝90°时，‎ 如图2，过C点作CF⊥PD于点F，‎ 则有∠FCP＝∠PEC＝∠AED，‎ 则△PCF∽△AED，‎ ‎∴＝，‎ 在直线y＝kx+k上，当x＝1时，y＝2k，‎ ‎∴E（1，2k），‎ ‎∴DE＝﹣2k，‎ 由，‎ 得或，‎ ‎∴C（k+4，k2+5k），‎ ‎∴F（1，k2+5k），‎ ‎∴CF＝k+3，FP＝k2+5k+6，‎ ‎∴＝，‎ 解得，k1＝k2＝﹣1，k3＝﹣3（此时C与P重合，舍去），‎ 综上，当k＝﹣2或﹣1时，△ADE与△PCE相似．‎