2012年上海初三数学一模试卷及答案(虹口) 8页

虹口区 2011 学年度第一学期初三年级数学学科 期终教学质量监控测试题 （满分 150 分，考试时间 100 分钟） 2012．1 考生注意： 1．本试卷含三个大题，共 25 题； 2．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一 律无效； 3．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或 计算的主要步骤． 一、选择题：（本大题共 6 题，每题 4 分，满分 24 分） [下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸 的相应位置上．] 1．下列二次函数解析式中，其图像与 y 轴的交点在 x 轴下方的是 A． 2 3yx ； B． 2 3yx ； C． 2 3yx   ； D． 2yx ． 2．关于二次函数 221yx   的图像，下列说法中，正确的是 A．开口向上； B．对称轴是直线 1x  ； C．有最高点（0，1）； D．是中心对称图形． 3．在 Rt ABC 中， 90A  ， 5AC  ， 12AB  ，那么sin B 的值是 A． 12 5 ； B． 5 12 ； C． 13 12 ； D． 13 5 ． 4．若 a 、b 均为非零向量，且 a ∥b ，则在下列结论中，一定正确的是 A． ( 0)a mb m； B． ab ； C． ab ； D． ab ． 5．如图，分别以下列选项作为一个已知条件，其中不一定．．．能得到△AOB∽△COD 的是 A．∠BAC=∠BDC； B．∠ABD=∠ACD； C． AO DO CO BO  ； D． AO OD OB CO  ． 6．如图，已知 EF∥CD，DE∥BC，下列结论中，不一定．．．正确是 A． AF AD AD AB  ； B． AE AF AD AC  ； C． DE EF BC CD  ； D． AB AC AD AE  ． 二、填空题：（本大题共 12 题，每题 4 分，满分 48 分） [请将结果直接填入答题纸的相应位置] 7．实数 2 与0.5的比例中项是 ▲ ． 8．抛物线 22( 1) 3yx   的顶点坐标为 ▲ ． A 第 6 题图 B C D E F A B C O D 第 5 题图 C O 第 12 题图 D C B A 9．将抛物线 2 2yx向右平移 4 个单位,再向上平移 3 个单位得到的抛物线表达式是 ▲ ． 10．已知向量 a r 、b r 、x r 满足关系式3( ) 2 0a x b   r r rr ，那么用向量 、 表示向量 x r = ▲ ． 11．已知： 2sin( 15 ) 3 ，则锐角 = ▲ ． 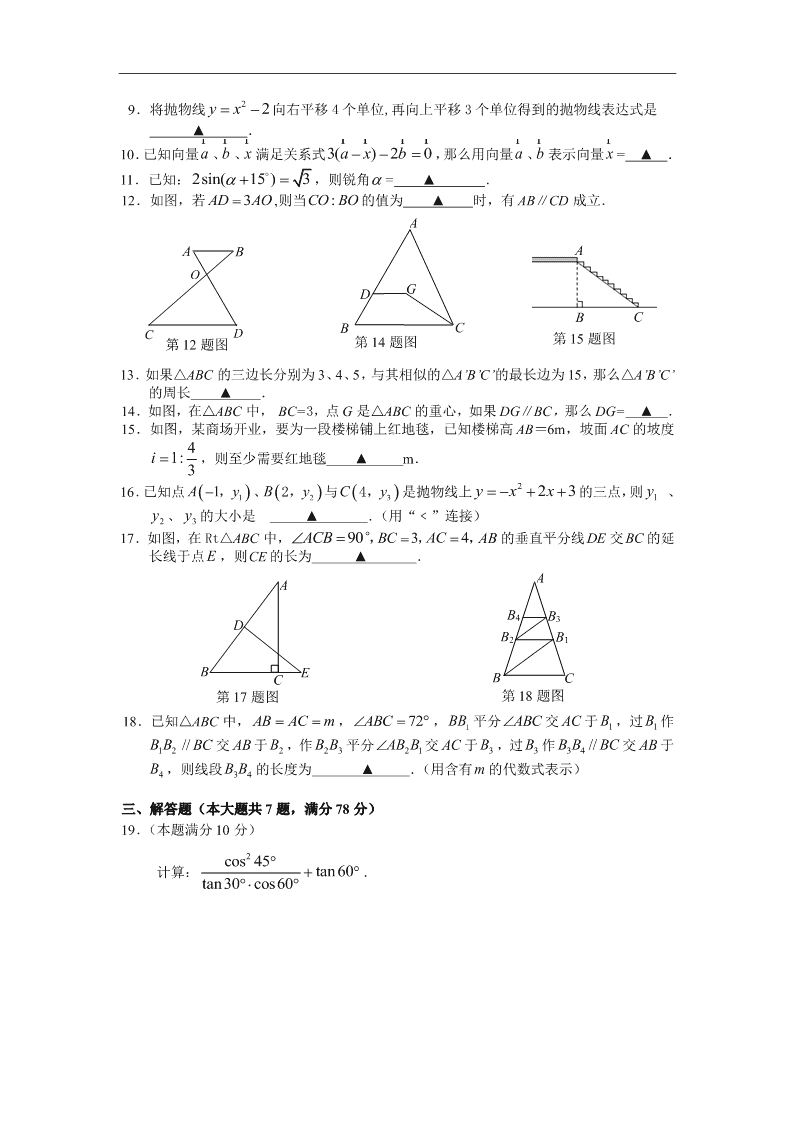12．如图，若 3AD AO ,则当 :CO BO 的值为 ▲ 时，有 AB∥CD 成立． 13．如果△ABC 的三边长分别为 3、4、5，与其相似的△A’B’C’的最长边为 15，那么△A’B’C’ 的周长 ▲ ． 14．如图，在△ABC 中， BC=3，点 G 是△ABC 的重心，如果 DG∥BC，那么 DG= ▲ ． 15．如图，某商场开业，要为一段楼梯铺上红地毯，已知楼梯高 AB＝6m，坡面 AC 的坡度 41: 3i  ，则至少需要红地毯 ▲ m． 16．已知点  11Ay ， 、  2By2， 与  3Cy4， 是抛物线上 2 23y x x    的三点，则 1y 、 2y 、 3y 的大小是 ▲ ．（用“﹤”连接） 17．如图，在 Rt△ABC 中， 90ACB°， 3BC  ， 4AC  ，AB 的垂直平分线 DE 交 BC 的延 长线于点 E ，则CE 的长为 ▲ ． 18．已知△ABC 中， AB AC m， 72ABC ， 1BB 平分 ABC 交 AC 于 1B ，过 1B 作 12BB // BC 交 AB 于 2B ，作 23BB平分 21AB B 交 AC 于 3B ，过 3B 作 34//B B BC 交 AB 于 4B ，则线段 34BB 的长度为 ▲ ．（用含有 m 的代数式表示） 三、解答题（本大题共 7 题，满分 78 分） 19．（本题满分 10 分） 计算： 2cos 45 tan60tan30 cos60    ． A B C 第 15 题图 C G 第 14 题图 D B A C 第 18 题图 B1 B A B2 B3 B4 A D B E C 第 17 题图 D C A E M B 第 23 题图 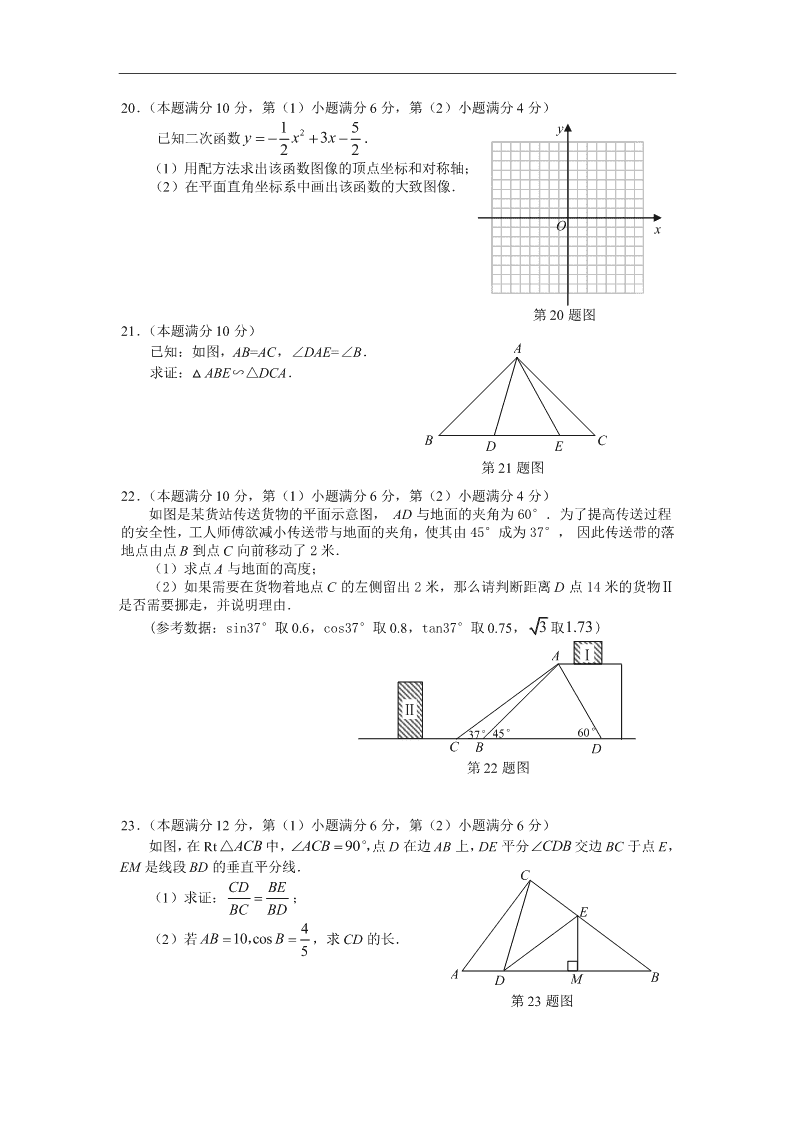20．（本题满分 10 分，第（1）小题满分 6 分，第（2）小题满分 4 分） 已知二次函数 215322y x x    ． （1）用配方法求出该函数图像的顶点坐标和对称轴； （2）在平面直角坐标系中画出该函数的大致图像． 21．（本题满分 10 分） 已知：如图，AB=AC，∠DAE=∠B． 求证：△ ABE∽△DCA． 22．（本题满分 10 分，第（1）小题满分 6 分，第（2）小题满分 4 分） 如图是某货站传送货物的平面示意图， AD 与地面的夹角为 60°．为了提高传送过程 的安全性，工人师傅欲减小传送带与地面的夹角，使其由 45°成为 37°， 因此传送带的落 地点由点 B 到点 C 向前移动了 2 米． （1）求点 A 与地面的高度； （2）如果需要在货物着地点 C 的左侧留出 2 米，那么请判断距离 D 点 14 米的货物Ⅱ 是否需要挪走，并说明理由． (参考数据：sin37°取 0.6，cos37°取 0.8，tan37°取 0.75， 3 取1.73) 23．（本题满分 12 分，第（1）小题满分 6 分，第（2）小题满分 6 分） 如图，在 Rt ACB△ 中， 90ACB°，点 D 在边 AB 上，DE 平分 CDB 交边 BC 于点 E， EM 是线段 BD 的垂直平分线． （1）求证： CD BE BC BD  ； （2）若 410 cos 5 AB B， ，求 CD 的长． A B D E C 第 21 题图 B 第 22 题图 B C 37° A 45° D Ⅱ Ⅰ 60° O y x x 第 20 题图 24．（本题满分 12 分，第（1）小题满分 3 分，第（2）小题满分 4 分，第（1）小题满分 5 分） 如图，在平面直角坐标系 xOy 中，已知抛物线 2y x bx c   经过 (0,3)A ， (1,0)B 两 点，顶点为 M ． （1）求 b 、 c 的值； （2）将 OAB△ 绕点 B 顺时针旋转 90°后，点 A 落到点 C 的位置，该抛物线沿 y 轴上 下平移后经过点C ，求平移后所得抛物线的表达式； （3）设（2）中平移后所得的抛物线与 y 轴的交点为 1A ，顶点为 1M ，若点 P 在平移后 的抛物线上，且满足△ 1PMM 的面积是△ 1PAA 面积的 3 倍，求点 P 的坐标． 25．（本题满分 14 分，第（1）小题满分 4 分，第（2）小题满分 6 分，第（3）小题满分 4 分） 如图，已知梯形 ABCD，AD∥BC，AB＝AD＝5， 3tan 4 DBC．E 为射线 BD 上一动 点，过点 E 作 EF∥DC 交射线 BC 于点 F．联结 EC，设 BE= x， ECF BDC S y S    ． （1）求 BD 的长； （2）当点 E 在线段 BD 上时，求 y 关于 x 的函数关系式，并写出自变量 x 的取值范围； （3）联结 DF，若△ BDF 与△ BDA 相似，试求 BF 的长． B C E F 第 25 题图 A D y x B A O 第 24 题图 M B C A D 备用图 虹口区 2011 学年第一学期初三年级数学学科期终教学质量监控测试卷 参考答案及评分建议 2012.1 说明： 1．解答只列出试题的一种或几种解法．如果考生的解法与所列解法不同，可参照解答 中评分标准相应评分； 2．第一、二大题若无特别说明，每题评分只有满分或零分； 3．第三大题中各题右端所注分数，表示考生正确做对这一步应得分数； 4．评阅试卷，要坚持每题评阅到底，不能因考生解答中出现错误而中断对本题的评 阅．如果考生的解答在某一步出现错误，影响后继部分而未改变本题的内容和难度，视影 响的程度决定后继部分的给分，但原则上不超过后继部分应得分数的一半； 5．评分时，给分或扣分均以 1 分为基本单位． 一、选择题：（本大题共 6 题，每题 4 分，满分 24 分） 1．B ； 2．C ； 3．D ； 4．A； 5．C ； 6．B . 二、填空题：（本大题共 12 题，每题 4 分，满分 48 分） 7． 1 ； 8． (1，3) ； 9． 2( 4) 1yx   ； 10． 2 3ab ； 11．45° ； 12．2 ； 13．36 ； 14．1 ； 15．14 ； 16． 3 1 2yyy； 17． 7 6 ； 18． 3 51 2 m   （或 52mm ） 三、解答题（本大题共 7 题，满分 78 分） 19．（本题满分 10 分） 22()2 +3 31 32 原式＝ ……………………………………………………………………（4 分） 3+ 3 ……………………………………………………………………………（4 分） ＝ 23………………………………………………………………………………（2 分） 20．（本题满分 10 分） 解：（1）经配方得： 2322yx   1（ ） …………………………………………………（2 分） ∴顶点坐标为（3，2），对称轴为直线 3x  ，………………………………（2 分，2 分） （2）画图正确．…………………………………………………………………………（4 分） 21．（本题满分 10 分） 证明：∵AB=AC， ∴ BC   ．……………………………………………………………………（3 分） ∵ BAE BAD DAE     ， CDA BAD B     ， 又 DAE B   ， ∴ BAE CDA   ．……………………………………………………………（5 分） 又∵ ， ∴△ABE∽△DCA．……………………………………………………………（2 分） 22．（本题满分 10 分，第（1）小题满分 6 分，第（2）小题满分 4 分） 解：（1）作 AE⊥BC 于点 E ， ……………………………………………………（1 分） 设 AE x , 在 Rt△ACE 中， 4cot 3CE AE ACE x    ，……………………………………（1 分） 在 Rt△ABE 中， cotBE AE ABE x    ，……………………………………（1 分） ∵BC=CE-BE， 4 23 xx 解得 6x  ．………………………………………………………（2 分） 答：点 A 与地面的高度为 6 米．……………………………………………………（1 分） （2）结论：货物Ⅱ不用挪走． ………………………………………………………（1 分） 在 Rt△ADE 中， 3cot 6 2 33ED AE ADE      ……………………（1 分） cot 8CE AE ACE   …………………………………………………………（1 分） ∴CD=CE+ED=8 2 3 11.46 14 11.46 2.54 2   ……………………………………………………………（1 分） ∴货物Ⅱ不用挪走． 23．（本题满分 12 分，第（1）小题满分 6 分，第（2）小题满分 6 分） （1）证明：∵EM 是线段 BD 的垂直平分线， ∴ED=EB， ∴∠EDB=∠B． ∵DE 平分 CDB ， ∴∠CDE =∠EDB． ∴∠CDE =∠B．……………………………………………………………（2 分） 又∵∠DCE=∠BCD， ∴△CDE∽△CBD．………………………………（1 分） ∴ CD DE BC BD ， 又由 ED=EB， 得 CD BE BC BD ……………………………………………（2 分） （2）解：∵ 90ACB°， 410 cos 5AB B， ∴ 68AC BC， ．…………………………………………………………（1 分） ∵EM 是线段 BD 的垂直平分线， ∴DM=BM ∴ 2 CD BE BE BC BD BM ．………………………………………………………（2 分） ∴ 82 CD BE BM ， 即 4BECD BM …………………………………………（1 分） 4cos 5 BMB BE∴ 5454CD    ．……………………………………（2 分） 24．（本题满分 12 分，第（1）小题满分 3 分，第（2）小题满分 4 分，第（3）小题满分 5 分） 解：（1）已知抛物线 2y x bx c   经过 (0,3) (1,0)AB， ， ∴ 3, 0 1 . c bc      …………………………………………………………………（2 分） 解得 4, 3. b c    ……………………………………………………………………（1 分） ∴ b 、 c 的值分别为-4，3． （2） (0,3)A ， (1,0)B ，∴ 31OA OB， ， 可得旋转后C 点的坐标为(4 1)， ．……………………………………………………（2 分） 当 4x  时，由 2 43y x x   得 3y  ， 可知抛物线 过点(4 3)， ． ∴将原抛物线沿 y 轴向下平移 2 个单位后过点C ． ∴平移后的抛物线解析式为： 2 41y x x   ．…………………………………（2 分） （3） 点 P 在 上，可设 P 点坐标为 2 0 0 0( 4 1)x x x， ， 将 2 41y x x   配方得  223yx   ，其对称轴为 2x  ．……………（1 分） 11 3PMM PAASS△ △ 112MM AA ∴ 0 2x  ． ①当 002x时， ， ∴  00 112 2 3 222xx       ， ∴ 0 1 2x  , 此时 2 00 3414xx    ． ∴ P 点的坐标为 13()24， ．…………………………………………………………（2 分） ②当 0 0x  时，同理可得  00 112 2 3 2 ( )22xx        ， ∴ 0 1x  , 此时 2 004 1 6xx   ． ∴点 P 的坐标为( 1 6) ， ．……………………………………………………………（2 分） 综上述，可知：点 P 的坐标为 或 ． 25．（本题满分 14 分，第（1）小题满分 4 分，第（2）小题满分 6 分，第（3）小题满分 4 分） 解：（1）过点 A 作 AH⊥BD 于点 H, ∵AD∥BC，AB＝AD=5 ∴∠ABD=∠ADB=∠DBC, BH＝HD……………………………………………（1 分） 在 Rt△ABH 中，∵ 3tan tan 4ABD DBC    ， ∴ 4cos 5 BHABD AB   …………………………………………………………(1 分) ∴BH=DH=4， ……………………………………………………………………（1 分） ∴BD=8 ……………………………………………………………………………（1 分） （2）∵EF∥DC ∴ 8FC DE x BF BE x  ， ∵△EFC 与△EFB 同高，∴ 8EFC EFB S FC x S BF x    …………………………………（2 分） 由 EF∥DC 可得：△FEB∽△CDB ∴ 2 22( ) ( )8 64 FEB CDB S BE x x S BD      ……………………………………………………（1 分） ∴ 2 28 1 1 64 64 8 EFC EFC EFB BDC EFB BDC S S S x xy x xS S S x               ，(0 8)x ……（2 分，1 分） （3）∵AD∥BC ∴∠ADB=∠DBC, ∵△ BDF 与△ BDA 相似 ①∠BFD=∠A， 可证四边形 ABFD 是平行四边形 ∴BF=AD=5．…………………………………………………………………………（2 分） ②∠BFD=∠ABD， ∴ DB=DF． 可求得：BF= 64 5 ．……………………………………………………………………（2 分） 综上所述，当△ BDF 与△ BDA 相似时，BF 的长为 5 或 64 5 ．