2011嘉定区中考数学一模试题 5页

2011 年嘉定区九年级第一次质量调研数学试卷 （满分 150 分，考试时间 100 分钟） 考生注意： 1． 本试卷含三个大题，共 25 题； 2． 答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一 律无效； 3． 除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或 计算的主要步骤． 一、选择题：（本大题共 6 题，每题 4 分，满分 24 分） 1．抛物线 12)1( 2  xxky 的开口向上，那么 k 的取值范围是（ ） （A） 0k ； （B） 0k ； （C） 1k ； （D） 0k ． 2．关于抛物线 xxy 22  ，下列说法正确的是（ ） （A）顶点是坐标原点；（B）对称轴是直线 2x ；（ C）有最高点； （D）经过坐标原点． 3．在 Rt△ ABC 中，  90C ，下列等式正确的是（ ） （A） AB BCA sin ； （B） AB ACB cos ； （C） BC ACA tan ；（ D） BC ACB cot ． 4．在等腰△ ABC 中， 4 ACAB ， 6BC ，那么 Bcos 的值是（ ） （A） 5 3 ； （B） 5 4 ； （C） 4 3 ； （D） 3 4 ． 5．已知向量 a ，b ，满足 )4 3(2)(2 1 babx  ，那么 x 等于（ ） （A） ba 24  ； （B） ba 44  ； （C） ba 4 1 ； （D） ba 4 7 ． 6．如图 1，在 Rt△ 中， ， ABDF  ，垂足为 F ， ACDG  ，垂足为G ，交 AB 于点 E ， 5BC ， 12AC ， 2.5DE ，那么 DF 等于（ ） （A） 8.4 ； （B） 6.3 ； （C） 2 ； （D）以上答案都不对． 二、填空题：（本大题共 12 题，每题 4 分，满分 48 分） 【请将结果直接填入答题纸的相应位置】 7．如果抛物线 kxy  2 经过点 )2,1(  ，那么 k 的值是 ． 8．将抛物线 2)1(  xy 向右平移 2 个单位，得到新抛物线的表达式是 ． 9．如果抛物线 2)1( 22  kxxky 与 y 轴的交点为 )1,0( ，那么 k 的值是 ． 10．请你写出一个抛物线的表达式，此抛物线满足对称轴是 y 轴，且在 y 轴的左侧部分是 上升的，那么这个抛物线表达式可以是 ． B C A D E F 图 1 G 11．在 Rt△ ABC 中，  90C ， 8AB ， 4 1cos A ，那么 AC ． 12．如图 2，当小杰沿坡度 5:1i 的坡面由 B 到 A 行走了 26 米时， 小杰实际上升高度 AC 米．（可以用根号表示） 13．在矩形 ABCD 中， BCAB 3 ，点 E 是 DC 的中点，那么 CEBcot ． 14．已知 32 yx  ，那么   yx yx 32 ． 15．如图 3，在△ 中，点 D 在边 AB 上，且 ADBD 2 ，点 E 是 AC 的中点， aBA  ， bAC  ，试用向量 a ，b 表示向量 DE ，那么 DE ． 16．如图 4，在△ 中，点 D 、 E 分别在边 AB 、 AC 的延长线上， BCDE// ， 4AC ， 2:3: BCDE ，那么 AE ． 17．如图 5，在平行四边形 ABCD 中，点 E 是 DC 的中点， BE 与 AC 相交于点O ， 如果△ EOC 的面积是 21cm ，那么平行四边形 的面积是 2cm ． 18．在正方形 ABCD 中，已知 6AB ，点 E 在边CD 上，且 2:1: CEDE ，如图 6． 点 F 在 BC 的延长线上，如果△ ADE 与点C 、 E 、 F 所组成的三角形相似，那么 CF ． 三、解答题：（本大题共 7 题，满分 78 分） 19．（本题满分 10 分） 在平面直角坐标系中，已知一个二次函数的图像经过 )1,1( 、 )4,0(  、 )4,2( 三点． 求这个二次函数的解析式，并写出该图像的对称轴和顶点坐标． 20．（本题满分 10 分） 如图 7，在直角梯形 ABCD 中，  90A ， BCAD // ， 3AD ， 4AB ， 5DC ． 求 BC 的长和 tan C 的值． A C B 图 2 A B D C E 图 3 A B C D E 图 4 A B D C E O 图 5 A B C D E 图 6 A B C D 图 7 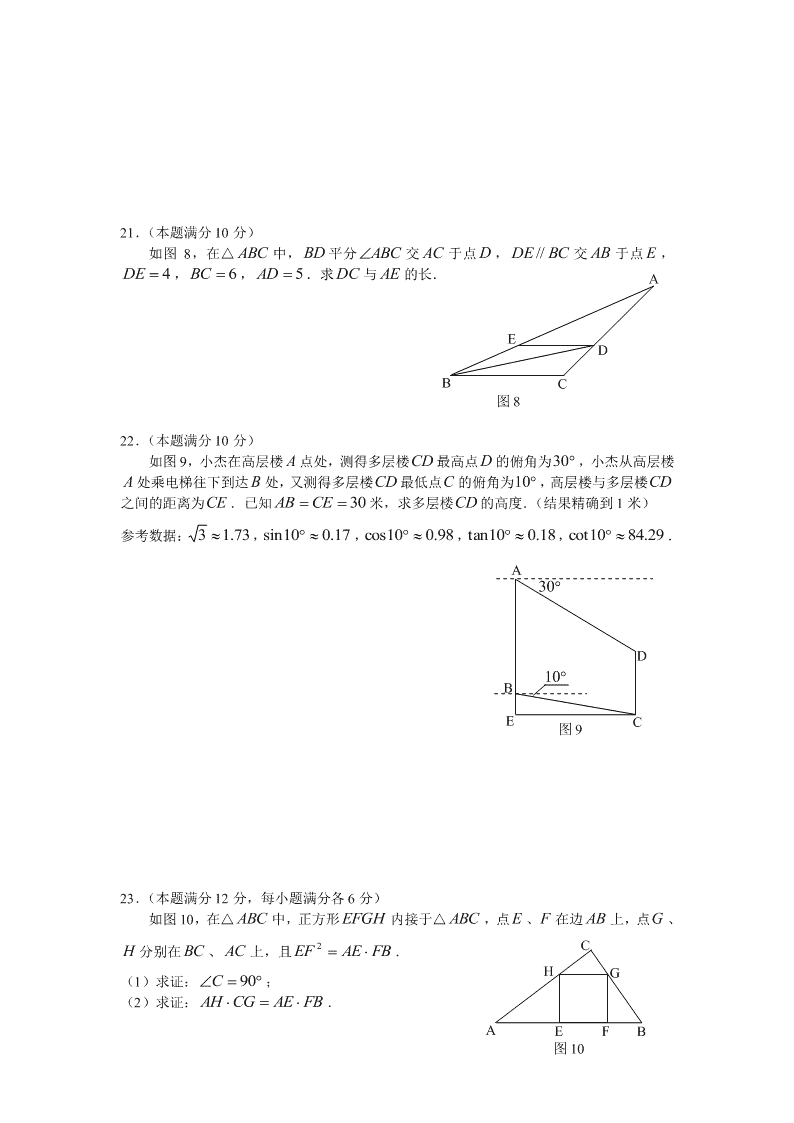21．（本题满分 10 分） 如图 8，在△ ABC 中， BD 平分 ABC 交 AC 于点 D ， BCDE// 交 AB 于点 E ， 4DE ， 6BC ， 5AD ．求 DC 与 AE 的长． 22．（本题满分 10 分） 如图 9，小杰在高层楼 A 点处，测得多层楼CD 最高点 D 的俯角为 30 ，小杰从高层楼 A 处乘电梯往下到达 B 处，又测得多层楼CD 最低点C 的俯角为 10 ，高层楼与多层楼CD 之间的距离为CE ．已知 30 CEAB 米，求多层楼CD 的高度．（结果精确到 1 米） 参考数据： 73.13  ， 17.010sin  ， 98.010cos  ， 18.010tan  ， 29.8410cot  ． 23．（本题满分 12 分，每小题满分各 6 分） 如图 10，在△ 中，正方形 EFGH 内接于△ ，点 E 、F 在边 AB 上，点G 、 H 分别在 BC 、 AC 上，且 FBAEEF 2 ． （1）求证：  90C ； （2）求证： FBAECGAH  ． A E B C D 图 8 C A B E F G 图 10 H C E A B D 10 30 图 9 24．（本题满分 12 分，每小题满分各 4 分） 在平面直角坐标系中，已知点 A 的坐标为 )0,10( ，点 B 在第二象限， 10OB ， 3cot AOB （如图 11），一个二次函数 baxy  2 的图像经过点 A 、 B ． （1）试确定点 B 的坐标； （2）求这个二次函数的解析式； （3）设这个二次函数图像的顶点为C ，△ ABO 绕着点O 按顺 时针方向旋转，点 B 落在 y 轴的正半轴上的点 D ，点 A 落在点 E 上，试求 ECDsin 的值． 25．（本题满分 14 分，第(1)小题满分 5 分，第(2)小题满分 5 分，第(3)小题满分 4 分） 已知在梯形 ABCD 中， DCAB // ， PDAD 2 ， PBPC 2 ， PCDADP  ， 4 PCPD ，如图 12． （1）求证： BCPD // ； （2）若点Q 在线段 PB 上运动，与点 P 不重合，联结CQ 并延长交 DP的延长线于点O ， 如图 13，设 xPQ  ， yDO  ，求 y 与 x 的函数关系式，并写出它的定义域； x y 图 11 A  B O 1 1 -1 -1 （3）若点 M 在线段 PA 上运动，与点 P 不重合，联结CM 交 DP于点 N ，当△ PNM 是 等腰三角形时，求 PM 的值． A P D C B 图 12 A P D C B 图 13 Q O A P D C B 备用图