江苏省盐城市第一初级中学教育集团2012届九年级下学期期中考试 9页

盐城市第一初级中学教育集团2011～2012学年度第二学期期中考试 九年级数学试题 考试时间：120分钟 卷面总分：150分 考试形式：闭卷 ‎ 一、选择题（本大题共有８小题，每小题3分，共24分．在每小题所给出的四个选项中，只有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）‎ ‎1．下列各数中，最大的数是 （ ▲ ）‎ A.－1 B‎.0 ‎C.1 D.‎ ‎2．下列运算正确的是 　 ( ▲ )‎ A． B．‎ C． D．‎ ‎3．已知空气的单位体积质量为‎0.00124 ‎克/厘米3，0.00124用科学记数法表示为（ ▲ ） A．1.24×102 B．1.24×‎103 ‎ C．1.24×10-2 D．1.24×10-3 ‎ ‎4．实数—2、0.3、、、中，无理数的个数是 （ ▲ ）‎ A.2 B‎.3 ‎‎ ‎‎ C.4 D.5‎ ‎5．不等式组的解集在数轴可表示为 （ ▲ ）‎ ‎6．“从一布袋中随机摸出1球恰是黄球的概率为”的意思是 （ ▲ ）‎ ‎ A．摸球5次就一定有1次摸中黄球 ‎ B．摸球5次就一定有4次不能摸中黄球 C．如果摸球次数很多，那么平均每摸球5次就有一次摸中黄球 ‎ D．布袋中有1个黄球和4个别的颜色的球 ‎7．若反比例函数的图象位于第二、四象限内，则m的取值范围是（　▲）‎ A．m＞0 B．m＜‎0 ‎‎ C．m＞1 D．m＜1 ‎ ‎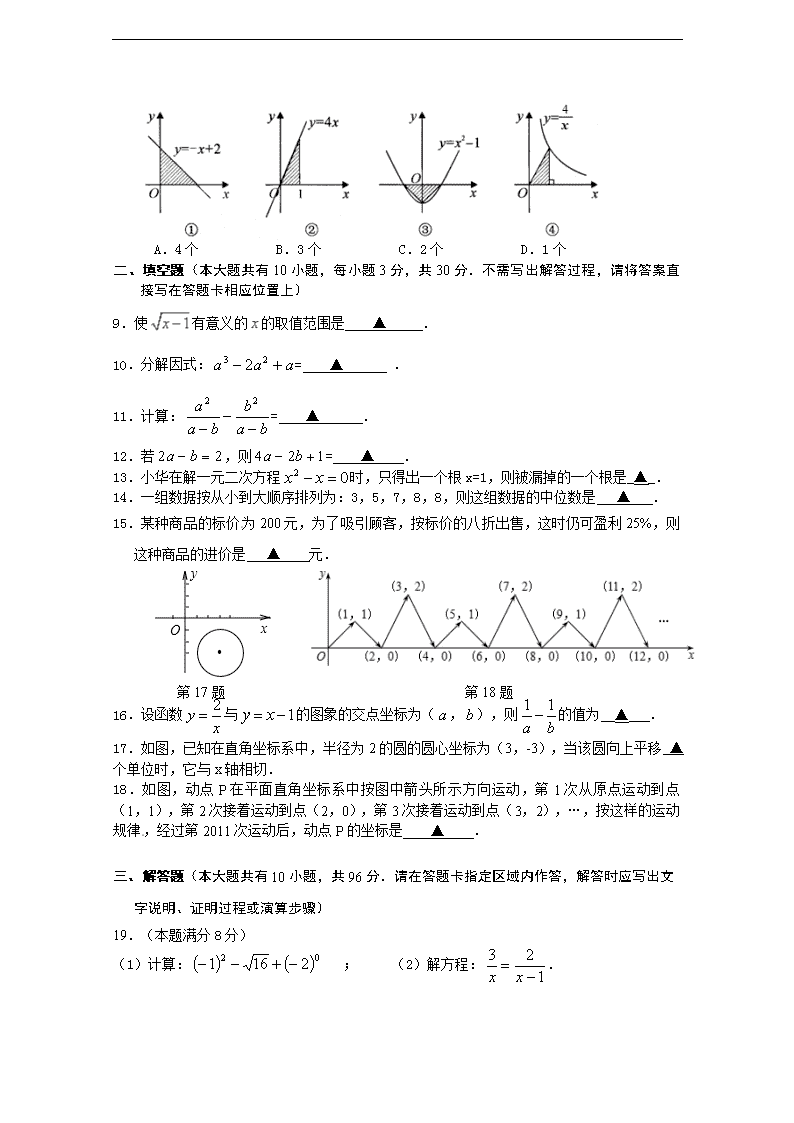8．下列图形中，阴影部分的面积为2的有（　▲　）个[来源:学。科。网Z。X。X。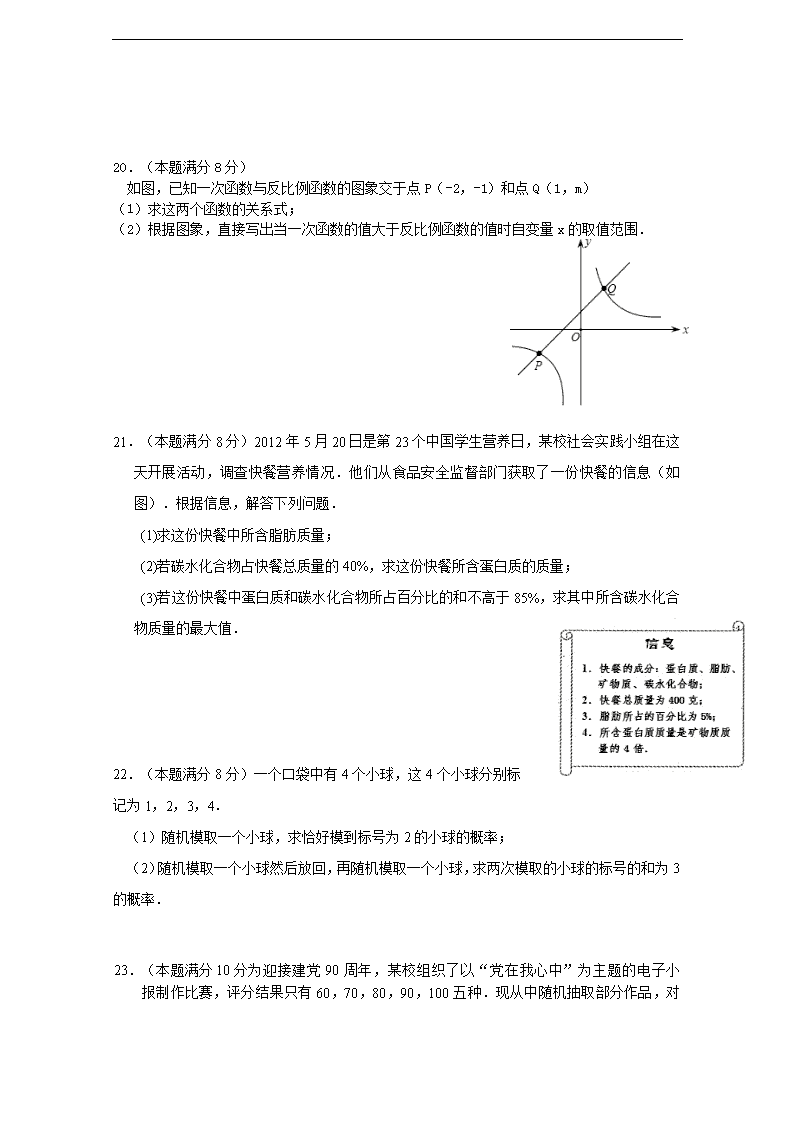K]‎ A．4个 B．3个 C．2个 D．1个 二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请将答案直接写在答题卡相应位置上）‎ ‎9．使有意义的的取值范围是 ▲ ．‎ ‎10．分解因式：= ▲ ．‎ ‎11．计算：= ▲ ．‎ ‎12．若，则= ▲ ．‎ ‎13．小华在解一元二次方程时，只得出一个根x=1，则被漏掉的一个根是_▲_．‎ ‎14．一组数据按从小到大顺序排列为：3，5，7，8，8，则这组数据的中位数是 ▲ ．‎ ‎15．某种商品的标价为200元，为了吸引顾客，按标价的八折出售，这时仍可盈利25%，则这种商品的进价是 ▲ 元．‎ 第17题 第18题 ‎‎ ‎16．设函数与的图象的交点坐标为（，），则的值为__▲___．‎ ‎17．如图，已知在直角坐标系中，半径为2的圆的圆心坐标为（3，-3），当该圆向上平移 ▲ 个单位时，它与x轴相切．‎ ‎18．如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2011次运动后，动点P的坐标是 ▲ ．‎ 三、解答题（本大题共有10小题，共96分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）‎ ‎19．（本题满分8分）‎ ‎（1）计算： ； （2）解方程：．‎ ‎20．（本题满分8分）‎ 如图，已知一次函数与反比例函数的图象交于点P（-2，-1）和点Q（1，m）‎ ‎（1）求这两个函数的关系式；‎ ‎（2）根据图象，直接写出当一次函数的值大于反比例函数的值时自变量x的取值范围．‎ ‎21．（本题满分8分）‎2012年5月20日是第23个中国学生营养日，某校社会实践小组在这天开展活动，调查快餐营养情况．他们从食品安全监督部门获取了一份快餐的信息（如图）．根据信息，解答下列问题．‎ ‎ (1)求这份快餐中所含脂肪质量；‎ ‎ (2)若碳水化合物占快餐总质量的40%，求这份快餐所含蛋白质的质量；‎ ‎ (3)若这份快餐中蛋白质和碳水化合物所占百分比的和不高于85%，求其中所含碳水化合物质量的最大值．[来源:学,科,网]‎ ‎22．（本题满分8分）一个口袋中有4个小球，这4个小球分别标记为1，2，3，4．‎ ‎（1）随机模取一个小球，求恰好模到标号为2的小球的概率；‎ ‎（2）随机模取一个小球然后放回，再随机模取一个小球，求两次模取的小球的标号的和为3的概率．‎ ‎23．（本题满分10分为迎接建党90周年，某校组织了以“党在我心中”为主题的电子小报制作比赛，评分结果只有60，70，80，90，100五种．现从中随机抽取部分作品，对其份数及成绩进行整理，制成如下两幅不完整的统计图．‎ 根据以上信息，解答下列问题：‎ ‎（1）求本次抽取了多少份作品，并补全两幅统计图；‎ ‎（2）已知该校收到参赛作品共900份，请估计该校学生比赛成绩达到90分以上（含90分）的作品有多少份？‎ ‎24．（本题满分10分）如图，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路. 现新修一条路AC到公路l. 小明测量出∠ACD=30º，∠ABD=45º，BC=‎50m. 请你帮小明计算他家到公路l的距离AD的长度（精确到‎0.1m；参考数据：，）.‎ ‎25．（本题满分10分）如图，在△ABC中，∠B=60°，⊙O是△ABC外接圆，过点A作⊙O的切线，交CO的延长线于P点，CP交⊙O于D；‎ ‎（1）求证：AP=AC；‎ ‎（2）若AC=3，求PC的长．‎ ‎[来源:学科网]‎ ‎26．（本题满分10分）某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施.调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台．‎ ‎（1）假设每台冰箱降价x元，商场每天销售这种冰箱的利润是y元，请写出y与x之间的函数表达式；‎ ‎（2）商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？‎ ‎（3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？‎ ‎27．（本题满分12分）在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如，图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.‎ ‎（1）求函数y＝x＋3的坐标三角形的三条边长； ‎ ‎（2）若函数y＝x＋b（b为常数）的坐标三角形周长为16,求此三角形面积.‎ ‎[来源:Zxxk.Com]‎ ‎28．（本题满分12分）‎ 问题情境 已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？‎ 数学模型 设该矩形的长为x，周长为y，则y与x的函数关系式为．‎ 探索研究 ‎⑴我们可以借鉴以前研究函数的经验，先探索函数的图象性质．‎ ① 填写下表，画出函数的图象：‎ x ‎…‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ y ‎…‎ ‎…‎ ② ‎②观察图象，写出该函数两条不同类型的性质；‎ ‎③在求二次函数y=ax2＋bx＋c（a≠‎ ‎0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数(x＞0)的最小值．‎ 解决问题 ‎⑵用上述方法解决“问题情境”中的问题，直接写出答案．‎ 参考答案及评分标准 一、选择题（本大题共有8小题，每小题3分，共24分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 选项 D D[来源:学_科_网Z_X_X_K]‎ D A D C D B 二、填空题（本大题共有10小题，每小题3分，共30分）‎ ‎9． 10． 11． 12．5 13．0 ‎ ‎14．7 15．128 16． 17．1或5 18．（2011，2） ‎ 三、解答题（本大题共有10小题，共96分）‎ ‎19．（本题满分8分）（1）—2 （4分）‎ ‎(2) 3 （8分）‎ ‎20．（本题满分8分）（1），（4分）‎ ‎ （2） 或 （8分）‎ ‎21．（本题满分8分） (1) 20； （2分）‎ ‎ (2)设所含矿物质的质量为x克，由题意得：x+4x+20+400×40% =400，‎ ‎∴x＝44，∴4x＝176‎ 答：所含蛋白质的质量为‎176克． （6分）‎ ‎(3)设所含矿物质的质量为y克，则所含碳水化合物的质量为(380-5y)克，‎ ‎∴4y+(380－5y)≤400×85%，∴y≥40，∴380－5y≤180，‎ ‎∴所含碳水化合物质量的最大值为‎180克． （8分）‎ ‎22．（本题满分8分） （1）； （4分）‎ ‎（2） （8分）‎ ‎23．（本题满分10分）‎ ‎（1）∵24÷20%=120（份），∴本次抽取了120份作品. ‎ 补全两幅统计图 （补全条形统计图2分，扇形统计图2分） ‎ ‎ ‎ ‎（2）∵900×（30%＋10%）=360（份）； ‎ ‎∴估计该校学生比赛成绩达到90分以上（含90分）的作品有360份. （10分）‎ ‎24．（本题满分10分）‎ AD= ‎ ‎25．（本题满分10分）‎ ‎（1）证明过程略； （5分）‎ ‎（2） （10分）‎ ‎26．（本题满分10分）‎ 解：（1）根据题意，得，‎ 即． （ 2分）‎ ‎（2）由题意，得．‎ 整理，得．‎ 解这个方程，得．‎ 要使百姓得到实惠，取．所以，每台冰箱应降价200元． （ 6分）‎ ‎（3）对于，‎ 当时，‎ ‎ ．‎ 所以，每台冰箱的售价降价150元时，商场的利润最大，最大利润是5000元．（ 10分）‎ ‎27．（本题满分12分）‎ ‎(1) ∵ 直线y＝x＋3与x轴的交点坐标为（4,0），与y轴交点坐标为（0,3）， ‎ ‎∴函数y＝x＋3的坐标三角形的三条边长分别为3,4,5. （ 6分）‎ ‎(2) 直线y＝x＋b与x轴的交点坐标为（,0），与y轴交点坐标为（0,b）， ‎ 当b>0时,，得b =4，此时,坐标三角形面积为； ‎ 当b<0时，，得b =－4，此时,坐标三角形面积为. ‎ 综上,当函数y＝x＋b的坐标三角形周长为16时,面积为． （ 12分）‎ ‎28．（本题满分12分）‎ 解⑴①，，，2，，，． （2分）‎ 函数的图象如图． （5分）‎ ‎②本题答案不唯一，下列解法供参考．‎ 当时，随增大而减小；当时,随增大而增大；当时函数的最小值为2． （7分）‎ ‎③‎ ‎=‎ ‎=‎ ‎=‎ 当=0，即时，函数的最小值为2．（10分）‎ ‎⑵当该矩形的长为时，它的周长最小，最小值为． （12分）‎