2008年中考数学分类真理练习24相似三角形 19页

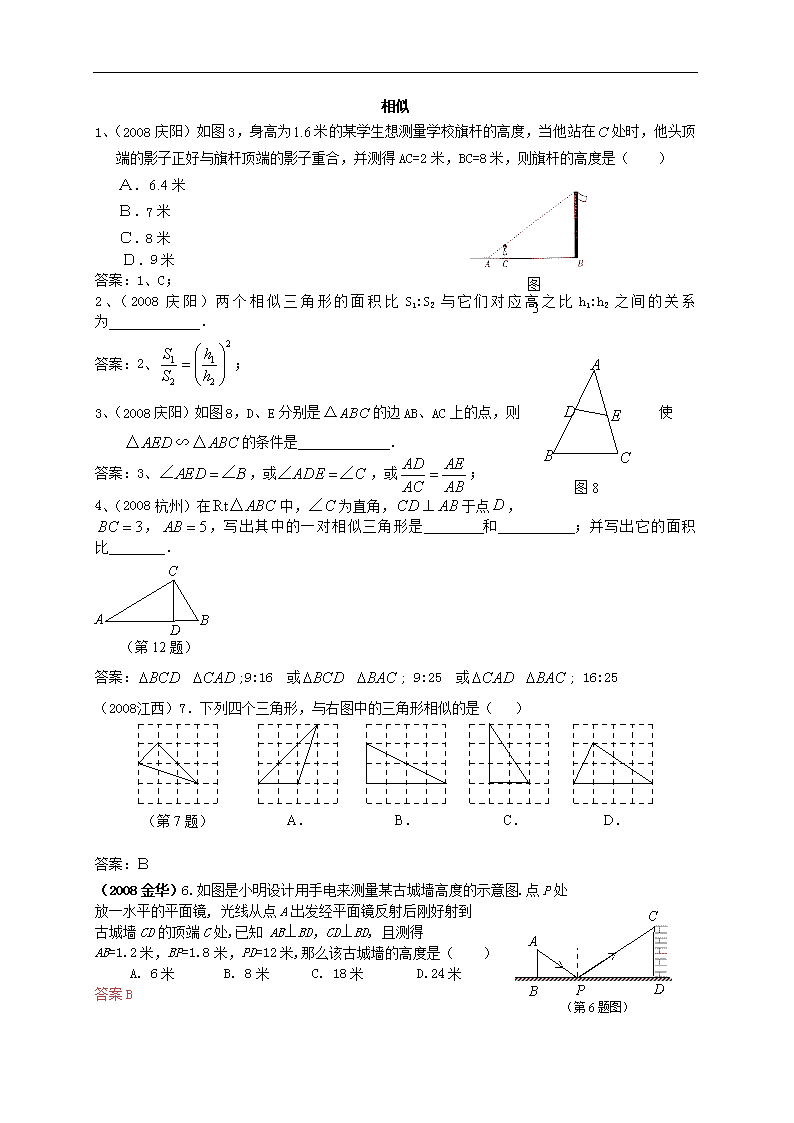
相似 图3‎ ‎1、（2008庆阳）如图3，身高为米的某学生想测量学校旗杆的高度，当他站在处时，他头顶端的影子正好与旗杆顶端的影子重合，并测得AC=‎2米，BC=‎8米，则旗杆的高度是（　　）‎ Ａ．米 Ｂ．‎‎7米 Ｃ．‎‎8米 Ｄ．‎9米 ‎ 答案：1、C；‎ ‎2、（2008庆阳）两个相似三角形的面积比S1:S2与它们对应高之比h1:h2之间的关系为　　 　 　．‎ 图8‎ 答案：2、；‎ ‎3、（2008庆阳）如图8，D、E分别是的边AB、AC上的点，则使∽的条件是 ．‎ 答案：3、，或，或；‎ ‎4、（2008杭州）在中，为直角，于点，，，写出其中的一对相似三角形是 和 ；并写出它的面积比 ．‎ C A B D ‎（第12题）‎ 答案： ;9:16 或 ; 9:25 或 ; 16:25‎ ‎（2008江西）7．下列四个三角形，与右图中的三角形相似的是（ ）‎ ‎（第7题）‎ A．‎ B．‎ C．‎ D．‎ 答案：Ｂ A B P D ‎（第6题图）‎ C C ‎（2008金华）6.如图是小明设计用手电来测量某古城墙高度的示意图.点P处 放一水平的平面镜, 光线从点A出发经平面镜反射后刚好射到 古城墙CD的顶端C处,已知 AB⊥BD，CD⊥BD, 且测得 AB=‎1.2米，BP=‎1.8米，PD=‎12米,那么该古城墙的高度是（ ）‎ A. ‎6米 B. ‎8米 C. ‎18米 D‎.24米 答案B ‎（第16题图）‎ O A1‎ A2‎ A3‎ A4‎ A B B1‎ B2‎ B3‎ ‎1‎ ‎4‎ ‎（2008温州）16．如图，点在射线上，点在射线上，且，．若，‎ 的面积分别为1，4，则图中三个阴影三角形面积之和 为 ．‎ 答案10.5‎ ‎（2008温州）24．如图，在中，，，，分别是边的中点，点从点出发沿方向运动，过点作于，过点作交于，当点与点重合时，点停止运动．设，．‎ ‎（1）求点到的距离的长；‎ ‎（2）求关于的函数关系式（不要求写出自变量的取值范围）；‎ A B C D E R P H Q ‎（第24题图）‎ ‎（3）是否存在点，使为等腰三角形？若存在，请求出所有满足要求的的值；若不存在，请说明理由．‎ 答案（1），，，．‎ 点为中点，．‎ ‎，．‎ ‎，‎ ‎，．‎ ‎（2），．‎ ‎，，‎ ‎，，‎ 即关于的函数关系式为：．‎ ‎（3）存在，分三种情况：‎ A B C D E R P H Q M ‎2‎ ‎1‎ ‎①当时，过点作于，则．‎ ‎，，‎ ‎．‎ ‎，，‎ A B C D E R P H Q ‎，．‎ A B C D E R P H Q ‎②当时，，‎ ‎．‎ ‎③当时，则为中垂线上的点，‎ 于是点为的中点，‎ ‎．‎ ‎，‎ ‎，．‎ 综上所述，当为或6或时，为等腰三角形．‎ ‎（2008 绍兴）将一矩形纸片放在平面直角坐标系中，，，．动点从点出发以每秒1个单位长的速度沿向终点运动，运动秒时，动点从点出发以相等的速度沿向终点运动．当其中一点到达终点时，另一点也停止运动．设点的运动时间为（秒）．‎ ‎（1）用含的代数式表示；‎ ‎（2）当时，如图1，将沿翻折，点恰好落在边上的点处，求点的坐标；‎ 图1‎ O P A x B D C Q y 图2‎ O P A x B C Q y E ‎（3）连结，将沿翻折，得到，如图2．问：与能否平行？与能否垂直？若能，求出相应的值；若不能，说明理由．‎ 解：（1），．‎ 图1‎ O P A x B D C Q y 图2‎ O P A x B C Q y 图3‎ O F A x B C y E Q P ‎（2）当时，过点作，交于，如图1，‎ 则，，‎ ‎，．‎ ‎（3）①能与平行．‎ 若，如图2，则，‎ 即，，而，‎ ‎．‎ ‎②不能与垂直．‎ 若，延长交于，如图3，‎ 则．‎ ‎．‎ ‎．‎ 又，，‎ ‎，‎ ‎，而，‎ 不存在．‎ ‎2008年遵义市27．（14分）如图（1）所示，一张平行四边形纸片，，沿对角线把这张纸片剪成和两个三角形（如图（2）所示）．将沿直线方向平移（点始终在上，与始终保持平行）．当点与重合时停止平移．在平移过程中，与交于点，与交于点．‎ ‎（1）当平移到图（3）的位置时，试判断四边形是什么四边形？并证明你的结论；‎ ‎（2）设平移距离为，四边形的面积为，求与的函数关系式；并求四边形的面积的最大值；‎ D ‎（27题图）‎ A C B A A C F E C 图（1）‎ 图（2）‎ 图（3）‎ ‎（3）连结（请在图（3）中画出），当平移距离的值是多少时，与相似？‎ 解：(1) 四边形B2FD1E是矩形。‎ ‎ 因为△AB1D1平移到图(3)的，所以四边形B2FD1E是一个平行四边形，又因为在平行四边形ABCD中，AB=10，AD=6，BD=8，则有∠ADB是直角。所以四边形B2FD1E是矩形。‎ ‎(2)因为三角形B1B‎2F与三角形AB1D1相似，则有B‎2F==0.6X,B‎1F==0.8x 所以sB2FD1E=B2F×D1F=0.6X × (8-0.8x)=4.8x-0.48x2‎ 即y=4.8x-0.48x2=12-0.48(x-5)‎ 当x=5时，y=12是最大的值。‎ ‎(3)要使△ B1B‎2F与△ B1CF相似，则有 即 解之得：x=3.6‎ ‎（2008太原市）1．下列四个数的绝对值比2大的是（ ）‎ A． B． C．1 D．2‎ 答案：A ‎14．在市政府与国家开发银行山西省分行举行的“百校兴学”工程金融合作签约仪式上，首批项目申请银行贷款3.16亿元．用科学记数法表示3.16亿的结果是 ‎ 答案： ‎ ‎22‎ ‎1‎ ‎3‎ ‎32‎ ‎1‎ ‎5‎ ‎3‎ ‎23‎ ‎3‎ ‎5‎ ‎33‎ ‎7‎ ‎11‎ ‎9‎ ‎24‎ ‎7‎ ‎9‎ ‎34‎ ‎25‎ ‎29‎ ‎27‎ ‎43‎ ‎20．已知，且均为正整数，‎ 如果将进行如下方式的“分解”，那么下列三个叙述：‎ ‎（1）在的“分解”中最大的数是11．‎ ‎（2）在的“分解”中最小的数是13．‎ ‎（3）若的“分解”中最小的数是23，则等于5．‎ 其中正确的是 ．‎ 答案：（2）‎ F E D C B A ‎24. 相似（比例线段，相似多边形，相似三角形）‎ ‎（2008湖北武汉19）.如图，点D，E在BC上，且FD∥AB，FE∥AC.‎ 求证：△ABC∽△FDE．‎ 证明： FD∥AB，FE∥AC B=FDE, C=FED ‎△ABC∽△FDE ‎（2008浙江温州）16．如图，点A1，A2，A3，A4在射线OA上，点B1，B2，B3在射线OB上，且A1B1∥A2B2∥A3B3，A2B1∥A3B2∥A4B3．若△A2B1B2，△A3B2B3的面积分别为1，4，则图中三个阴影三角形面积之和为____________．‎ ‎（第16题图）‎ O A1‎ A2‎ A3‎ A4‎ A B B1‎ B2‎ B3‎ ‎1‎ ‎4‎ 答案：10.5.‎ ‎16．（2008·上海）如果两个相似三角形的相似比是，那么这两个三角形面积的比是 ．‎ 答案：‎ ‎8、（2008·重庆）若△ABC∽△DEF，△ABC与△DEF的相似比为2︰3，则S△ABC︰S△DEF为（）‎ A、2∶3 B、4∶‎9 C、∶ D、3∶2‎ 答案：B ‎17．（2008·上海）如图5，平行四边形中，是边上的点，交于点，如果，那么 ．‎ 答案：‎ ‎25．（2008·上海）已知，，（如图13）．是射线上的动点（点与点不重合），是线段的中点．‎ ‎（1）设，的面积为，求关于的函数解析式，并写出函数的定义域；‎ ‎（2）如果以线段为直径的圆与以线段为直径的圆外切，求线段的长；‎ ‎（3）联结，交线段于点，如果以为顶点的三角形与相似，求线段的长．‎ B A D M E C 图13‎ B A D C 备用图 解：（1）取中点，联结，‎ 为的中点，，． （1分）‎ 又，． （1分）‎ ‎，得； （2分）（1分）‎ ‎（2）由已知得． （1分）‎ 以线段为直径的圆与以线段为直径的圆外切，‎ ‎，即． （2分）‎ 解得，即线段的长为； （1分）‎ ‎（3）由已知，以为顶点的三角形与相似，‎ 又易证得． （1分）‎ 由此可知，另一对对应角相等有两种情况：①；②．‎ ‎①当时，，．．‎ ‎，易得．得； （2分）‎ ‎②当时，，．‎ ‎．又，．‎ ‎，即，得．‎ 解得，（舍去）．即线段的长为2． （2分）‎ 综上所述，所求线段的长为8或2．‎ ‎（济宁市二○○八）26．（12分）‎ 中，，，cm．长为‎1cm的线段在的边上沿方向以‎1cm/s的速度向点运动（运动前点与点重合）．过分别作的垂线交直角边于两点，线段运动的时间为s．‎ ‎（1）若的面积为，写出与的函数关系式（写出自变量的取值范围）；‎ ‎（2）线段运动过程中，四边形有可能成为矩形吗？若有可能，求出此时的值；若不可能，说明理由；‎ ‎（3）为何值时，以为顶点的三角形与相似？‎ 答案：解：（1）当点在上时，，．‎ ‎． 2分 当点在上时，．‎ ‎． 4分 ‎（2），．．‎ ‎． 6分 由条件知，若四边形为矩形，需，即，‎ ‎．‎ 当s时，四边形为矩形． 8分 ‎（3）由（2）知，当s时，四边形为矩形，此时，‎ ‎． 9分 除此之外，当时，，此时．‎ ‎，．． 10分 ‎，．‎ 又，． 11分 ‎，．‎ 当s或s时，以为顶点的三角形与相似． 12分 ‎(2008福州市)‎ ‎12．如图，在中，分别是的中点，若，则的长是 ．‎ ‎（第12题）‎ A B C E D 答案10‎ 21．（本题满分13分）‎ 如图，已知△ABC是边长为6cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q到达点C时，P、Q两点都停止运动，设运动时间为t（s），解答下列问题：‎ ‎（1）当t＝2时，判断△BPQ的形状，并说明理由；‎ ‎（2）设△BPQ的面积为S（cm2），求S与t的函数关系式；‎ ‎（3）作QR//BA交AC于点R，连结PR，当t为何值时，△APR∽△PRQ？‎ ‎（第21题）‎ 解：（1）是等边三角形．‎ 当时．．‎ ‎．‎ ‎．‎ 又，‎ 是等边三角形．‎ ‎（2）过作，垂足为．‎ 由，得．‎ 由，得．‎ ‎．‎ ‎（3），‎ ‎．‎ 又，‎ 是等边三角形．‎ ‎．‎ ‎，‎ ‎，‎ ‎．‎ 四边形是平行四边形．‎ ‎．‎ 又，‎ ‎．‎ ‎，‎ ‎．‎ ‎，即．‎ 解得．‎ 当时，。‎ ‎（2008年贵阳市）6．如果两个相似三角形的相似比是，那么它们的面积比是（B ）‎ A． B． C． D．‎ 第二十五类：曲线运算，函数运算（综合题目）‎ ‎（2008深圳）1、如图9，在平面直角坐标系中，二次函数的图象的顶点为D点，‎ 与y轴交于C点，与x轴交于A、B两点， A点在原点的左侧，B点的坐标为（3，0），‎ OB＝OC ，tan∠ACO＝．‎ ‎（1）求这个二次函数的表达式．‎ ‎（2）经过C、D两点的直线，与x轴交于点E，在该抛物线上是否存在这样的点F，使以点A、C、E、F为顶点的四边形为平行四边形？若存在，请求出点F的坐标；若不存在，请说明理由．‎ ‎（3）若平行于x轴的直线与该抛物线交于M、N两点，且以MN为直径的圆与x轴相切，求该圆半径的长度．‎ ‎（4）如图10，若点G（2，y）是该抛物线上一点，点P是直线AG下方的抛物线上一动点，当点P运动到什么位置时，△APG的面积最大？求出此时P点的坐标和△APG的最大面积.‎ ‎ ‎ 答案：（1）方法一：由已知得：C（0，－3），A（－1，0） ‎ 将A、B、C三点的坐标代入得 ‎ 解得： ‎ 所以这个二次函数的表达式为： ‎ 方法二：由已知得：C（0，－3），A（－1，0） ‎ 设该表达式为： ‎ 将C点的坐标代入得： ‎ 所以这个二次函数的表达式为： ‎ ‎（注：表达式的最终结果用三种形式中的任一种都不扣分）‎ ‎（2）方法一：存在，F点的坐标为（2，－3） ‎ 理由：易得D（1，－4），所以直线CD的解析式为：‎ ‎∴E点的坐标为（－3，0） ‎ 由A、C、E、F四点的坐标得：AE＝CF＝2，AE∥CF ‎∴以A、C、E、F为顶点的四边形为平行四边形 ‎∴存在点F，坐标为（2，－3） ‎ 方法二：易得D（1，－4），所以直线CD的解析式为：‎ ‎∴E点的坐标为（－3，0） ‎ ‎∵以A、C、E、F为顶点的四边形为平行四边形 ‎∴F点的坐标为（2，－3）或（―2，―3）或（－4，3） ‎ 代入抛物线的表达式检验，只有（2，－3）符合 ‎∴存在点F，坐标为（2，－3） ‎ ‎（3）如图，①当直线MN在x轴上方时，设圆的半径为R（R>0），则N（R+1，R），‎ 代入抛物线的表达式，解得 ‎ ‎②当直线MN在x轴下方时，设圆的半径为r（r>0），‎ 则N（r+1，－r），‎ 代入抛物线的表达式，解得 ‎ 圆的半径为或． ‎ ‎（4）过点P作y轴的平行线与AG交于点Q，‎ 易得G（2，－3），直线AG为．‎ 设P（x，），则Q（x，－x－1），PQ．‎ ‎ ‎ 当时，△APG的面积最大 此时P点的坐标为，． ‎ ‎（2008广州）2、如图8，一次函数的图象与反比例函数的图象相交于A、B两点 ‎（1）根据图象，分别写出A、B的坐标；‎ ‎（2）求出两函数解析式；‎ ‎（3）根据图象回答：当为何值时，‎ 一次函数的函数值大于反比例函数的函数值 图8‎ 答案：（1）y＝0.5x＋１，y＝‎ ‎（2）－６4‎ ‎（2008广州）3、如图11，在梯形ABCD中，AD∥BC，AB=AD=DC=‎2cm，BC=‎4cm，在等腰△PQR中，∠QPR=120°，底边QR=‎6cm，点B、C、Q、R在同一直线l上，且C、Q两点重合，如果等腰△PQR以‎1cm/秒的速度沿直线l箭头所示方向匀速运动，t秒时梯形ABCD与等腰△PQR重合部分的面积记为S平方厘米 ‎（1）当t=4时，求S的值 ‎（2）当，求S与t的函数关系式，并求出S的最大值 图11‎ 答案：（1）t＝4时,Q与B重合，P与D重合，‎ 重合部分是＝‎ ‎(2)当 QB=DP=t-4,CR=6-t,AP=6-t 由∽∽‎ 得 ‎,‎ S＝‎ 当t取5时，最大值为 当t取6时，有最大值 综上所述，最大值为 ‎20．(08荆门)如图14，正方形ABCD和正方形OEFG中，点A和点F的坐标分别为(3，2)，(－1，－1)，则两个正方形的位似中心的坐标是______．(1，0)或(－5，－2)‎ 图14‎ ‎12．(08泰州)在平面上，四边形的对角线与相交于，且满足．有下列四个条件：（1）；（2）；（3）；（4）．若只增加其中的一个条件，就一定能使成立，这样的条件可以是（ ）D A．（2）、（4） B．（2） C．（3）、（4） D．（4）‎ ‎1、（5T）（2008湖北省黄冈市，3分）如图，和都是边长为2的等边三角形，点在同一条直线上，连接，则的长为 ．‎ 7．（08南京）小刚身高1.7m，测得他站立在阳光下的影子长为0.85m，紧接着他把手臂竖直举起，测得影子长为1.1m，那么小刚举起的手臂超出头顶（ A ）‎ A．0.5m B．0.55m C．0.6m D．2.2m ‎（第14题图）‎ ‎14．（08连云港）如图，一落地晾衣架两撑杆的公共点为，cm，cm．若撑杆下端点所在直线平行于上端点所在直线，且cm，则 ‎60 cm．‎ O P A 第16题图 ‎[2008年福建省宁德市]16.如图，PA切半圆O于A点，如果∠P＝35°，那么∠AOP＝_____55°.‎ ‎[2008年福建省宁德市]23．（本题满分10分）在边长为1的正方形网格中，有形如帆船的图案①和半径为2的⊙P．‎ ‎⑴将图案①进行平移，使A点平移到点E，画出平移后的图案；‎ ‎⑵以点M为位似中心，在网格中将图案①放大2倍，画出放大后的图案，并在放大后的图案中标出线段AB的对应线段CD；‎ ‎⑶在⑵所画的图案中，线段CD被⊙P所截得的弦长为______．（结果保留根号）‎ M A E B P ‎①‎ ‎23.解：⑴平移后的图案，如图所示；⑵放大后的图案，如图所示；‎ M A E B P D C ‎⑶线段CD被⊙P所截得的弦长为.‎ A C Q D P B ‎（第26题）‎ ‎（2008苏州）如图，在等腰梯形中，，，，．动点从点出发沿以每秒1个单位的速度向终点运动，动点从点出发沿以每秒2个单位的速度向点运动．两点同时出发，当点到达点时，点随之停止运动．‎ ‎（1）梯形的面积等于 ；‎ ‎（2）当时，点离开点的时间等于 秒；‎ ‎（3）当三点构成直角三角形时，点离开点多少时间？‎ 解：（1）36；（2）秒；‎ ‎（3）当三点构成直角三角形时，有两种情况：‎ ‎①当时，设点离开点秒，‎ A C Q D P B E 作于，．‎ ‎，，．‎ 当时，点离开点秒．‎ ‎②当时，设点离开点秒，‎ A C D P B Q E ‎，．‎ ‎．‎ ‎．．．‎ 当时，点离开点秒．‎ 由①②知，当三点构成直角三角形时，点离开点秒或秒．‎ ‎（2008年江苏省无锡市，20T，6分）如图，已知是矩形的边上一点，于，试说明：．‎ ‎20．解法一：矩形中，，， （2分）‎ ‎． （4分）‎ ‎，，． （5分）‎ ‎． （6分）‎ 解法二：矩形中，． （2分）‎ ‎，，． （4分）‎ ‎（下同）‎ ‎（2008年江苏省南通市，17T，4分）已知△ABC和△A′B′C′是位似图形. △A′B′C′的面积6cm2，周长是△ABC的一半.AB＝8cm，则AB边上的高等于（ ）‎ A．3cm B．6cm C．9cm D．12cm答案17．B ‎ ‎（2008年江苏省南通市，26T，12分）如图，四边形ABCD中，AD＝CD，∠DAB＝∠ACB＝90°，过点D作DE⊥AC，垂足为F，DE与AB相交于点E.‎ ‎（1）求证：AB·AF＝CB·CD ‎（2）已知AB＝15cm，BC＝9cm，P是射线DE上的动点.设DP＝xcm（x＞0），四边形BCDP的面积为ycm2.‎ ‎①求y关于x的函数关系式；‎ ‎②当x为何值时，△PBC的周长最小，并求出此时y的值.‎ ‎26.（1）证明：∵AD＝CD，DE⊥AC，∴DE垂直平分AC ‎∴AF＝CF，∠DFA＝DFC＝90°，∠DAF＝∠DCF.‎ ‎∵∠DAB＝∠DAF＋∠CAB＝90°，∠CAB＋∠B＝90°，∴∠DCF＝∠DAF＝∠B 在Rt△DCF和Rt△ABC中，∠DFC＝∠ACB＝90°，∠DCF＝∠B ‎∴△DCF∽△ABC ‎∴，即.∴AB·AF＝CB·CD ‎（2）解：①∵AB＝15，BC＝9，∠ACB＝90°，‎ ‎∴AC＝＝＝12，∴CF＝AF＝6‎ ‎∴×6＝3x＋27（x＞0）‎ ‎②∵BC＝9（定值），∴△PBC的周长最小，就是PB＋PC最小.由（1）可知，点C关于直线DE的对称点是点A，∴PB＋PC＝PB＋PA，故只要求PB＋PA最小.‎ 显然当P、A、B三点共线时PB＋PA最小.此时DP＝DE，PB＋PA＝AB.‎ 由（1），∠ADF＝∠FAE，∠DFA＝∠ACB＝90°，地△DAF∽△ABC.‎ EF∥BC，得AE＝BE＝AB＝，EF＝.‎ ‎∴AF∶BC＝AD∶AB，即6∶9＝AD∶15.∴AD＝10.‎ Rt△ADF中，AD＝10，AF＝6，∴DF＝8.‎ ‎∴DE＝DF＋FE＝8＋＝.‎ ‎∴当x＝时，△PBC的周长最小，此时y＝‎ ‎24. 相似（比例线段，相似多边形，相似三角形）‎ ‎（2008青海）C A BA DA OA EA FA 第18题图 18．如图，是由经过位似变换得到的，点是位似中心，分别是的中点，则与的面积比是（ ）‎ A． B． C． D．‎ 答案：Ｃ